Binary Search | Algorithms - Computer Science Engineering (CSE) PDF Download
Introduction
Given a sorted array arr[] of n elements, write a function to search a given element x in arr[].
A simple approach is to do a linear search. The time complexity of the above algorithm is O(n). Another approach to perform the same task is using Binary Search.
Binary Search: Search a sorted array by repeatedly dividing the search interval in half. Begin with an interval covering the whole array. If the value of the search key is less than the item in the middle of the interval, narrow the interval to the lower half. Otherwise, narrow it to the upper half. Repeatedly check until the value is found or the interval is empty.
Example : The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O(Log n).
The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O(Log n).
We basically ignore half of the elements just after one comparison.
- Compare x with the middle element.
- If x matches with the middle element, we return the mid index.
- Else If x is greater than the mid element, then x can only lie in the right half subarray after the mid element. So we recur for the right half.
- Else (x is smaller) recur for the left half.
Recursive implementation of Binary Search
C++

C

Java

Python3

C#


PHP


Javascript

Output:
Element is present at index 3
Here you can create a check function for easier implementation.
Here is recursive implementation with check function which I feel is a much easier implementation:
C++


Iterative implementation of Binary Search
C++

C

Java
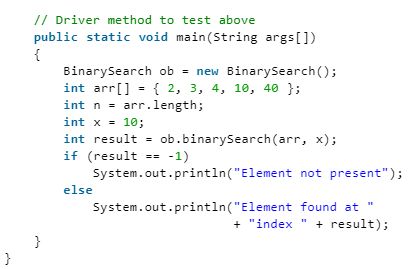
Python3

C#

PHP


Javascript

Output:
Element is present at index 3
Time Complexity: The time complexity of Binary Search can be written as
T(n) = T(n / 2) + c
The above recurrence can be solved either using the Recurrence Tree method or Master method. It falls in case II of the Master Method and the solution of the recurrence is Theta(Logn).
Auxiliary Space: O(1) in case of iterative implementation. In the case of recursive implementation, O(Logn) recursion call stack space.
Algorithmic Paradigm: Decrease and Conquer.
Note: Here we are using
int mid = low + (high – low) / 2;
Maybe, you wonder why we are calculating the middle index this way, we can simply add the lower and higher index and divide it by 2.
int mid = (low + high)/2;
But if we calculate the middle index like this means our code is not 100% correct, it contains bugs.
That is, it fails for larger values of int variables low and high. Specifically, it fails if the sum of low and high is greater than the maximum positive int value(231 – 1 ).
The sum overflows to a negative value and the value stays negative when divided by 2. In java, it throws Array Index Out Of Bound Exception.
int mid = low + (high – low) / 2;
So it’s better to use it like this. This bug applies equally to merge sort and other divide and conquer algorithms.
|
81 videos|113 docs|34 tests
|
FAQs on Binary Search - Algorithms - Computer Science Engineering (CSE)
| 1. What is binary search in computer science engineering? |  |
| 2. How does binary search work? |  |
| 3. What are the advantages of using binary search? |  |
| 4. Can binary search only be used for searching in arrays? |  |
| 5. Are there any limitations of binary search? |  |
















