Binomial Series | Algebra - Mathematics PDF Download
In this final section of this chapter we are going to look at another series representation for a function. Before we do this let’s first recall the following theorem.
Binomial Theorem
If n is any positive integer then,

where,

This is useful for expanding (a+b)n for large n when straight forward multiplication wouldn’t be easy to do. Let’s take a quick look at an example.
Example 1 Use the Binomial Theorem to expand (2x−3)4
Solution. There really isn’t much to do other than plugging into the theorem.

Now, the Binomial Theorem required that n be a positive integer. There is an extension to this however that allows for any number at all.
Binomial Series
If k is any number and |x|<1 then,

So, similar to the binomial theorem except that it’s an infinite series and we must have |x<1 in order to get convergence.
Let’s check out an example of this.
Example 2 Write down the first four terms in the binomial series for √9−x
Solution. So, in this case 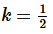 and we’ll need to rewrite the term a little to put it into the form required.
and we’ll need to rewrite the term a little to put it into the form required.
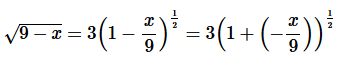
The first four terms in the binomial series is then,

|
161 videos|58 docs
|
FAQs on Binomial Series - Algebra - Mathematics
| 1. What is a binomial series? |  |
| 2. How do you find the coefficients in a binomial series? |  |
| 3. What are some applications of binomial series in mathematics? |  |
| 4. Can the binomial series be used to find the value of irrational numbers? |  |
| 5. Are there any limitations or conditions for the convergence of a binomial series? |  |






















