Blackbody Radiation and Planck's Distribution Law - Thermodynamic and Statistical Physics, CSIR-NET | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
Motivation
- The black body is importance in thermal radiation theory and practice.
- The ideal black body notion is importance in studying thermal radiation and electromagnetic radiation transfer in all wavelength bands.
The black body is used as a standard with which the absorption of real bodies is compared.
Definition of a black body
A black body is an ideal body which allows the whole of the incident radiation to pass into itself ( without reflecting the energy ) and absorbs within itself this whole incident radiation (without passing on the energy). This propety is valid for radiation corresponding to all wavelengths and to all angels of incidence. Therefore, the black body is an ideal absorber of incident radaition.
Black--Body Radiation Laws (1)
1- The Rayleigh-Jeans Law.
- It agrees with experimental measurements for long wavelengths.
- It predicts an energy output that diverges towards infinity as wavelengths grow smaller.
- The failure has become known as the ultraviolet catastrophe.
Ultraviolet Catastrophe
- This formula also had a problem. The problem was the λ term in the denominator.
- For large wavelengths it fitted the experimental data but it had major problems at shorter wavelengths.
Body Radiation Laws (2)
2- Planck Law
- We have two forms. As a function of wavelength.
And as a function of frequency
The Planck Law gives a distribution that peaks at a certain wavelength, the peak shifts to shorter wavelengths for higher temperatures, and the area under the curve grows rapidly with increasing temperature.
Comparison between Classical and Quantum viewpoint
There is a good fit at long wavelengths, but at short wavlengths there is a major disagreement. Rayleigh-Jeans → ∞, but Black-body → 0
Black--Body Radiation Laws (3)
3- Wein Displacement Law
- It tells us as we heat an object up, its color changes from red to orange to white hot.
- You can use this to calculate the temperature of stars.
- The surface temperature of the Sun is 5778 K, this temperature corresponds to a peak emission = 502 nm = about 5000
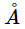 .
. - b is a constant of proportionality, called Wien's displacement constant and equals 2.897 768 5(51) x 10-3 m K = 2.897768 5(51) x 106 nm K.
Black--Body Radiation Laws (4)
4- The Stefan-Boltzmann Law
- Gives the total energy being emitted at all wavelengths by the blackbody (which is the area under the Planck Law curve).
- Explains the growth in the height of the curve as the temperature increases. Notice that this growth is very abrupt
- Sigma = 5.67 * 10-8 J s-1 m-2 K-4, Known as the Stefan- Boltzmann constant.
Black--Body Radiation Laws (5)
Comparison of Rayleigh-Jeans law with Wien's law and Planck's law, for a body of 8 mK temperature.
Application for Black Body
- The area of Earth's disk as viewed from space is, Area = nr2.
- The total energy incident on Earth is, Incident energy = (nr2)So.
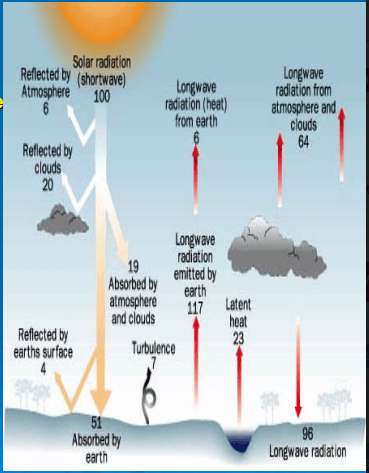
- The energy absorbed by the Earth/atmosphere system, as viewed from space is
Absorbed energy = (nr2)So(1 - A). As we know that bodies must be in radiative equilibrium. The solar energy striking Earth's disk as viewed from space is re-emitted as thermal radiation by the surface of the entire globe, as described by the Stefan-Boltzmann Law, Emitted energy = (4nr2)oT4. - Set the absorbed energy equal to the emitted energy:
(nr2)So(1 - A) = (4nr2)oTE4, Solving for T yields: Te = [S0(1 - A)/(4ct)]<1,4)
= [1370^(1 -0.3)/(4^5.67x10-8)](1,4) = 255 K.
Conclusion
- As the temperature increases, the peak wavelength emitted by the black body decreases.
- As temperature increases, the total energy emitted increases, because the total area under the curve increases.
- The curve gets infinitely close to the x-axis but never touches it.
Summary
- A black body is a theoretical object that absorbs 100% of the radiation that hits it. Therefore it reflects no radiation and appears perfectly black.
- Roughly we can say that the stars radiate like blackbody radiators. This is important because it means that we can use the theory for blackbody radiators to infer things about stars.
- At a particular temperature the black body would emit the maximum amount of energy possible for that temperature.
- Blackbody radiation does not depend on the type of object emitting it. Entire spectrum of blackbody radiation depends on only one parameter, the temperature, T.
FAQs on Blackbody Radiation and Planck's Distribution Law - Thermodynamic and Statistical Physics, CSIR-NET - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What is blackbody radiation and how does it relate to Planck's distribution law? |  |
| 2. How is blackbody radiation explained by thermodynamics and statistical physics? |  |
| 3. What are the applications of blackbody radiation and Planck's distribution law? |  |
| 4. How did Planck's distribution law revolutionize our understanding of physics? |  |
| 5. How does Planck's distribution law explain the phenomenon of ultraviolet catastrophe? |  |
















