Body
Intuitively we understand what a body is. We think that the body is made of a number of particles. Picking up some arbitrary particle we can talk about particles that are on top or below this particle, in front or behind this particle, and to the right or left of this particle. This relationship between the particles is maintained in all motions of the body, that is if two particles is on two different sides of another particle, these two particles stay on either side of the other particle for any motion of the body. Therefore, we say that the body is made up of ordered particles. If the number of particles is countless then the body is described as a continuum and when it is countable it is described to be discrete.
Now, we want to express these intuitive notions of the body in the language of mathematics. The mathematical analogue of the material particle is the point. Mathematically, by point we mean a collection of ‘n’ (real) numbers, for our purposes here. Assuming that we have a scale to measure the distance, then to identify other particles from a given particle, we need to give three distances, namely the distance on top, to the right and in the front of that particular particle. Hence, for each point we have to associate three numbers corresponding to the three distances mentioned above. Therefore the points are said to belong to a three dimensional space, since the value of n is 3. If we use a linear scale, which is the usual practice, to measure the distance then we say that the points belong to a 3D Euclidean space or more specifically 3D Euclidean translation space, also sometimes referred to as 3D Euclidean point space. Further, in the language of mechanics, this mapping of the particles to points in the 3D Euclidean space is called a placer and is denoted by κ.
Though one might understand what a body is intuitively, some choices made here to mathematically represent it needs deliberation. For this we need to understand the mathematical notion of a “point”. Though we associate it as a point. It is not. · is at best a collection of points. Point by definition is a limiting sphere obtained when the radius of the sphere tends to zero. Thus one cannot see a point; its volume is also zero. Stacking of points along one direction alone yields a line, stacking of lines along a direction perpendicular to the direction of the line yields a plane, stacking of planes along the normal direction to the plane yields a 3D cube which alone can be seen and has a volume. Thus, one should realize that by stacking countless number of points of zero volume we have created a finite volume, as a consequence of limiting process. Consequently, the same1 countless number of points could occupy different volumes at different instances in time.
It should be clear from the above discussion that particle is not a chunk of material that many believe it to be. This is because the particle is mapped on to the mathematical idea of a point which as we saw above has zero volume.
| 1When the number of points is countless, using this adjective same is a oxymoron. But it is used to convey an idea. |
Let B denote the abstract body, that is the set of particles that constitute the body. Assuming that the body is made of only 8 particles we write
B = {(X, Y, Z)|X ∈ {0, 1}, Y ∈ {0, 1}, Z ∈ {0, 1}}, (3.1)
meaning that the eight particles are mapped on to the points (0, 0, 0), (1, 0, 0), (1, 1, 0), (0, 1, 0), (0, 0, 1), (1, 0, 1), (1, 1, 1), (0, 1, 1). The right hand side of the equation (3.1) means the following: Take an element each from the set X, Y and Z and form a new set called B which is the collection of these three elements. Mathematically, this is stated as: the set B is obtained by taking the Cartesian product2 of the sets X, Y and Z. The elements in the set X are 0 and 1 and that in the set Y and Z are also 0 and 1. The elements in the set need not be discrete they can be continuous also. In fact, they have to be continuous when the body is a continuum.
Thus, for the body made up of countless number of material particles, we write
B = {(X, Y, Z)|0 ≤ X ≤ 1, 0 ≤ Y ≤ 1, 0 ≤ Z ≤ 1}. (3.2)
By this, we mean that each point within the unit cube is occupied by a material particle belonging to the body. Since the body occupies contiguous region in space it is apt that it is described as a continuum. Pictorially this configuration of the body is represented as shown in figure 3.1a.
It is just incidental that one of the vertex of the cube coincides with the point (0, 0, 0). Another person can map the same body onto a different region of the Euclidean space and thus he might write
B = {(X, Y, Z)|X0 ≤ X ≤ X0+1, Y0 ≤ Y ≤ Y0+1, Z0 ≤ Z ≤ Z0+1}, (3.3)
where, X0, Y0, Z0 are some constants. This representation of the unit cube is shown pictorially in figure 3.1b. In fact, it is not necessary that the cube be oriented such that the normal to its faces coincide with the Cartesian coordinate basis, it can make an angle with the coordinate basis too, as shown in figure 3.1c. This configuration of the body is analytically expressed as:
B = {(X cos(θ) + Y sin(θ) − X0, −X sin(θ) + Y cos(θ) − Y0, Z − Z0)
|0 ≤ X ≤ 1, 0 ≤ Y ≤ 1, 0 ≤ Z ≤ 1}, (3.4)
where, X0, Y0, Z0 and θ are some constants. Before proceeding further, we recap the properties of the placers. First, the placers are one to one functions that is each material particle gets mapped
| 2The Cartesian product of two sets X and Y, denoted X × Y , is the set of all possible ordered pairs whose first component is a member of X and whose second component is a member of Y. |
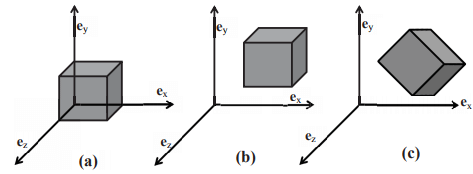
Figure 3.1: Schematic of cube oriented in space such that (a) One of the corners coincides with the origin and the normal to the faces of the cube are oriented parallel to the Cartesian basis (b) None of the corners coincides with the origin but the normal to the faces of the cube are oriented parallel to the Cartesian basis (c) None of the corners coincides with the origin and the normal to the faces of the cube are not oriented parallel to the Cartesian basis on to a unique point in the 3D Euclidean space. However, there is no unique placer for a given body. Different persons can map a given body to different regions of Euclidean point space. We shall later see how this non-uniqueness of placers is built into the theory developed to describe the mechanical response of the bodies.
While defining bodies in equations (3.1) through (3.4) we tacitly assumed that the point space corresponded to Cartesian coordinates. This specification of the coordinate system is important to arrive at the formula to be used to compute the distance between two triplets. Recognize that if we are using the same formula to obtain the distance between two triplets in different coordinate systems, it is equivalent to using different scales to measure the distance.
Many a times, the choice of coordinate system is made so that we can define the body succinctly. For example, consider a body in the shape of an annular (or solid) right circular cylinder of length, H. Using cylindrical polar coordinates, (R, Θ, Z), this body is mathematically defined as:
B = {(R, Θ, Z)|Ri ≤ R ≤ Ro, 0 ≤ Θ ≤ 2π, 0 ≤ Z ≤ H}, (3.5)
where Ri and Ro are some positive constants, with Ri = 0 for a solid cylinder. Try defining this body using Cartesian coordinates.
Experience has shown that it is easier to do computations if we use vector space instead of point space. Naively, while in vector spaces we speak of position vectors of a point, in point space we speak about the coordinates of a point. Next, we would like to establish this relationship between the mathematical ideas of the vector space and point space. To do this, for each ordered pair of points (a, b) in the Euclidean point space E there corresponds a unique vector in the Euclidean vector space,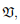 denoted by
denoted by 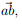 with the properties
with the properties
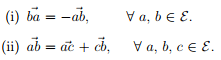
(iii) Choosing arbitrarily a point o from E, and a Cartesian coordinate basis to span the vector space,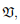 there corresponds to each vector a ∈
there corresponds to each vector a ∈ 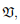 a unique point a ∈
a unique point a ∈ 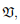 such that a =
such that a = 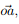 the point o is called the origin and a the position of a relative to o.
the point o is called the origin and a the position of a relative to o.
In other words, property (iii) states that the components of any vector a (a1, a2, a3) relative to a chosen Cartesian coordinate basis correspond to the coordinates of some point a in E. The fact that this holds only for Cartesian coordinate system cannot be overemphasized. To see this, recall that in cylindrical polar coordinate system even though a triplet (R, Θ, Z) characterizes a point in E, position vectors have components of the form (R, 0, Z) only. That is the components of the position vector of a point is not same as the coordinates of the point.
The notions of distance and angle in E are derived from the scalar product on the supporting vector space 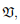 : the distance between the arbitrary points a and b is defined by
: the distance between the arbitrary points a and b is defined by
| 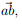 | and the angle, α subtended by a and b at a third arbitrary point c by
| and the angle, α subtended by a and b at a third arbitrary point c by
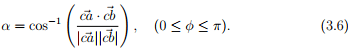
Thus, the choice of scale corresponds to the different expressions for the scalar product.
Considering the physical body to be made up of material particles, denoted by P, we have seen how it can be mapped to the 3D Euclidean poin
space and hence to the 3D Euclidean vector space. Thus, the region occupied by this body in the 3D Euclidean vector space is called as the configuration of the body and is denoted by 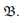 Then, the placing function
Then, the placing function 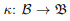 and its inverse κ−1 :
and its inverse κ−1 : 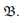 → B are defined as:
→ B are defined as:
X = κ(P), P = κ−1 (X). (3.7)
Recognize that the inverse exist because the mappings are one to one by definition. Henceforth, by placer we mean placing the body in the Euclidean vector space not the point space.
Next, let us understand what time is. Time concerns with the ordering of events. That is, it tells us whether an event occurred before or after a particular event. We shall assume that we cannot count the number of events. Hence, we map the events to the points on a real line. This assumption that the number of events is countless, is required so that we can take derivatives with respect to time. The part of the real line that is used to map a set of events is the prerogative of the person who establishes this correspondence which is similar to the mapping of the body on to the 3D Euclidean point space. The motion of a body is considered to be an event in mechanics. When a body moves, its configuration changes, that is the region occupied by the body in the 3D Euclidean vector space changes.
Let t be a real variable denoting time such that 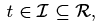 set of reals. If we could associate a configuration, Bt for the body B for each instant of time in the interval of interest then the family of configurations {Bt : t ∈ I} is called motion of B. Hence, we can define functions φ: B × I → Bt and φ−1 : Bt × I → B such that
set of reals. If we could associate a configuration, Bt for the body B for each instant of time in the interval of interest then the family of configurations {Bt : t ∈ I} is called motion of B. Hence, we can define functions φ: B × I → Bt and φ−1 : Bt × I → B such that
x = φ(P, t), P = φ−1 (x, t). (3.8)
In a motion of B a typical particle, P occupies a succession of points which together form a curve in E. This curve is called the path of P and is given in a parametric manner by equation (3.8a). The velocity and acceleration of P are defined as rate of change of position and velocity with time, respectively, as P traverses its path.
While the definition of motion by (3.8a) is satisfactory, it would be useful if it were to be a function of the vectors instead of points. To achieve this we make use of the equation (3.7b). That is we choose a certain configuration of the body and identify the particles by the position vector of the point it occupies in this configuration, then
x = φ(κ−1 (X), t) = χκ (X, t). (3.9)
χκ is called the motion field and the subscript κ denotes that it depends on the configuration which is used to identify the particles. The configuration in which the particles are identified is called the reference configuration and is denoted by Br. This definition does not require the reference configuration to be a configuration actually occupied by the body during its motion. If the reference configuration were to be a configuration actually occupied by the body during its motion at some time to, then (3.9) could be obtained from (3.8) as
x = φ(φ−1 (X, to), t) = χto (X, t). (3.10)
We call χκ (or χto ) the deformation field when it is independent of time or its dependence on time is irrelevant.
Now, we would like to make a few remarks. The definition of a body and motion is independent of whether we are concerned with rigid body or deformable body. However, certain structures or details impounded on the body depends on this choice. Till now, we have been talking about the body being a set of particles but to be precise we should have said material particles. This detail is important within the context of deformable bodies, as we shall see later. It should also be remembered that the distinction that a given particle is steel or wood is made right in the beginning. Thus, within the realms of classical mechanics we cannot model chemically reacting body where material particles of a particular type gets transformed into another. Because the body is considered to be a fixed set of material particles, they cannot die or be born or get transformed.
As we shall see later, an important kinematical quantity in the study of deformable bodies is the gradient of motion. For us to be able to find the gradient of motion, we require the motion field, (3.9) to be continuous on B and there should exist countless material particles of the same type (material) in spheres of radius, r for any value of r less than δo where δo is some constant. It is for this purpose, in the study of deformable bodies we require the body to be a continuum.
denoted by
with the properties
there corresponds to each vector a ∈
a unique point a ∈
such that a =
the point o is called the origin and a the position of a relative to o.
: the distance between the arbitrary points a and b is defined by
| and the angle, α subtended by a and b at a third arbitrary point c by
Then, the placing function
and its inverse κ−1 :
→ B are defined as:
set of reals. If we could associate a configuration, Bt for the body B for each instant of time in the interval of interest then the family of configurations {Bt : t ∈ I} is called motion of B. Hence, we can define functions φ: B × I → Bt and φ−1 : Bt × I → B such that
























