Bonding in Coordination Complexes: Crystal Field Theory | Inorganic Chemistry PDF Download
What is Crystal Field Theory?
Crystal field theory describes
the net change in crystal energy resulting from the orientation of d orbitals of a transition metal cation inside a coordinating group of anions also called ligands.
A major feature of transition metals is their tendency to form complexes. A complex may be considered as consisting of a central metal atom or ion surrounded by a number of ligands. The interaction between these ligands with the central metal atom or ion is subject to crystal field theory.
Crystal field theory was established in 1929 treats the interaction of metal ion and ligand as a purely electrostatic phenomenon where the ligands are considered as point charges in the vicinity of the atomic orbitals of the central atom. Development and extension of crystal field theory taken into account the partly covalent nature of bonds between the ligand and metal atom mainly through the application of molecular orbital theory.
Crystal field theory often termed as ligand field theory.
Overview of Crystal Field TheoryIn order to understand clearly the crystal field interactions in transition metal complexes, it is necessary to have knowledge of the geometrical or spatial disposition of d orbitals. The d-orbitals are fivefold degenerate in a free gaseous metal ion. If a spherically symmetric field of negative ligand filed charge is imposed on a central metal ion, the d-orbitals will remain degenerate but followed by some changes in the energy of free ion.
A summary of the interactions is given below.
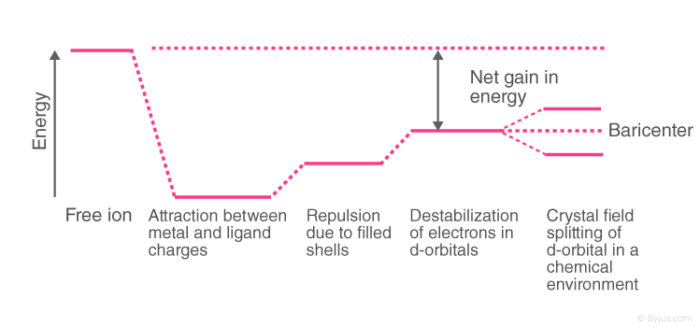
Crystal Field Splitting
Crystal field theory was proposed which described the metal-ligand bond as an ionic bond arising purely from the electrostatic interactions between the metal ions and ligands. Crystal field theory considers anions as point charges and neutral molecules as dipoles.
When transition metals are not bonded to any ligand, their d orbitals are degenerate that is they have the same energy. When they start bonding with other ligands, due to different symmetries of the d orbitals and the inductive effect of the ligands on the electrons, the d orbitals split apart and become non-degenerate.
High Spin and Low SpinThe complexion with the greater number of unpaired electrons is known as the high spin complex, the low spin complex contains the lesser number of unpaired electrons. High spin complexes are expected with weak field ligands whereas the crystal field splitting energy is small Δ. The opposite applies to the low spin complexes in which strong field ligands cause maximum pairing of electrons in the set of three t2 atomic orbitals due to large Δo.
- High spin – Maximum number of unpaired electrons.
- Low spin – Minimum number of unpaired electrons.
Example: [Co(CN)6]3- & [CoF6]3-
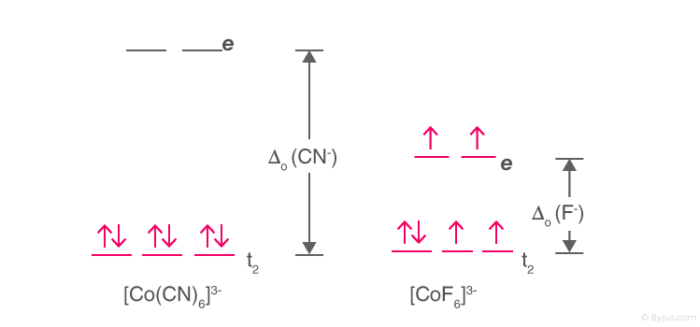
High Spin and Low Spin Complex
- [Co(CN)6]3- – Low spin complex
- [CoF6]3- – High spin complex
Splitting of d-Orbital Energies in an Octahedral Fields:
In a free metal (or isolated) metal cation all the five d-orbitals are degenerate (same energy). When the ligands move towards the metal cation, two electrostatic forces operate. One is the attraction between the metal cation and the ligands and the second is the electrostatic repulsion between d -electrons of the metal cation and the lone pairs of electrons on the ligands. Greater the force of attraction between the metal cation and the ligands, ligands will be more closer to the metal ion, and hence more will be the repulsion between the metal d electrons and the lone pair of electrons. This repulsion causes to increase in energy of metal d electrons. In a spherical field all the ligands are at equal distance from each of the d orbitals. The energy of each d orbital will raise by the same amount and all the five d-orbitals will still remain degenerate. In an octahedral complex, however, all the five d orbitals do not affected to same extent. Since the two orbitals (dx2–y2 and dz2) point directly towards the ligands and three orbitals (dxy, dyz, dzx) point in between the path of approaching ligands.
Therefore, the dx2 – y2 and dz2 orbitals will be more strongly repelled t han the dxy, dyz, dzx orbitals. Therefore, the energy of dx2 – y2 and dz2 will be raised and that of dxy, dyz and dzx orbitals which lie far away from the ligands will be decreased relative to the hypothetical energy state.
The set of dx2 – y2 and dz2 orbitals is referred to as eg set which is doubly degenerate and the set of dxy, dyz and dzx orbital is referred to as t2g set which is triply degenerate.
The separation of five d orbitals of metal cation into two sets of different energies is called crystal field splitting. The energy difference between two sets of orbitals which arise due to an octahedral field is called ∆o or 10 Dq, where o in ∆o stands for octahedral.
The total energy decrease of t2g set is equal to the total energy increase of eg orbitals. The eg orbitals are destabilised b y +0.6 ∆o or +6 Dq with respect to bary’s centre whereas t2g orbitals are stabilised by -0.4 ∆o or –4 Dq with respect to the bary,s centre.
Crystal Field Stabilization Energy
The energy which is released in a formation of a complex is called the crystal field stabilization energy of that complex.
For example, for a d1 system, the ground state corresponds to the configuration t2g1 Wit h respect to the barycentre, there is stabilization energy of –0.4∆o .This indicates that in a complex ion of d1 configuration 0.4∆o energy is released. This released energy is called the crystal field stabilization energy (CFSE) of d1 complex.
Similarly, for or a d2 ion, the ground state configuration is t2g2 and the CFSE is –0.8∆o and for complex having d3 configuration (t2g3) has a CFSE = –1.2∆o.
This is calculated as follows:
CFSE = (no. of electrons in t2g) x (–0.4∆o) + (no. of electrons in eg) x (+0.6∆o)
CFSE = nt2g x (–0.4∆o) + neg x (0.6∆o)
For d1, electronic configuration is t2g1 eg0: nt2g = 1, neg = 0
CFSE = 1 × (–0.4∆o) + 0 × (+0.6 ∆o)
CFSE = –0.4∆o = 4 Dq
For d2 configuration electronic configuration is t2g2 eg0, nt2g = 2, neg = 0
CFSE = 2× (–0.4∆o) + 0 × (0.6 ∆o)
CFSE = –0.8∆o = 8Dq
For d3 configuration electronic configuration is t2g3 eg0, nt2g = 3, neg = 0
CFSE = (3×–0.4∆o) + 0 = –1.2∆o
|
50 videos|92 docs|41 tests
|
FAQs on Bonding in Coordination Complexes: Crystal Field Theory - Inorganic Chemistry
| 1. What is coordination chemistry? |  |
| 2. What is crystal field theory? |  |
| 3. How does crystal field theory explain color in coordination complexes? |  |
| 4. What is the role of ligands in coordination complexes? |  |
| 5. How does crystal field theory explain the magnetic properties of coordination complexes? |  |

















