Buddy System | Operating System - Computer Science Engineering (CSE) PDF Download
Buddy System – Memory allocation technique
Static partition schemes suffer from the limitation of having the fixed number of active processes and the usage of space may also not be optimal. The buddy system is a memory allocation and management algorithm that manages memory in power of two increments. Assume the memory size is 2U, suppose a size of S is required.
- If 2U-1<S<=2U: Allocate the whole block
- Else: Recursively divide the block equally and test the condition at each time, when it satisfies, allocate the block and get out the loop.
System also keep the record of all the unallocated blocks each and can merge these different size blocks to make one big chunk.
Advantage
- Easy to implement a buddy system
- Allocates block of correct size
- It is easy to merge adjacent holes
- Fast to allocate memory and de-allocating memory
Disadvantage
- It requires all allocation unit to be powers of two
- It leads to internal fragmentation
Example:
Consider a system having buddy system with physical address space 128 KB.Calculate the size of partition for 18 KB process.
Solution: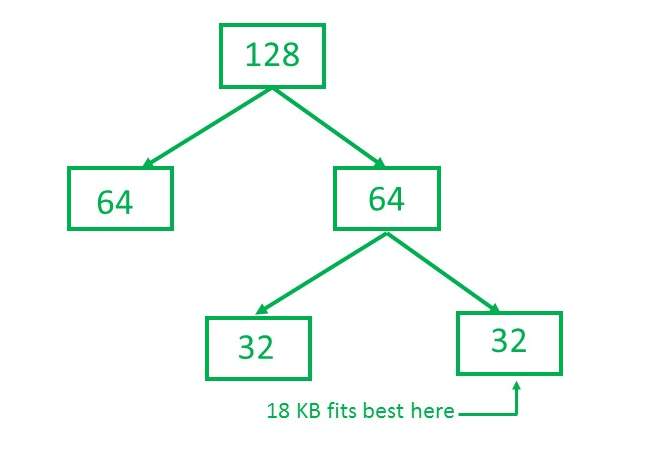
So, size of partition for 18 KB process = 32 KB. It divides by 2, till possible to get minimum block to fit 18 KB.
Buddy Memory Allocation Program
Question: Write a program to implement the buddy system of memory allocation in Operating Systems.
Explanation: The buddy system is implemented as follows- A list of free nodes, of all the different possible powers of 2, is maintained at all times (So if total memory size is 1 MB, we’d have 20 free lists to track-one for blocks of size 1 byte, 1 for 2 bytes, next for 4 bytes and so on).
When a request for allocation comes, we look for the smallest block bigger than it. If such a block is found on the free list, the allocation is done (say, the request is of 27 KB and the free list tracking 32 KB blocks has at least one element in it), else we traverse the free list upwards till we find a big enough block. Then we keep splitting it in two blocks-one for adding to the next free list (of smaller size), one to traverse down the tree till we reach the target and return the requested memory block to the user. If no such allocation is possible, we simply return null.
Example:
Let us see how the algorithm proceeds by tracking a memory block of size 128 KB. Initially, the free list is: {}, {}, {}, {}, {}, {}, {}, { (0, 127) }
- Request: 32 bytes
No such block found, so we traverse up and split the 0-127 block into 0-63, 64-127; we add 64-127 to list tracking 64 byte blocks and pass 0-63 downwards; again it is split into 0-31 and 32-63; since we have found the required block size, we add 32-63 to list tracking 32 byte blocks and return 0-31 to user.
List is: {}, {}, {}, {}, {}, { (32, 63) }, { (64, 127) }, {} - Request: 7 bytes
No such block found-split block 32-63 into two blocks, namely 32-47 and 48-63; then split 32-47 into 32-39 and 40-47; finally, return 32-39 to user (internal fragmentation of 1 byte occurs)
List is: {}, {}, {}, { (40, 47) }, { (48, 63) }, {}, { (64, 127) }, {} - Request: 64 bytes
Straight up memory segment 64-127 will be allocated as it already exists.
List is: {}, {}, {}, { (40, 47) }, { (48, 63) }, {}, {}, {} - Request: 56 bytes
Result: Not allocated
The result will be as follows:
 Buddy Allocation-128 shows the starting address of next possible block (if main memory size ever increases)
Buddy Allocation-128 shows the starting address of next possible block (if main memory size ever increases)
Question: Write a program to implement the buddy system of memory allocation and deallocation in Operating Systems.
Explanation: As we already know from Set 1, the allocation is done via the usage of free lists. Now, for deallocation, we will maintain an extra data structure-a Map (unordered_set in C++, HashMap in Java) with the starting address of segment as key and size of the segment as value and update it whenever an allocation request comes. Now, when deallocation request comes, we will first check the map to see if it is a valid request. If so, we will then add the block to the free list tracking blocks of its sizes. Then, we will search the free list to see if it’s buddy is free-if so, we will merge the blocks and place them on the free list above them (which tracks blocks of double the size), else we will not coalesce and simply return after that.
How to know which block is a given block’s buddy?
Let us define two terms-buddyNumber and buddyAddress. The buddyNumber of a block is calculated by the formula:
(base_address-starting_address_of_main_memory)/block_size
We note that this is always an integer, as both numerator and denominator are powers of 2. Now, a block will be another block’s buddy if both of them were formed by the splitting of the same bigger block. For example, if 4 consecutive allocation requests of 16 bytes come, we will end up with blocks 0-15, 16-31, 32-47, 48-63 where blocks 0-15 and 16-31 are buddies (as they were formed by splitting block 0-32) but 0-15 and 32-47 aren’t. The buddyAddress of a block is the starting index of its buddy block, given by the formula:
block_starting_address+block_size (if buddyNumber is even)
block_starting_address-block_size (if buddyNumber is odd)
Thus, all we have to do is find this buddyAddress in the free list (by comparing with all the starting addresses in that particular list), and if present, coalescing can be done.
Examples:
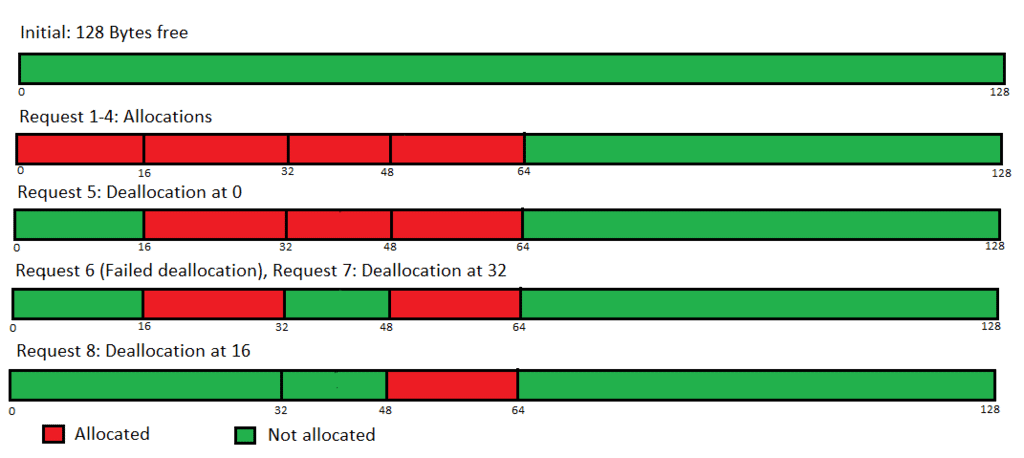
Let us see how the algorithm proceeds by tracking a memory block of size 128 KB. Initially, the free list is: {}, {}, {}, {}, {}, {}, {}, { (0, 127) }
- Allocation Request: 16 bytes
No such block found, so we traverse up and split the 0-127 block into 0-63, 64-127; we add 64-127 to list tracking 64 byte blocks and pass 0-63 downwards; again it is split into 0-31 and 32-63; we add 32-63 to list tracking 32 byte blocks, passing 0-31 downwards; one more spli is done and 0-15 is returned to user while 16-31 is added to free list tracking 16 byte blocks.
List is: {}, {}, {}, {}, { (16, 31) }, { (32, 63) }, { (64, 127) }, {} - Allocation Request: 16 bytes
Straight up memory segment 16-31 will be allocated as it already exists.
List is: {}, {}, {}, {}, {}, { (32, 63) }, { (64, 127) }, {} - Allocation Request: 16 bytes
No such block found, so we will traverse up to block 32-63 and split it to blocks 32-47 and 48-63; we will add 48-63 to list tracking 16 byte blocks and return 32-47 to user.
List is: {}, {}, {}, {}, { (48, 63) }, {}, { (64, 127) }, {} - Allocation Request: 16 bytes
Straight up memory segment 48-63 will be allocated as it already exists.
List is: {}, {}, {}, {}, {}, {}, { (64, 127) }, {} - Deallocation Request: StartIndex = 0
Deallocation will be done but no coalesscing is possible as it’s buddyNumber is 0 and buddyAddress is 16 (via the formula), none of which is in the free list.
List is: {}, {}, {}, {}, { (0, 15) }, {}, { (64, 127) }, {} - Deallocation Request: StartIndex = 9
Result: Invalid request, as this segmeent was never allocated.
List is: {}, {}, {}, {}, { (0, 15) }, {}, { (64, 127) }, {} - Deallocation Request: StartIndex = 32
Deallocation will be done but no coalesscing is possible as the buddyNumber of the blocks are 0 and 2 buddyAddress of the blocks are 16 and 48, repectively, none of which is in the free list.
List is: {}, {}, {}, {}, { (0, 15), (32-47) }, {}, { (64, 127) }, {} - Deallocation Request: StartIndex = 16
Deallocation will be done and coealsecing of the blocks 0-15 and 16-31 will also be done as the buddyAddress of block 16-31 is 0, which is present in the free list tracking 16 byte blocks.
List is: {}, {}, {}, {}, { (32-47) }, { (0, 31) }, { (64, 127) }, {} Buddy algorithm-allocation and deallocation
Buddy algorithm-allocation and deallocation
|
10 videos|99 docs|33 tests
|
FAQs on Buddy System - Operating System - Computer Science Engineering (CSE)
| 1. What is the buddy system memory allocation technique? |  |
| 2. How does the buddy system memory allocation technique work? |  |
| 3. What are the advantages of using the buddy system memory allocation technique? |  |
| 4. What are the limitations of the buddy system memory allocation technique? |  |
| 5. How does the buddy system memory allocation technique compare to other memory allocation techniques? |  |