Tables CAT Previous Year Questions with Answer PDF
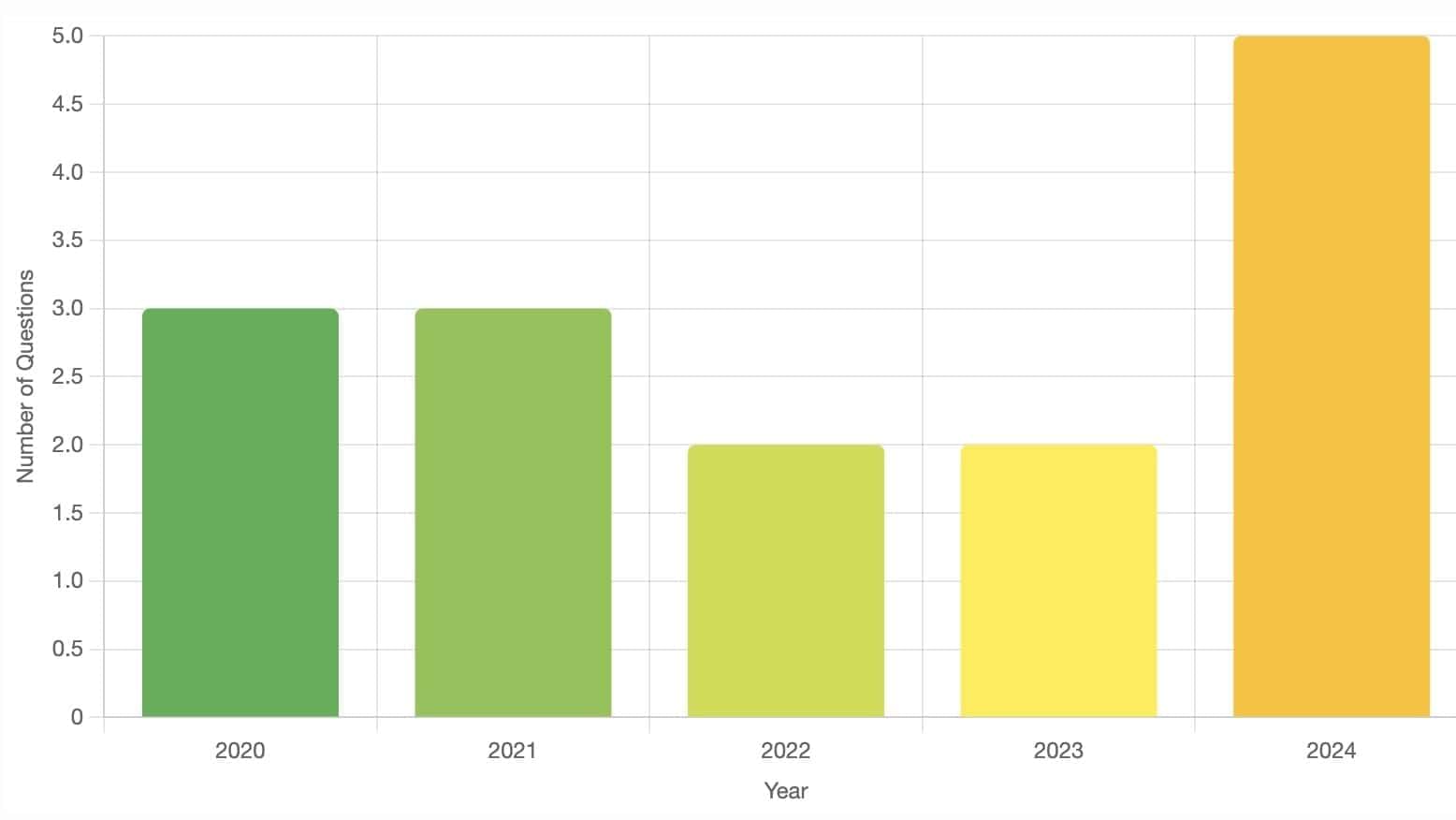
From 2020 to 2024, CAT featured one set of table-related questions each year, with 2 to 5 questions per set. These questions focused on data interpretation and logical reasoning using tabular data, ranging from moderate to challenging, and required skills in analysing structured information, identifying patterns, and performing multi-step deductions.
2024
Passage - 1
Direction: Answer the following questions based on the information given below.
Six web surfers M, N, O, P, X, and Y each had 30 stars which they distributed among four bloggers A, B, C, and D. The number of stars received by A and B from the six web surfers is shown in the figure below.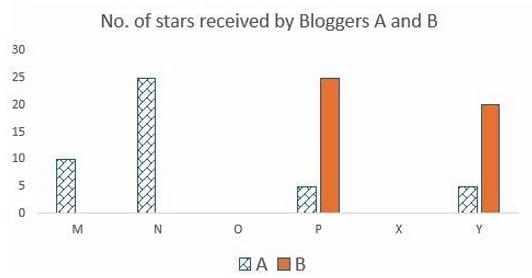 The following additional facts are known regarding the number of stars received by the
The following additional facts are known regarding the number of stars received by the
bloggers from the surfers.
1. The numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0).
2. The total numbers of stars received by the bloggers were the same.
3. Each blogger received a different number of stars from M.
4. Two surfers gave all their stars to a single blogger.
5. D received more stars than C from Y
Q1: What was the total number of stars received by D?
Ans: 45
Sol: With the given data we can make the following table:
From statement 2 we can say that each blogger received 180/4 = 45 stars.
Now from statements 1 and 3, we can say that C and D will get 5 and 15 stars from M in any order.
It is given that two surfers will give all their stars to a single blogger so O and X will give all their stars to C and D. From statement 5 we can say that D will get 5 stars from Y and C will get 0.
For C and D the total must be 45 stars each, here D cannot get 15 stars from M, because then his total will be more than 45 as he gets 30 points from either O or X. So, D will get 5 stars from M and C will get 15 stars from M. Now C gets the total of 45 stars in which M gives 15 and one of O or X gives 30. For D, M will give 5, and one of O or X will give 30 and N will give 5 stars. We will get the final table as given below.
Q2: What was the number of stars received by D from Y?
(a) 10
(b) 0
(c) 5
(d) Cannot be determined
Ans: c
Sol: With the given data we can make the following table:
From statement 2 we can say that each blogger received 180/4 = 45 stars.
Now from statements 1 and 3, we can say that C and D will get 5 and 15 stars from M in any order.
It is given that two surfers will give all their stars to a single blogger so O and X will give all their stars to C and D. From statement 5 we can say that D will get 5 stars from Y and C will get 0.
For C and D the total must be 45 stars each, here D cannot get 15 stars from M, because then his total will be more than 45 as he gets 30 points from either O or X. So, D will get 5 stars from M and C will get 15 stars from M. Now C gets the total of 45 stars in which M gives 15 and one of O or X gives 30. For D, M will give 5, and one of O or X will give 30 and N will give 5 stars. We will get the final table as given below.
Q3: How many surfers distributed their stars among exactly 2 bloggers?
Ans: 2
Sol: With the given data we can make the following table:
From statement 2 we can say that each blogger received 180/4 = 45 stars.
Now from statements 1 and 3, we can say that C and D will get 5 and 15 stars from M in any order.
It is given that two surfers will give all their stars to a single blogger so O and X will give all their stars to C and D. From statement 5 we can say that D will get 5 stars from Y and C will get 0.
For C and D the total must be 45 stars each, here D cannot get 15 stars from M, because then his total will be more than 45 as he gets 30 points from either O or X. So, D will get 5 stars from M and C will get 15 stars from M. Now C gets the total of 45 stars in which M gives 15 and one of O or X gives 30. For D, M will give 5, and one of O or X will give 30 and N will give 5 stars. We will get the final table as given below.
Only N and P distributed their stars among exactly 2 bloggers
Q4: Which of the following can be determined with certainty?
I. The number of stars received by C from M
II. The number of stars received by D from O
A: Only I
B: Neither I nor II
C: Both I and II
D: Only II
Ans: A
Sol: With the given data we can make the following table:
From statement 2 we can say that each blogger received 180/4 = 45 stars.
Now from statements 1 and 3, we can say that C and D will get 5 and 15 stars from M in any order.
It is given that two surfers will give all their stars to a single blogger so O and X will give all their stars to C and D. From statement 5 we can say that D will get 5 stars from Y and C will get 0.
For C and D the total must be 45 stars each, here D cannot get 15 stars from M, because then his total will be more than 45 as he gets 30 points from either O or X. So, D will get 5 stars from M and C will get 15 stars from M. Now C gets the total of 45 stars in which M gives 15 and one of O or X gives 30. For D, M will give 5, and one of O or X will give 30 and N will give 5 stars. We will get the final table as given below.
Answer: option A.
Passage - 2
Answer the following questions based on the information given below.
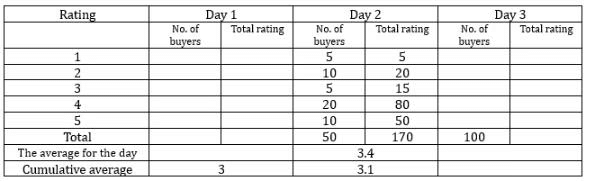
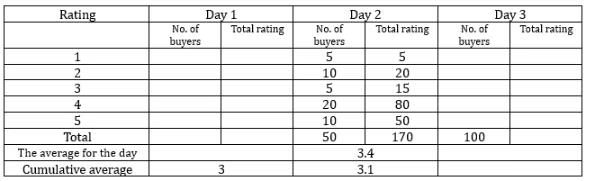
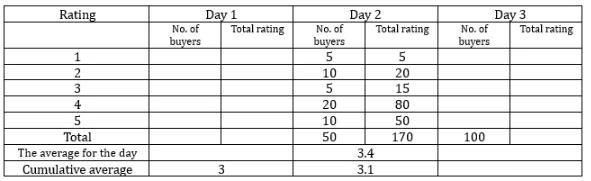
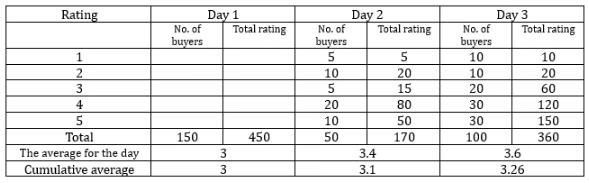
An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day. The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below.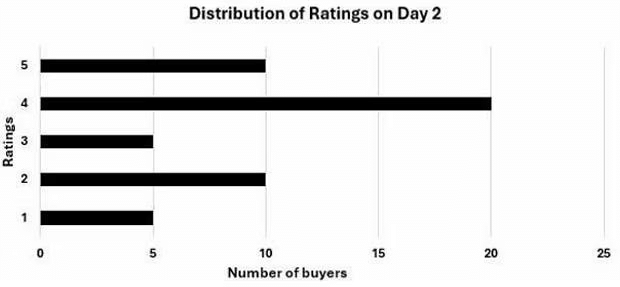
The following information is known about ratings on Day 3.
1. 100 buyers gave product ratings on Day 3.
2. The modes of the product ratings were 4 and 5.
3. The numbers of buyers giving each product rating are non-zero multiples of 10.
4. The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3.
Q1: How many buyers gave ratings on Day 1?
Ans: 150
Sol: The given data in the bar graph is for day 2 and the given data in the statements are for day 3. Tabulating the given data we get.
The average and cumulative average for day 1 will be the same i.e. 3. Let the total number of buyers on day 1 be n. According to the statements.(3n+170)/(50+n) = 3.1
3n + 170 = 155 + 3.1n
15 = 0.1n
n = 150
so the number of buyers on day 1 will be equal to 150.
It is given that the mode ratings on day 3 are 4, and 5 hence the number of buyers who gave ratings of 4 and 5 will be equal. It is given that the total number of buyers is 100 and for every rating the number of buyers is a nonzero integral multiple of 10. So the number of buyers who gave the rating for 4, and 5 must be 30 each. Because the number of buyers who gave a rating of 4 and 5 must be more than the other ratings and must be an integral multiple of 10. The number of buyers who gave ratings of 1, and 2 are equal and it will be 10 each and for the rating 3, it is double i.e. 20. So with this information, we can make the following table. So, the cumulative average for day 3 will be equal to
C3 = 450+170+360/150+50+100 = 980/300 = 3.266
As we can see from the above table there are a total of 150 buyers on day 1.
Q2: What is the daily average rating of Day 3?
(a) 3.0
(b) 3.5
(c) 3.2
(d) 3.6
Ans: d
Sol: The given data in the bar graph is for day 2 and the given data in the statements are for day 3. Tabulating the given data we get.
The average and cumulative average for day 1 will be the same i.e. 3. Let the total number of buyers on day 1 be n. According to the statements.(3n+170)/(50+n) = 3.1
3n + 170 = 155 + 3.1n
15 = 0.1n
n = 150
so the number of buyers on day 1 will be equal to 150.
It is given that the mode ratings on day 3 are 4, and 5 hence the number of buyers who gave ratings of 4 and 5 will be equal. It is given that the total number of buyers is 100 and for every rating the number of buyers is a nonzero integral multiple of 10. So the number of buyers who gave the rating for 4, and 5 must be 30 each. Because the number of buyers who gave a rating of 4 and 5 must be more than the other ratings and must be an integral multiple of 10. The number of buyers who gave ratings of 1, and 2 are equal and it will be 10 each and for the rating 3, it is double i.e. 20. So with this information, we can make the following table. So, the cumulative average for day 3 will be equal to
C3 = 450+170+360/150+50+100 = 980/300 = 3.266
As we can see from the above table the average rating for Day 3 is 3.6.
Q3: What is the median of all ratings given on Day 3?
Ans: 4
Sol: The given data in the bar graph is for day 2 and the given data in the statements are for day 3. Tabulating the given data we get.
The average and cumulative average for day 1 will be the same i.e. 3. Let the total number of buyers on day 1 be n. According to the statements.(3n+170)/(50+n) = 3.1
3n + 170 = 155 + 3.1n
15 = 0.1n
n = 150
so the number of buyers on day 1 will be equal to 150.
It is given that the mode ratings on day 3 are 4, and 5 hence the number of buyers who gave ratings of 4 and 5 will be equal. It is given that the total number of buyers is 100 and for every rating the number of buyers is a nonzero integral multiple of 10. So the number of buyers who gave the rating for 4, and 5 must be 30 each. Because the number of buyers who gave a rating of 4 and 5 must be more than the other ratings and must be an integral multiple of 10. The number of buyers who gave ratings of 1, and 2 are equal and it will be 10 each and for the rating 3, it is double i.e. 20. So with this information, we can make the following table. So, the cumulative average for day 3 will be equal to
C3 = 450+170+360/150+50+100 = 980/300 = 3.266
On day 3 there are 10 ratings of 1, 10 ratings of 2, 20 ratings of 3, 30 ratings of 4, and 30 ratings of 5. So the median rating will be 4.
Q4: Which of the following is true about the cumulative average ratings of Day 2 and Day 3?
(a) The cumulative average of Day 3 increased by a percentage between 5% and 8% from Day 2.
(b) The cumulative average of Day 3 increased by more than 8% from Day 2.
(c) The cumulative average of Day 3 decreased from Day 2.
(d) The cumulative average of Day 3 increased by less than 5% from Day 2.
Ans: (a)
Sol: The given data in the bar graph is for day 2 and the given data in the statements are for day 3. Tabulating the given data we get.
The average and cumulative average for day 1 will be the same i.e. 3. Let the total number of buyers on day 1 be n. According to the statements.(3n+170)/(50+n) = 3.1
3n + 170 = 155 + 3.1n
15 = 0.1n
n = 150
so the number of buyers on day 1 will be equal to 150.
It is given that the mode ratings on day 3 are 4, and 5 hence the number of buyers who gave ratings of 4 and 5 will be equal. It is given that the total number of buyers is 100 and for every rating the number of buyers is a nonzero integral multiple of 10. So the number of buyers who gave the rating for 4, and 5 must be 30 each. Because the number of buyers who gave a rating of 4 and 5 must be more than the other ratings and must be an integral multiple of 10. The number of buyers who gave ratings of 1, and 2 are equal and it will be 10 each and for the rating 3, it is double i.e. 20. So with this information, we can make the following table. So, the cumulative average for day 3 will be equal to
C3 = 450+170+360/150+50+100 = 980/300 = 3.266
The cumulative rating on day 3 is 3.26 and on day 2 is 3.1, so there is an increase, and the increase % = 3.26-3.1/3.1 *100 = 5.16%. So, the correct option is 1.
Passage - 3
Answer the following questions based on the information given below.
Over the top (OTT) subscribers of a platform are segregated into three categories: i) Kid, ii) Elder, and iii) Others. Some of the subscribers used one app and the others used multiple apps to access the platform. The figure below shows the percentage of the total number of subscribers in 2023 and 2024 who belong to the ‘Kid’ and ‘Elder’ categories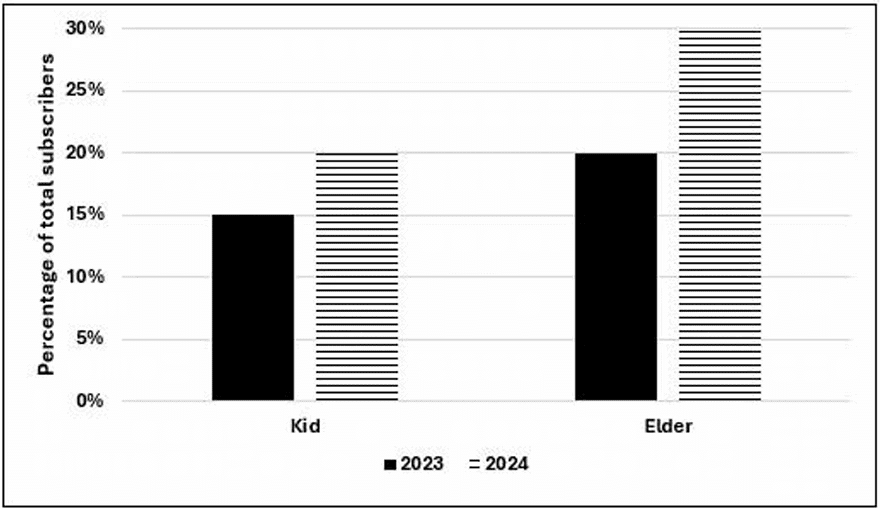
The following additional facts are known about the numbers of subscribers.
1. The total number of subscribers increased by 10% from 2023 to 2024.
2. In 2024, 1/2 of the subscribers from the ‘Kid’ category and 2/3 of the subscribers from the ‘Elder’ category subscribers use one app.
3. In 2023, the number of subscribers from the ‘Kid’ category who used multiple apps was the same as the number of subscribers from the ‘Elder’ category who used one app.
4. 10,000 subscribers from the ‘Kid’ category used one app and 15,000 subscribers from the ‘Elder’ category used multiple apps in 2023.
Q1: How many subscribers belonged to the ‘Others’ category in 2024?
(a) 65000
(b) Cannot be determined
(c) 55000
(d) 45000
Ans: c
Sol: We can tabulate the given data as shown below:We know that there were 15% kids and 20% elders in the total subscribers of the year 2023. So, according to the problem:15% of y = 10000+x--------1
20% of y = 15000+x---------2
From 1 and 2 we get,
x = 5000
So, the total subscribers in 2023 are equal to = y = 20000*5 = 100000
So, the total subscribers in 2024 are equal to = 1.1y = 110000
With this information, we can fill the table remaining table:
Q2: What percentage of subscribers in the ‘Kid’ category used multiple apps in 2023?
(a) 33.33%
(b) 5%
(c) 25.5%
(d) 50%
Ans: a
Sol: We can tabulate the given data as shown below:We know that there were 15% kids and 20% elders in the total subscribers of the year 2023. So, according to the problem:15% of y = 10000+x--------1
20% of y = 15000+x---------2
From 1 and 2 we get,
x = 5000
So, the total subscribers in 2023 are equal to = y = 20000*5 = 100000
So, the total subscribers in 2024 are equal to = 1.1y = 110000
With this information, we can fill the table remaining table:
Required percentage = 5000/15000 *100 = 33.33%
Q3: What was the percentage increase in the number of subscribers in the ‘Elder’ category from 2023 to 2024?
(a) 40%
(b) 50%
(c) 60%
(d) 65%
Ans: d
Sol: We can tabulate the given data as shown below:We know that there were 15% kids and 20% elders in the total subscribers of the year 2023. So, according to the problem:15% of y = 10000+x--------1
20% of y = 15000+x---------2
From 1 and 2 we get,
x = 5000
So, the total subscribers in 2023 are equal to = y = 20000*5 = 100000
So, the total subscribers in 2024 are equal to = 1.1y = 110000
With this information, we can fill the table remaining table:
The required percentage = 13000/20000 * 100 = 65%
Q4: What could be the minimum percentage of subscribers who used multiple apps in 2024?
(a) 20%
(b) 22%
(c) 16.5%
(d) 10%
Ans: a
Sol: We can tabulate the given data as shown below:We know that there were 15% kids and 20% elders in the total subscribers of the year 2023. So, according to the problem:15% of y = 10000+x--------1
20% of y = 15000+x---------2
From 1 and 2 we get,
x = 5000
So, the total subscribers in 2023 are equal to = y = 20000*5 = 100000
So, the total subscribers in 2024 are equal to = 1.1y = 110000
With this information, we can fill the table remaining table:
It is given that 10% of kids and 10% of adults use multiple apps in 2024, so the minimum percentage will be 20%.
Passage - 4
Answer the following questions based on the information given below.
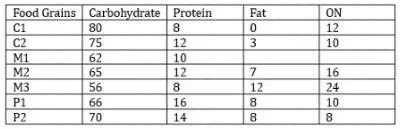
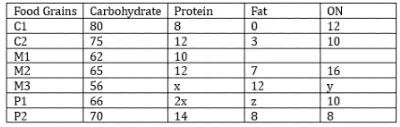
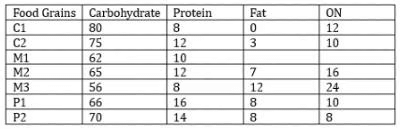
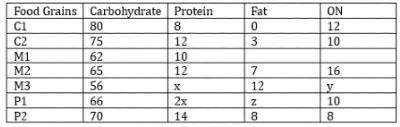
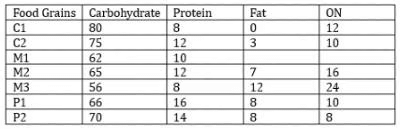
The table given below shows the amount, in grams, of carbohydrate, protein, fat and all other nutrients, per 100 grams of nutrients in seven foodgrains. The first column shows the foodgrain category and the second column its odename. The table has some missing values.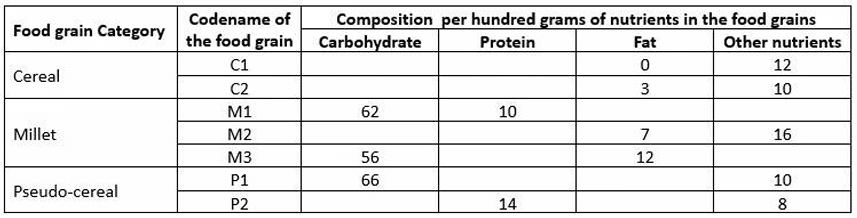
The following additional facts are known.
1. Both the pseudo-cereals had higher amounts of carbohydrate as well as higher amounts of protein than any millet.
2. Both the cereals had higher amounts of carbohydrate than any pseudo-cereal.
3. All the missing values of carbohydrate amounts (in grams) for all the foodgrains are non-zero multiples of 5.
4. All the missing values of protein, fat and other nutrients amounts (in grams) for all the foodgrains are non-zero multiples of 4.
5. P1 contained double the amount of protein that M3 contains.
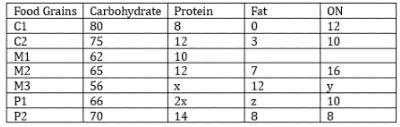
Q1: How many foodgrains had a higher amount of carbohydrate per 100 grams of nutrients than M1?
Ans: 5
Sol: From statements 1, 2, and 3 we can say that the C1 and C2 must contain at least 70 grams of Carbohydrates and P2 will contain at least 65 grams of Carbohydrates.
From statement 4 we can say that all the sub-compositions must be non-zero multiples of 4. With this information, we can try to find the compositions for the Cereals.
For C1:
100 – 12 = 88 = 5c+4p
Now the only possible value of 5c with 5c being at least 70, is 80 and we will get 4p as 8
For C2:
100 – 13 = 87 = 5c + 4p
Now the only possible value of 5c with 5c being at least 70, is 75 and we will get 4p as 12
For P2:
Now the carbohydrates of P2 can only take values of either 65 or 70, it cannot be 65 because 100 – 65 – 22 = 13, which is not a multiple of 4. So the only possible value is 70 and 100 – 70 – 22 = 8, which is a multiple of 4. So this is the correct case.For M2:
100 – 7 – 16 = 77 = 5c + 4p, here 4p must be less than 14 and 5c must be less than 70. The only possible values for 5c and 4c are 65 and 12 respectively.
We can plug these values into a table:
Now x + y = 32, and 2x+ z = 24, here 2x must be greater than 12, and x, y, and z must be non-zero multiples of 4. The only possible values of x, y, and z are 8, 24, and 8 respectively.
Q2: How many grams of protein were there in 100 grams of nutrients in M2?
Ans: 12
Sol: From statements 1, 2, and 3 we can say that the C1 and C2 must contain at least 70 grams of Carbohydrates and P2 will contain at least 65 grams of Carbohydrates.
From statement 4 we can say that all the sub-compositions must be non-zero multiples of 4. With this information, we can try to find the compositions for the Cereals.
For C1:
100 – 12 = 88 = 5c+4p
Now the only possible value of 5c with 5c being at least 70, is 80 and we will get 4p as 8
For C2:
100 – 13 = 87 = 5c + 4p
Now the only possible value of 5c with 5c being at least 70, is 75 and we will get 4p as 12
For P2:
Now the carbohydrates of P2 can only take values of either 65 or 70, it cannot be 65 because 100 – 65 – 22 = 13, which is not a multiple of 4. So the only possible value is 70 and 100 – 70 – 22 = 8, which is a multiple of 4. So this is the correct case.
For M2:
100 – 7 – 16 = 77 = 5c + 4p, here 4p must be less than 14 and 5c must be less than 70. The only possible values for 5c and 4c are 65 and 12 respectively.
We can plug these values into a table:
Now x + y = 32, and 2x+ z = 24, here 2x must be greater than 12, and x, y, and z must be non-zero multiples of 4. The only possible values of x, y, and z are 8, 24, and 8 respectively.
Q3: How many grams of other nutrients were there in 100 grams of nutrients in M3?
Ans: 24
Sol: From statements 1, 2, and 3 we can say that the C1 and C2 must contain at least 70 grams of Carbohydrates and P2 will contain at least 65 grams of Carbohydrates.
From statement 4 we can say that all the sub-compositions must be non-zero multiples of 4. With this information, we can try to find the compositions for the Cereals.
For C1:
100 – 12 = 88 = 5c+4p
Now the only possible value of 5c with 5c being at least 70, is 80 and we will get 4p as 8
For C2:
100 – 13 = 87 = 5c + 4p
Now the only possible value of 5c with 5c being at least 70, is 75 and we will get 4p as 12
For P2:
Now the carbohydrates of P2 can only take values of either 65 or 70, it cannot be 65 because 100 – 65 – 22 = 13, which is not a multiple of 4. So the only possible value is 70 and 100 – 70 – 22 = 8, which is a multiple of 4. So this is the correct case.For M2:
100 – 7 – 16 = 77 = 5c + 4p, here 4p must be less than 14 and 5c must be less than 70. The only possible values for 5c and 4c are 65 and 12 respectively.
We can plug these values into a table:
Now x + y = 32, and 2x+ z = 24, here 2x must be greater than 12, and x, y, and z must be non-zero multiples of 4. The only possible values of x, y, and z are 8, 24, and 8 respectively.
Q4: What is the median of the number of grams of protein in 100 grams of nutrients among these food grains?
Ans: 12
Sol: From statements 1, 2, and 3 we can say that the C1 and C2 must contain at least 70 grams of Carbohydrates and P2 will contain at least 65 grams of Carbohydrates.
From statement 4 we can say that all the sub-compositions must be non-zero multiples of 4. With this information, we can try to find the compositions for the Cereals.
For C1:
100 – 12 = 88 = 5c+4p
Now the only possible value of 5c with 5c being at least 70, is 80 and we will get 4p as 8
For C2:
100 – 13 = 87 = 5c + 4p
Now the only possible value of 5c with 5c being at least 70, is 75 and we will get 4p as 12
For P2:
Now the carbohydrates of P2 can only take values of either 65 or 70, it cannot be 65 because 100 – 65 – 22 = 13, which is not a multiple of 4. So the only possible value is 70 and 100 – 70 – 22 = 8, which is a multiple of 4. So this is the correct case.For M2:
100 – 7 – 16 = 77 = 5c + 4p, here 4p must be less than 14 and 5c must be less than 70. The only possible values for 5c and 4c are 65 and 12 respectively.
We can plug these values into a table:
Now x + y = 32, and 2x+ z = 24, here 2x must be greater than 12, and x, y, and z must be non-zero multiples of 4. The only possible values of x, y, and z are 8, 24, and 8 respectively.
Passage - 5
Answer the following questions based on the information given below.
Out of 10 countries -- Country 1 through Country 10 -- Country 9 has the highest gross domestic product (GDP), and Country 10 has the highest GDP per capita. GDP per capita is the GDP of a country divided by its population. The table below provides the following data about Country 1 through Country 8 for the year 2024.
- Column 1 gives the country's identity.
- Column 2 gives the country’s GDP as a fraction of the GDP of Country 9.
- Column 3 gives the country’s GDP per capita as a fraction of the GDP per capita of Country 10.
- Column 4 gives the country’s annual GDP growth rate.
- Column 5 gives the country’s annual population growth rate.
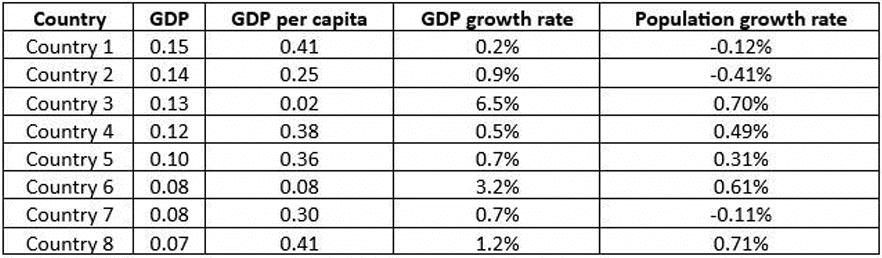
Assume that the GDP growth rates and population growth rates of the countries will remain constant for the next three years
Q1: Which one among the countries 1 through 8, has the smallest population in 2024?
(a) Country 7
(b) Country 3
(c) Country 5
(d) Country 8
Ans: d
Sol: Per Capita GDP = GDP/ population
Population = GDP/per capita GDP
For the population to be low the GDP must be low and the per capita GDP must be high. For the given four options we can observe that country 8 has the smallest population.
Q2: The ratio of Country 4’s GDP to Country 5’s GDP in 2026 will be closest to
(a) 1.195
(b) 0.963
(c) 1.032
(d) 1.314
Ans: a
Sol: Ratio = 0.12*1.005*1.005/0.1*1.007*1.007 = 1.195238099934026
Q3: Which one among the countries 1, 4, 5, and 7 will have the largest population in 2027?
(a) Country 7
(b) Country 1
(c) Country 4
(d) Country 5
Ans: b
Sol: Using the same method we used in the first question we can observe that country 1 has the largest population.
Q4: For how many countries among Country 1 through Country 8 will the GDP per capita in 2027 be lower than that in 2024?
Ans: 0
Sol: We can see that from the above table, the GDP growth rate of all the countries from 1 to 8 is more than the population growth rate. So 0 countries will have a GDP per capita in 2027 lower than 2024.
2023
Passage - 1
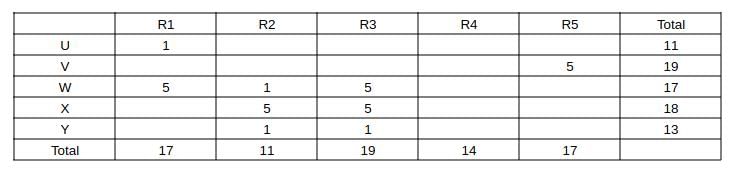
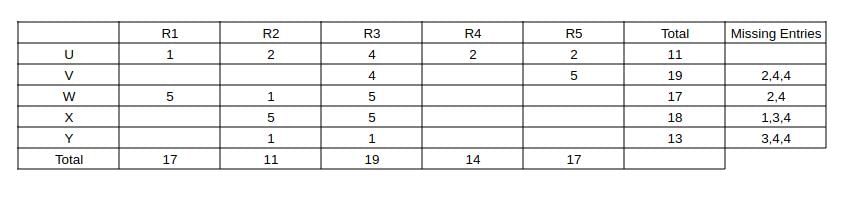
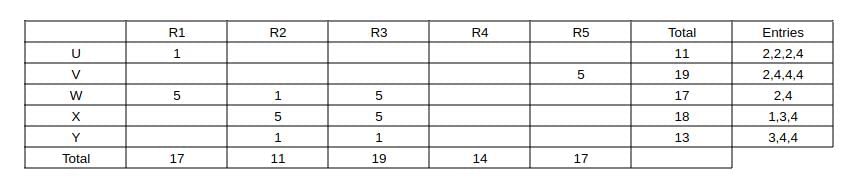
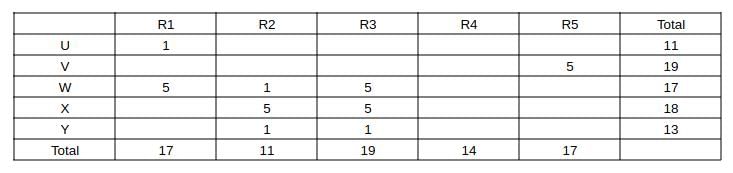
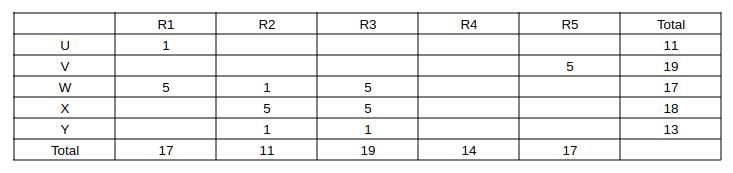
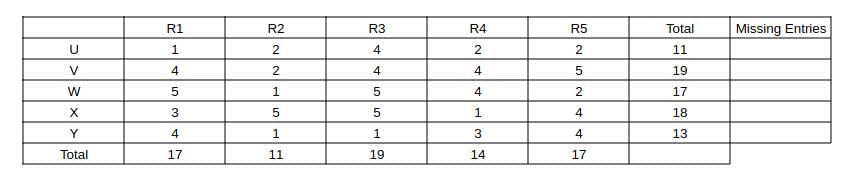
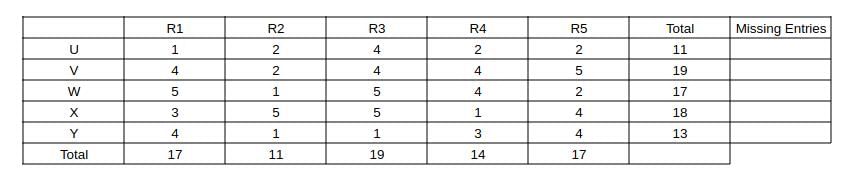
Five restaurants, coded R1, R2, R3, R4 and R5 gave integer ratings to five gig workers -
Ullas, Vasu, Waman, Xavier and Yusuf, on a scale of 1 to 5.
The means of the ratings given by R1, R2, R3, R4 and R5 were 3.4, 2.2, 3.8, 2.8 and 3.4 respectively.
The summary statistics of these ratings for the five workers is given below.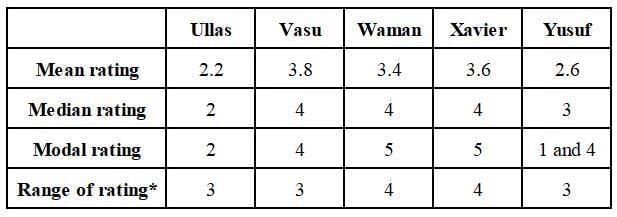
* Range of ratings is defined as the difference between the maximum and minimum ratings awarded to a worker.
The following is partial information about ratings of 1 and 5 awarded by the restaurants to the workers.
(a) R1 awarded a rating of 5 to Waman, as did R2 to Xavier, R3 to Waman and Xavier, and R5 to Vasu.
(b) R1 awarded a rating of 1 to Ullas, as did R2 to Waman and Yusuf, and R3 to Yusuf.
Q1: How many individual ratings cannot be determined from the above information?
Ans: 0
Sol: Given that the means of the ratings given by R1, R2, R3, R4 and R5 were 3.4, 2.2, 3.8, 2.8 and 3.4 respectively.
=> The sum of ratings given by R1, R2, R3 R4, R5 are 5*means = 17, 11, 19, 14, and 17 respectively.
Similarly the sum of ratings received by U, V, W, X and Y are 5*means = 11, 19, 17, 18, and 13 respectively.
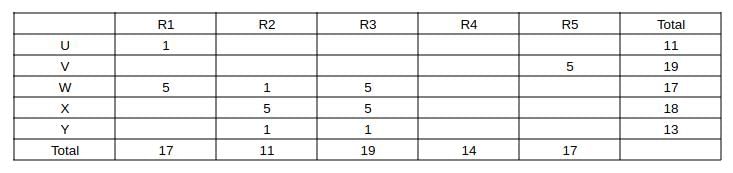
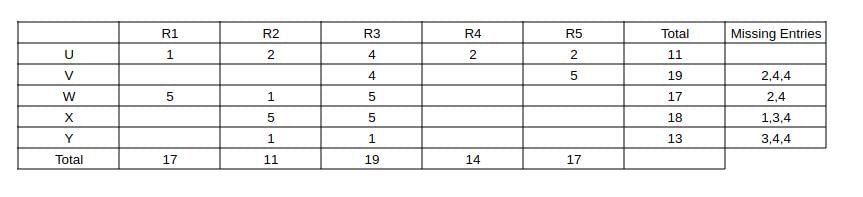
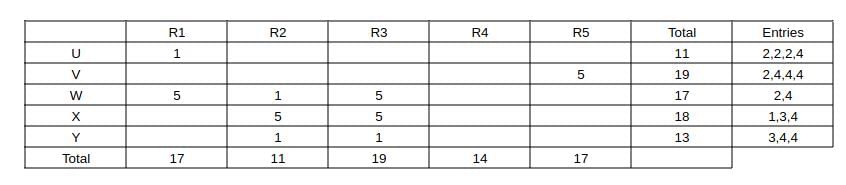
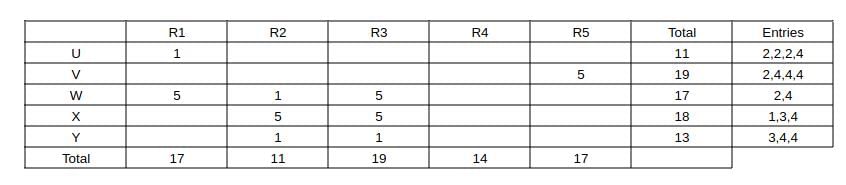
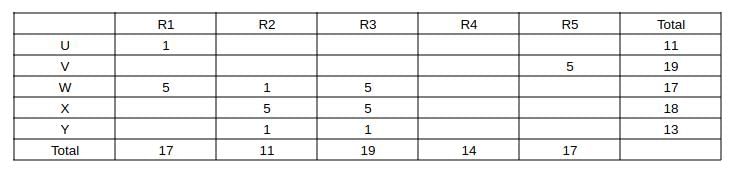
Also capturing the absolute data given in the partial information (a) and (b) and representing as a table, we get:
Now,
Consider U
Given median = 2, mode = 2 and range = 3
=> His ratings should be of the form 1, a , 2, b, 4 => 1 + 2 + 4 + a + b = 11 => a + b = 4. For mode = 2 => a = b = 2
=> U's ratings are 1, 2, 2, 2, 4.
Consider V
Given median = 4, mode = 4 and range = 3
=> His ratings should be of the form 2, a, 4, b, 5 => 2 + 4 + 5 + a + b = 19 => a + b = 8 => For mode = 4 => a = b = 4
=> V's ratings are 2, 4, 4, 4, 5.
Consider W
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => 1 + a + 4 + 5 + 5 = 17 => a = 2
=> W's ratings are 1, 2, 4, 5, 5.
Consider X
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => a + 1 + 4 + 5 + 5 = 18 => a = 3
=> X's ratings are 1, 3, 4, 5, 5
Consider Y
Given median = 3, mode = 1 & 4, Range = 3
=> His ratings are 1, 1, 3, 4, 4.
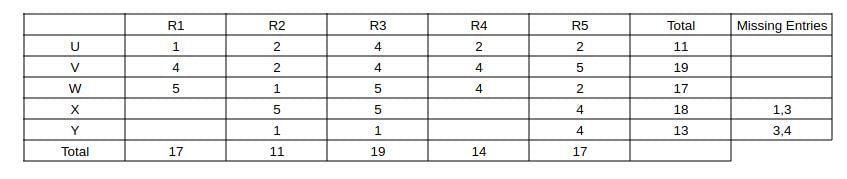
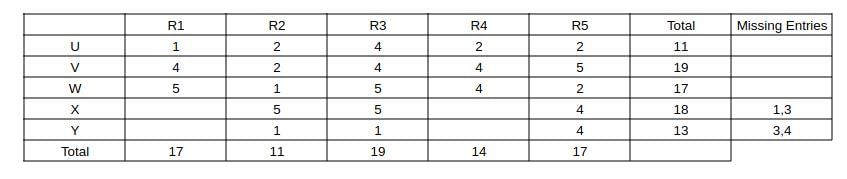
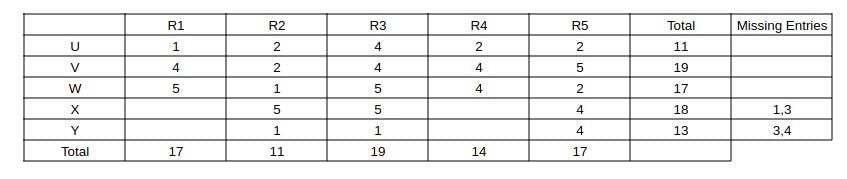
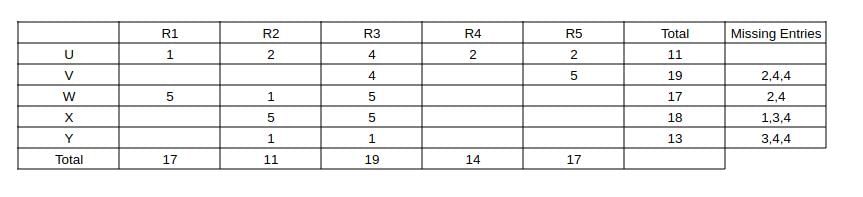
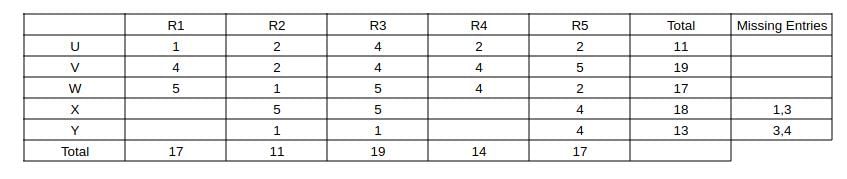
Capturing this data in the table, we get:
Now, consider column R3 => The two missing entries should add up to 19 - 1 - 5 - 5 = 8, (only possibility is 4 + 4) => We can fill the row "U" and 4 in the row "V"
Now, consider column R2 => Missing entry should be 11 - 2 - 1 - 5 - 1 = 2
Consider column R1, the missing elements should add up to 17 - 5 - 4 - 1 = 7 (3 + 4 or 4 + 3) ----(1)
Consider R5, the missing elements should add up to 10 => 2 + 4 + 4 or 4 + 3 + 3 (not possible) as (1) requires a 3.
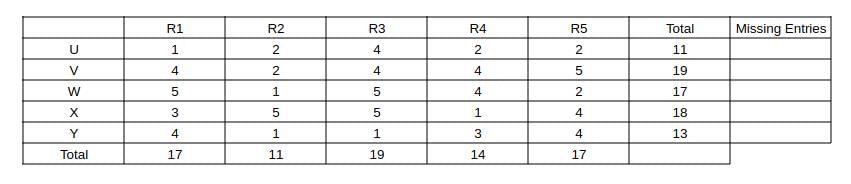
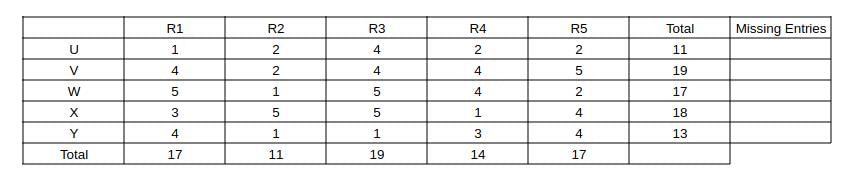
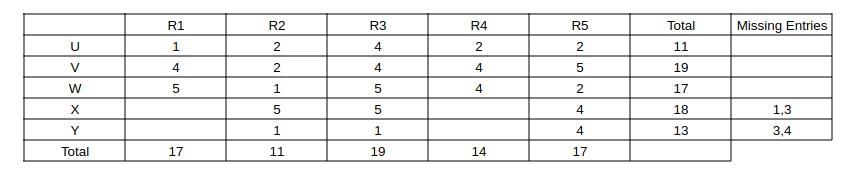
Now, we can fill column R1 as 3 + 4 and the remaining in column R4 and we can get the complete table
=> All ratings can be determined uniquely => 0.
Q2: To how many workers did R2 give a rating of 4?
Ans: 0
Sol: Given that the means of the ratings given by R1, R2, R3, R4 and R5 were 3.4, 2.2, 3.8, 2.8 and 3.4 respectively.
=> The sum of ratings given by R1, R2, R3 R4, R5 are 5*means = 17, 11, 19, 14, and 17 respectively.
Similarly the sum of ratings received by U, V, W, X and Y are 5*means = 11, 19, 17, 18, and 13 respectively.
Also capturing the absolute data given in the partial information (a) and (b) and representing as a table, we get:
Now,
Consider U
Given median = 2, mode = 2 and range = 3
=> His ratings should be of the form 1, a , 2, b, 4 => 1 + 2 + 4 + a + b = 11 => a + b = 4. For mode = 2 => a = b = 2
=> U's ratings are 1, 2, 2, 2, 4.
Consider V
Given median = 4, mode = 4 and range = 3
=> His ratings should be of the form 2, a, 4, b, 5 => 2 + 4 + 5 + a + b = 19 => a + b = 8 => For mode = 4 => a = b = 4
=> V's ratings are 2, 4, 4, 4, 5.
Consider W
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => 1 + a + 4 + 5 + 5 = 17 => a = 2
=> W's ratings are 1, 2, 4, 5, 5.
Consider X
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => a + 1 + 4 + 5 + 5 = 18 => a = 3
=> X's ratings are 1, 3, 4, 5, 5
Consider Y
Given median = 3, mode = 1 & 4, Range = 3
=> His ratings are 1, 1, 3, 4, 4.
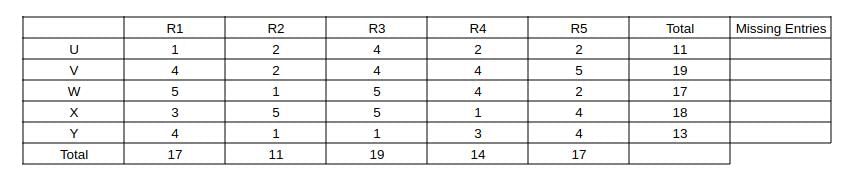
Capturing this data in the table, we get:
Now, consider column R3 => The two missing entries should add up to 19 - 1 - 5 - 5 = 8, (only possibility is 4 + 4) => We can fill the row "U" and 4 in the row "V"
Now, consider column R2 => Missing entry should be 11 - 2 - 1 - 5 - 1 = 2
Consider column R1, the missing elements should add up to 17 - 5 - 4 - 1 = 7 (3 + 4 or 4 + 3) ----(1)
Consider R5, the missing elements should add up to 10 => 2 + 4 + 4 or 4 + 3 + 3 (not possible) as (1) requires a 3.
Now, we can fill column R1 as 3 + 4 and the remaining in column R4 and we can get the complete table
R2 gave ratings of 1, 1, 2, 2, 5 => He gave 4 to 0 workers => 0 is the answer.
Q3: What rating did R1 give to Xavier?
Ans: 3
Sol: Given that the means of the ratings given by R1, R2, R3, R4 and R5 were 3.4, 2.2, 3.8, 2.8 and 3.4 respectively.
=> The sum of ratings given by R1, R2, R3 R4, R5 are 5*means = 17, 11, 19, 14, and 17 respectively.
Similarly the sum of ratings received by U, V, W, X and Y are 5*means = 11, 19, 17, 18, and 13 respectively.
Also capturing the absolute data given in the partial information (a) and (b) and representing as a table, we get:
Now,
Consider U
Given median = 2, mode = 2 and range = 3
=> His ratings should be of the form 1, a , 2, b, 4 => 1 + 2 + 4 + a + b = 11 => a + b = 4. For mode = 2 => a = b = 2
=> U's ratings are 1, 2, 2, 2, 4.
Consider V
Given median = 4, mode = 4 and range = 3
=> His ratings should be of the form 2, a, 4, b, 5 => 2 + 4 + 5 + a + b = 19 => a + b = 8 => For mode = 4 => a = b = 4
=> V's ratings are 2, 4, 4, 4, 5.
Consider W
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => 1 + a + 4 + 5 + 5 = 17 => a = 2
=> W's ratings are 1, 2, 4, 5, 5.
Consider X
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => a + 1 + 4 + 5 + 5 = 18 => a = 3
=> X's ratings are 1, 3, 4, 5, 5
Consider Y
Given median = 3, mode = 1 & 4, Range = 3
=> His ratings are 1, 1, 3, 4, 4.
Capturing this data in the table, we get:
Now, consider column R3 => The two missing entries should add up to 19 - 1 - 5 - 5 = 8, (only possibility is 4 + 4) => We can fill the row "U" and 4 in the row "V"
Now, consider column R2 => Missing entry should be 11 - 2 - 1 - 5 - 1 = 2
Consider column R1, the missing elements should add up to 17 - 5 - 4 - 1 = 7 (3 + 4 or 4 + 3) ----(1)
Consider R5, the missing elements should add up to 10 => 2 + 4 + 4 or 4 + 3 + 3 (not possible) as (1) requires a 3.
Now, we can fill column R1 as 3 + 4 and the remaining in column R4 and we can get the complete table
=> From the table, we can see that R1 gave a rating of 3 to Xavier.
Q4: What is the median of the ratings given by R3 to the five workers?
Ans: 4
Sol: Given that the means of the ratings given by R1, R2, R3, R4 and R5 were 3.4, 2.2, 3.8, 2.8 and 3.4 respectively.
=> The sum of ratings given by R1, R2, R3 R4, R5 are 5*means = 17, 11, 19, 14, and 17 respectively.
Similarly the sum of ratings received by U, V, W, X and Y are 5*means = 11, 19, 17, 18, and 13 respectively.
Also capturing the absolute data given in the partial information (a) and (b) and representing as a table, we get:
Now,
Consider U
Given median = 2, mode = 2 and range = 3
=> His ratings should be of the form 1, a , 2, b, 4 => 1 + 2 + 4 + a + b = 11 => a + b = 4. For mode = 2 => a = b = 2
=> U's ratings are 1, 2, 2, 2, 4.
Consider V
Given median = 4, mode = 4 and range = 3
=> His ratings should be of the form 2, a, 4, b, 5 => 2 + 4 + 5 + a + b = 19 => a + b = 8 => For mode = 4 => a = b = 4
=> V's ratings are 2, 4, 4, 4, 5.
Consider W
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => 1 + a + 4 + 5 + 5 = 17 => a = 2
=> W's ratings are 1, 2, 4, 5, 5.
Consider X
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => a + 1 + 4 + 5 + 5 = 18 => a = 3
=> X's ratings are 1, 3, 4, 5, 5
Consider Y
Given median = 3, mode = 1 & 4, Range = 3
=> His ratings are 1, 1, 3, 4, 4.
Capturing this data in the table, we get:
Now, consider column R3 => The two missing entries should add up to 19 - 1 - 5 - 5 = 8, (only possibility is 4 + 4) => We can fill the row "U" and 4 in the row "V"
Now, consider column R2 => Missing entry should be 11 - 2 - 1 - 5 - 1 = 2
Consider column R1, the missing elements should add up to 17 - 5 - 4 - 1 = 7 (3 + 4 or 4 + 3) ----(1)
Consider R5, the missing elements should add up to 10 => 2 + 4 + 4 or 4 + 3 + 3 (not possible) as (1) requires a 3.
Now, we can fill column R1 as 3 + 4 and the remaining in column R4 and we can get the complete table
=> Ratings give by R3 are 1, 4, 4, 5, 5 => Median = 4.
Q5: Which among the following restaurants gave its median rating to exactly one of the workers?
(a) R2
(b) R5
(c) R4
(d) R3
Ans: c
Sol: Given that the means of the ratings given by R1, R2, R3, R4 and R5 were 3.4, 2.2, 3.8, 2.8 and 3.4 respectively.
=> The sum of ratings given by R1, R2, R3 R4, R5 are 5*means = 17, 11, 19, 14, and 17 respectively.
Similarly the sum of ratings received by U, V, W, X and Y are 5*means = 11, 19, 17, 18, and 13 respectively.
Also capturing the absolute data given in the partial information (a) and (b) and representing as a table, we get:
Now,
Consider U
Given median = 2, mode = 2 and range = 3
=> His ratings should be of the form 1, a , 2, b, 4 => 1 + 2 + 4 + a + b = 11 => a + b = 4. For mode = 2 => a = b = 2
=> U's ratings are 1, 2, 2, 2, 4.
Consider V
Given median = 4, mode = 4 and range = 3
=> His ratings should be of the form 2, a, 4, b, 5 => 2 + 4 + 5 + a + b = 19 => a + b = 8 => For mode = 4 => a = b = 4
=> V's ratings are 2, 4, 4, 4, 5.
Consider W
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => 1 + a + 4 + 5 + 5 = 17 => a = 2
=> W's ratings are 1, 2, 4, 5, 5.
Consider X
Given median = 4, mode = 5 and range = 4
=> His ratings should be of the form 1, a, 4, 5, 5 => a + 1 + 4 + 5 + 5 = 18 => a = 3
=> X's ratings are 1, 3, 4, 5, 5
Consider Y
Given median = 3, mode = 1 & 4, Range = 3
=> His ratings are 1, 1, 3, 4, 4.
Capturing this data in the table, we get:
Now, consider column R3 => The two missing entries should add up to 19 - 1 - 5 - 5 = 8, (only possibility is 4 + 4) => We can fill the row "U" and 4 in the row "V"
Now, consider column R2 => Missing entry should be 11 - 2 - 1 - 5 - 1 = 2
Consider column R1, the missing elements should add up to 17 - 5 - 4 - 1 = 7 (3 + 4 or 4 + 3) ----(1)
Consider R5, the missing elements should add up to 10 => 2 + 4 + 4 or 4 + 3 + 3 (not possible) as (1) requires a 3.
Now, we can fill column R1 as 3 + 4 and the remaining in column R4 and we can get the complete table
=> R2 median rating is 2 => given to 2 workers
=> R5 median rating is 4 => given to 2 workers
=> R4 median rating is 3 => given to only 1 worker.
=> R3 median rating is 4 => given to 2 workers.
2022
Passage - 1
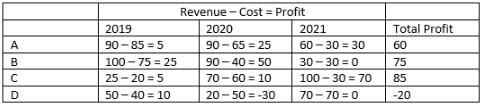
The two plots below show data for four companies code-named A, B, C, and D over three years - 2019, 2020, and 2021.
The first plot shows the revenues and costs incurred by the companies during these years. For example, in 2021, company C earned Rs.100 crores in revenue and spent Rs.30 crores. The profit of a company is defined as its revenue minus its costs.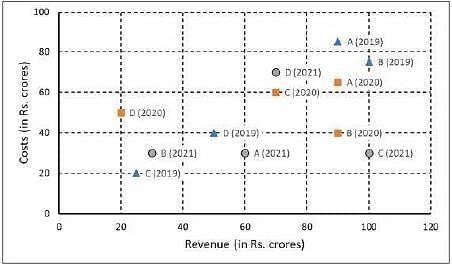
The second plot shows the number of employees employed by the company (employee strength) at the start of each of these three years, as well as the number of new employees hired each year (new hires). For example, Company B had 250 employees at the start of 2021, and 30 new employees joined the company during the year.
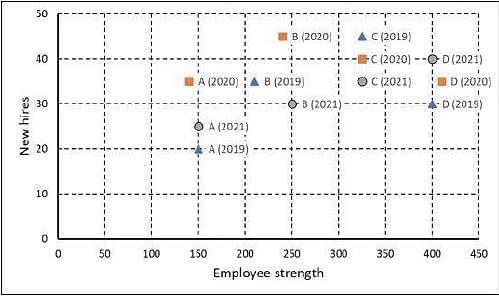 Q1: Considering all three years, which company had the highest annual profit?
Q1: Considering all three years, which company had the highest annual profit?
(a) Company B
(b) Company C
(c) Company D
(d) Company A
Ans: b
Sol:
Company C had the highest annual profit considering all 3 years.
Q2: Which of the four companies experienced the highest annual loss in any of the years?
(a) Company B
(b) Company C
(c) Company A
(d) Company D
Ans: d
Sol:
Company D experienced the highest annual loss of 30 in 2020.
Q3: The ratio of a company’s annual profit to its annual costs is a measure of its performance. Which of the four companies had the lowest value of this ratio in 2019?
(a) Company D
(b) Company C
(c) Company B
(d) Company A
Ans: d
Sol:
In 2019, profit/cost = performance
5/85 (Company A) is the lowest
Q4: The total number of employees lost in 2019 and 2020 was the least for:
(a) Company D
(b) Company B
(c) Company A
(d) Company C
Ans: b
Sol:
Employees lost in the years 2019 and 2020 = {ES in 2020 – (ES + NH) in 2019} + {ES in 2021 – (ES + NH) in 2020} = {ES in 2021 – ES in 2019 – NH in (2019 + 2020)}
[ES = Employee Strength; NH = New Hires]
A: 150 – 150 – (20 + 35) = -55
B: 250 – 210 – (35 + 45) = -40
C: 325 – 325 – (45 + 40) = -85
D: 400 – 400 – (30 + 35) = -65
[-ve denotes loss]
The lowest loss is for Company B (40 employees)
Q5: Profit per employee is the ratio of a company’s profit to its employee strength. For this purpose, the employee strength in a year is the average of the employee strength at the beginning of that year and the beginning of the next year. In 2020, which of the four companies had the highest profit per employee?
(a) Company C
(b) Company B
(c) Company A
(d) Company D
Ans: b
Sol:
A: 25/(140+150)/2 = 50/290
B: 50/(240+250)/2 = 100/490
C: 10/(325+325)/2 = 20/650
B (100/490) > A (100/580)
Hence, B had the highest profit per employee
Passage - 2
In the following, a year corresponds to 1st of January of that year.
A study to determine the mortality rate for a disease began in 1980. The study chose 1000 males and 1000 females and followed them for forty years or until they died, whichever came first. The 1000 males chosen in 1980 consisted of 250 each of ages 10 to less than 20, 20 to less than 30, 30 to less than 40, and 40 to less than 50. The 1000 females chosen in 1980 also consisted of 250 each of ages 10 to less than 20, 20 to less than 30, 30 to less than 40, and 40 to less than 50.
The four figures below depict the age profile of those among the 2000 individuals who were still alive in 1990, 2000, 2010, and 2020. The blue bars in each figure represent the number of males in each age group at that point in time, while the pink bars represent the number of females in each age group at that point in time. The numbers next to the bars give the exact numbers being represented by the bars. For example, we know that 230 males among those tracked and who were alive in 1990 were aged between 20 and 30.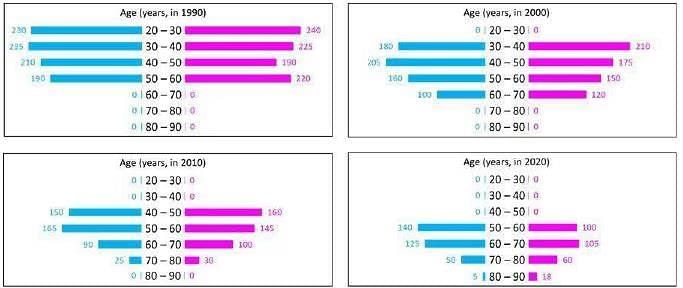 Q1: In 2000, what was the ratio of the number of dead males to dead females among those being tracked?
Q1: In 2000, what was the ratio of the number of dead males to dead females among those being tracked?
(a) 41 : 43
(b) 71 : 69
(c) 109 : 107
(d) 129 : 131
Ans: b
Sol:
There were 1000 males and females each to start with.
In 2000, males left = 180 + 205 + 160 + 100 = 645
& females left = 210 + 175 + 150 + 120 = 655
So, ratio of dead males to dead females = 355 : 345 = 71 : 69
Q2: How many people who were being tracked and who were between 30 and 40 years of age in 1980 survived until 2010?
(a) 310
(b) 110
(c) 190
(d) 90
Ans: c
Sol:
People who were in the 30-40 age group in 1980 will be in the 60-70 age group in 2010.
The sum of those people will be the answer = 90 + 100 = 190
Q3: How many individuals who were being tracked and who were less than 30 years of age in 1980 survived until 2020?
(a) 470
(b) 240
(c) 230
(d) 580
Ans: a
Sol:
The age groups considered were 10-20, 20-30, 30-40 and 40-50
The age groups that will be less than 30 years in 1980 are 10-20 and 20-30.
These age group people, after 40 years (1980 to 2020) will come in the age group of 40-50 and 50-60.
So, the number of such people (refer graph 4) = 140 + 100 + 125 + 105 = 470
Q4: How many of the males who were being tracked and who were between 20 and 30 years of age in 1980 died in the period 2000 to 2010?
Ans: 40
Sol:
Males who were in the 20-30 age group in 1980 will be in 40-50 age group in 2000 (i) and 50-60 age group in 2010 (ii).
The difference between (i) and (ii) will be the answer = 205 – 165 = 40
Q5: How many of the females who were being tracked and who were between 20 and 30 years of age in 1980 died between the ages of 50 and 60?
Ans: 30
Sol: The total number of male and female test cases in 1980 = 1000.

We are given that there are 250 females from age 20-30 in 1980 and in 2000 these females age are from 40-50 but only 175 are alive in 2000.
In 2000 there were 175 females from age 40-50. If we assume that out of these, 30 females were of age 48 years in 2000 and they died in 2005, then there are 30 females who died at the age of 53.If we assume that out of the 175 females, 30 females were of age 42 years in 2000, and they died in 2005, then 30 females died at the age of 47. Now, if we assume that there are 15 females of age 42 and 15 females of age 48 in the year 2000, and they all died in 2005, then we have 15 females who died at the age of 47 and 15 females who died at the age of 53.
So we can see that there are many cases possible. We are given that there were 250 females aged 20-30 in 1980, and in 2010, these females ages are from 50-60, but only 145 are alive in 2010.
In 2010 there were 145 females from age 50-60. If we assume that out of these, 40 females were of age 58 years in 2010 and they died in 2015, then there are 40 females who died at the age of 63.
If we assume that out of the 145 females, 40 females are of age 52 years age in 2010, and they died in 2015, then 40 females died at the age of 57. Now, if we assume that there are 15 females of age 52 and 25 females of age 58 in the year 2010, and they all died in 2015, then we have 15 females who died at the age of 57 and 25 females who died at the age of 63.
So we can see that again, there are many cases possible. In the first case, the range of values possible is from 0 to 30. In the
second case, the range of values possible is from 0 to 40. So in total, we get a range of possible values from 0 to 70.
2021
Passage - 1
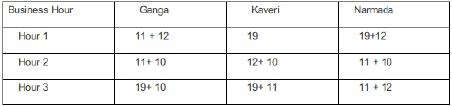
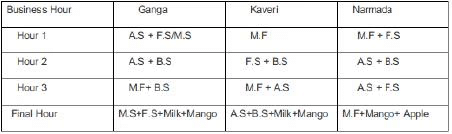
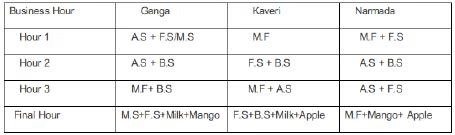
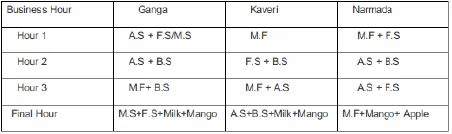
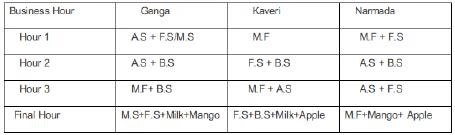
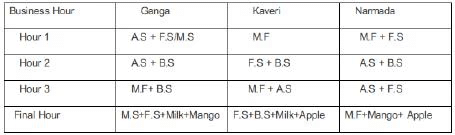
Ganga, Kaveri, and Narmada are three women who buy four raw materials (Mango, Apple, Banana and Milk) and sell five finished products (Mango smoothie, Apple smoothie, Banana smoothie, Mixed fruit smoothie and Fruit salad). Table-1 gives information about the raw materials required to produce the five finished products. One unit of a finished product requires one unit of each of the raw materials mentioned in the second column of the table.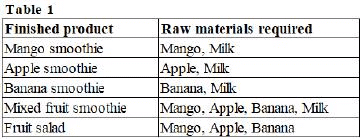
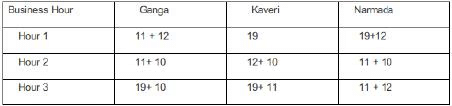
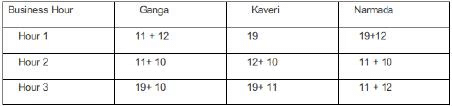
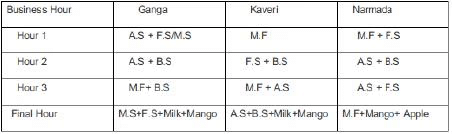
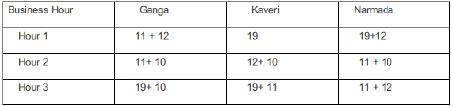
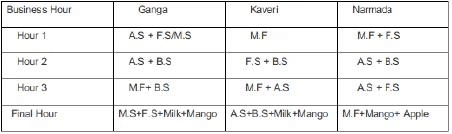
One unit of milk, mango, apple, and banana cost ₹5, ₹3, ₹2, and ₹1 respectively. Each unit of a finished product is sold for a profit equal to two times the number of raw materials used to make that product. For example, apple smoothie is made with two raw materials (apple and milk) and will be sold for a profit of ₹4 per unit. Leftover raw materials are sold during the last business hour of the day for a loss of ₹1 per unit. The amount, in rupees, received from sales (revenue) for each woman in each of the four business hours of the day is given in Table-2.
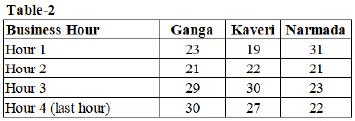
The following additional facts are known.
Each woman sold either zero or one unit of any single finished product in any hour.
- Each woman had exactly one unit each of two different raw materials as leftovers.
- No one had any banana leftover.
- No one except possibly Ganga sold any Mango smoothie.
Q1: What BEST can be concluded about the number of units of fruit salad sold in the first hour?
(a) Either 1 or 2.
(b) Either 0 or 1 or 2.
(c) Exactly 2.
(d) Exactly 1.
Ans: a
Sol: sales distribution is given by :Additionally, it has been mentioned that no one except Ganga possibly sold Mango smoothies.Considering Apple Smoothie : (AS), Mango Smoothie : ( M.S), Banana Smoothie : (B. S), Mixed Fruit : (M.F), Fruit Salad : (F.S)
In the last one hour everyone had one unit each of two different materials as leftovers: Each leftover item is sold at Re1 less than their cost price. Hence One unit of milk, mango, and apple will cost ₹4, ₹2, ₹1, The three possible combinations for the last hour in which raw materials can be sold is :One unit of milk+ One unit of mango = Rs 4+2 = Rs 6.
One unit of milk+ One unit of apple = Rs 4+1 = Rs 5.
One unit of mango+ One unit of apple = Rs 2+1 = Rs 3.
In the last one hour : Total sale of Ganga is Rs 30.
This is the total cost earned by considering selling the finished items and raw materials : Hence the possible cases are : (24 + 6) or (25 + 5) or ( 27 + 3). It is not possible to earn 25 and 27 by selling finished products.
Hence she earns Rs 24 which is possible by selling one ( M.S + F.S) and one raw unit of milk and mango each. Total sale of Kaveri is Rs 27. This is the total cost earned by considering selling the finished items and raw materials:
Hence the possible cases are : (21 + 6) or (22+5) or (24+3).
Since Kaveri cannot sell mango smoothies the possible cases are : (21+6) Selling one apple smoothie and one banana smoothie and one raw unit of Milk and Mango. (22+5) Selling one Banana smoothie and Fruit Salad, one unit of raw milk, and one unit of Raw Apple.
Total sale for Narmada is Rs 22. The possible cases are : (16+6), (17+5), (19+3).
Among these, the only possible case is 19 + 3.
Selling one unit Mixed Fruit, and one raw unit of Mango and Apple.
Case 1 :case 2 :
In the first one hour, either one or two fruit salads are sold.
Q2: Which of the following is NECESSARILY true?
(a) Ganga did not sell any leftover mangoes.
(b) Ganga did not sell any leftover apples.
(c) Narmada sold one unit of leftover milk.
(d) Kaveri sold one unit of leftover mangoes.
Ans: b
Sol: sales distribution is given by :Additionally, it has been mentioned that no one except Ganga possibly sold Mango smoothies. Considering Apple Smoothie : (AS), Mango Smoothie : ( M.S), Banana Smoothie : (B. S), Mixed Fruit : (M.F), Fruit Salad : (F.S)
In the last one hour everyone had one unit each of two different materials as leftovers: Each leftover item is sold at Re1 less than their cost price. Hence One unit of milk, mango, and apple will cost ₹4, ₹2, ₹1, The three possible combinations for the last hour in which raw materials can be sold is : One unit of milk+ One unit of mango = Rs 4+2 = Rs 6.
One unit of milk+ One unit of apple = Rs 4+1 = Rs 5.
One unit of mango+ One unit of apple = Rs 2+1 = Rs 3.
In the last one hour : Total sale of Ganga is Rs 30.
This is the total cost earned by considering selling the finished items and raw materials : Hence the possible cases are : (24 + 6) or (25 + 5) or ( 27 + 3). It is not possible to earn 25 and 27 by selling finished products.
Hence she earns Rs 24 which is possible by selling one ( M.S + F.S) and one raw unit of milk and mango each. Total sale of Kaveri is Rs 27. This is the total cost earned by considering selling the finished items and raw materials:
Hence the possible cases are : (21 + 6) or (22+5) or (24+3).
Since Kaveri cannot sell mango smoothies the possible cases are : (21+6) Selling one apple smoothie and one banana smoothie and one raw unit of Milk and Mango. (22+5) Selling one Banana smoothie and Fruit Salad, one unit of raw milk, and one unit of Raw Apple.
Total sale for Narmada is Rs 22. The possible cases are : (16+6), (17+5), (19+3).
Among these, the only possible case is 19 + 3.
Selling one unit Mixed Fruit, and one raw unit of Mango and Apple.
Case 1 :case 2 :
In both, cases Ganga did not sell any leftover apples. The other options are not necessarily true.
Q3: What BEST can be concluded about the total number of units of milk the three women had in the beginning?
(a) Either 19 or 20 units.
(b) Either 18 or 19 or 20 units.
(c) Either 18 or 19 units.
(d) Either 17 or 18 or 19 units.
Ans: b
Sol: sales distribution is given by :Additionally, it has been mentioned that no one except Ganga possibly sold Mango smoothies. Considering Apple Smoothie : (AS), Mango Smoothie : ( M.S), Banana Smoothie : (B. S), Mixed Fruit : (M.F), Fruit Salad : (F.S)
In the last one hour everyone had one unit each of two different materials as leftovers: Each leftover item is sold at Re1 less than their cost price. Hence One unit of milk, mango, and apple will cost ₹4, ₹2, ₹1, The three possible combinations for the last hour in which raw materials can be sold is :One unit of milk+ One unit of mango = Rs 4+2 = Rs 6.
One unit of milk+ One unit of apple = Rs 4+1 = Rs 5.
One unit of mango+ One unit of apple = Rs 2+1 = Rs 3.
In the last one hour : Total sale of Ganga is Rs 30.
This is the total cost earned by considering selling the finished items and raw materials : Hence the possible cases are : (24 + 6) or (25 + 5) or (27 + 3). It is not possible to earn 25 and 27 by selling finished products.
Hence she earns Rs 24 which is possible by selling one ( M.S + F.S) and one raw unit of milk and mango each. Total sale of Kaveri is Rs 27. This is the total cost earned by considering selling the finished items and raw materials:
Hence the possible cases are : (21 + 6) or (22+5) or (24+3).
Since Kaveri cannot sell mango smoothies the possible cases are : (21+6) Selling one apple smoothie and one banana smoothie and one raw unit of Milk and Mango. (22+5) Selling one Banana smoothie and Fruit Salad, one unit of raw milk, and one unit of Raw Apple.
Total sale for Narmada is Rs 22. The possible cases are : (16+6), (17+5), (19+3).
Among these, the only possible case is 19 + 3.
Selling one unit Mixed Fruit, and one raw unit of Mango and Apple.
Case 1 :Case 2 :
In except fruit salad, all the other finished products require one unit of milk :For case 1: a minimum of 19 units of milk and a maximum of 20 units of milk can be used.For case 2: a minimum of 18 units of milk and a maximum of 19 units of milk is used
Q4: If it is known that three leftover units of mangoes were sold during the last business hour of the day, how many apple smoothies were sold during the day?
Ans: 6
Sol: sales distribution is given by :Additionally, it has been mentioned that no one except Ganga possibly sold Mango smoothies. Considering Apple Smoothie : (AS), Mango Smoothie : ( M.S), Banana Smoothie : (B. S), Mixed Fruit : (M.F), Fruit Salad : (F.S)
In the last one hour everyone had one unit each of two different materials as leftovers: Each leftover item is sold at Re1 less than their cost price. Hence One unit of milk, mango, and apple will cost ₹4, ₹2, ₹1, The three possible combinations for the last hour in which raw materials can be sold is :One unit of milk+ One unit of mango = Rs 4+2 = Rs 6.
One unit of milk+ One unit of apple = Rs 4+1 = Rs 5.
One unit of mango+ One unit of apple = Rs 2+1 = Rs 3.
In the last one hour : Total sale of Ganga is Rs 30.
This is the total cost earned by considering selling the finished items and raw materials : Hence the possible cases are : (24 + 6) or (25 + 5) or ( 27 + 3). It is not possible to earn 25 and 27 by selling finished products.
Hence she earns Rs 24 which is possible by selling one ( M.S + F.S) and one raw unit of milk and mango each. Total sale of Kaveri is Rs 27. This is the total cost earned by considering selling the finished items and raw materials:
Hence the possible cases are : (21 + 6) or (22+5) or (24+3).
Since Kaveri cannot sell mango smoothies the possible cases are : (21+6) Selling one apple smoothie and one banana smoothie and one raw unit of Milk and Mango. (22+5) Selling one Banana smoothie and Fruit Salad, one unit of raw milk, and one unit of Raw Apple.
Total sale for Narmada is Rs 22. The possible cases are : (16+6), (17+5), (19+3).
Among these, the only possible case is 19 + 3.
Selling one unit Mixed Fruit, and one raw unit of Mango and Apple.
Case 1 :case 2 :
3 units of leftover mangoes were available in case 1 and in here a total of 6 apple shakes were sold.
Passage - 2
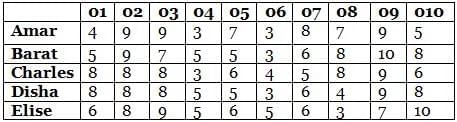
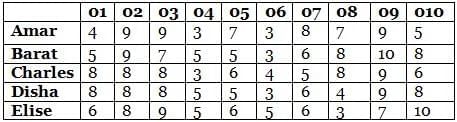
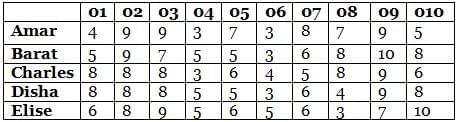
Ten objects o1, o2, …, o10 were distributed among Amar, Barat, Charles, Disha, and Elise. Each item went to exactly one person. Each person got exactly two of the items, and this pair of objects is called her/his bundle.
The following table shows how each person values each object.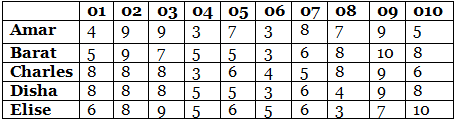 The value of any bundle by a person is the sum of that person’s values of the objects in that bundle. A person X envies another person Y if X values Y’s bundle more than X’s own bundle.
The value of any bundle by a person is the sum of that person’s values of the objects in that bundle. A person X envies another person Y if X values Y’s bundle more than X’s own bundle.
For example, hypothetically suppose Amar’s bundle consists of o1 and o2, and Barat’s bundle consists of o3 and o4. Then Amar values his own bundle at 4 + 9 = 13 and Barat’s bundle at 9 + 3 = 12. Hence Amar does not envy Barat. On the other hand, Barat values his own bundle at 7 + 5 = 12 and Amar’s bundle at 5 + 9 = 14. Hence Barat envies Amar.
The following facts are known about the actual distribution of the objects among the five people.
1. If someone’s value for an object is 10, then she/he received that object.
2. Objects o1, o2, and o3 were given to three different people.
3. Objects o1 and o8 were given to different people.
4. Three people value their own bundles at 16. No one values her/his own bundle at a number higher than 16.
5. Disha values her own bundle at an odd number. All others value their own bundles at an even number.
6. Some people who value their own bundles less than 16 envy some other people who value their own bundle at 16. No one else envies others.
Q1: What BEST can be said about object o8?
A: o8 was given to Amar, Charles, or Disha
B: o8 was given to Disha
C: o8 was given to Charles
D: o8 was given to Charles or Disha
Ans: c
Sol: We have the following table:
o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat - o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discardedCase 2: Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat - o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha.
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
So o8 is given to Charu.
Q2: What is Amar’s value for his own bundle?
Ans: 12
Sol: We have the following table:
o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat - o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discardedCase 2: Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat - o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha.
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
Amar's own valuation = 9+3 =12
Q3: Object o5 was given to
A: Disha
B: Elise
C: Amar
D: Charles
Ans: b
Sol: We have the following table:
o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat - o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discardedCase 2: Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat - o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha.
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
o5 is given to Elise
Q4: Who among the following envies someone else?
A: Barat
B: Charles
C: Amar
D: Elise
Ans: c
Sol: We have the following table:
o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat - o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discardedCase 2: Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat - o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha.
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following:
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
So Amar envies someone else
Q5: Object o4 was given to
A: Elise
B: Barat
C: Charles
D: Disha
Ans: d
Sol: We have the following table:
o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat - o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discardedCase 2: Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat - o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha.
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following:
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
o4 is given to Disha
Q6: What BEST can be said about the distribution of object o1?
A: o1 was given to Disha
B: o1 was given to Charles
C: o1 was given to Charles, Disha, or Elise
D: o1 was given to Charles or Disha
Ans: a
Sol: We have the following table:
o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat - o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discardedCase 2: Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat - o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha.
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following:
Amar - o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
So o1 is given to Disha
Passage - 3
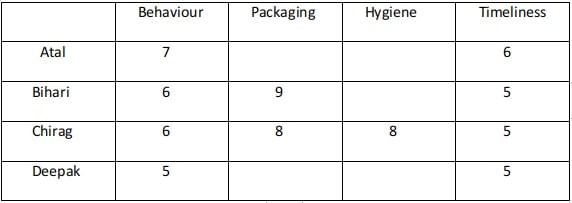
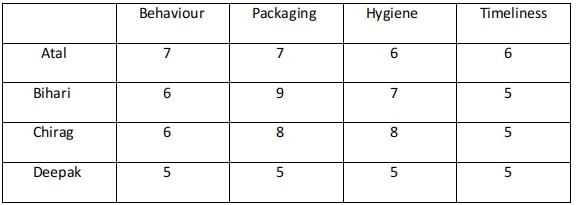
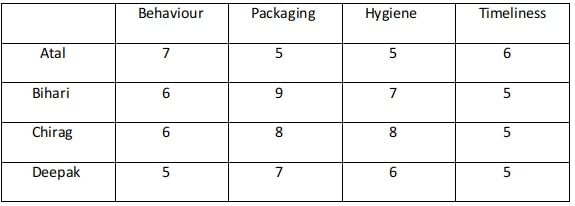
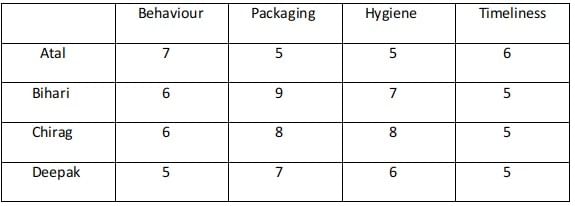
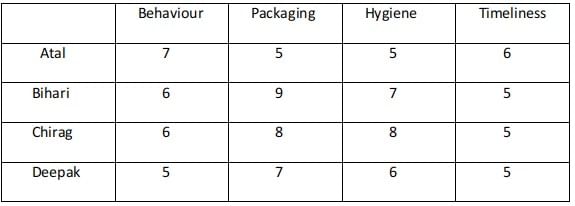
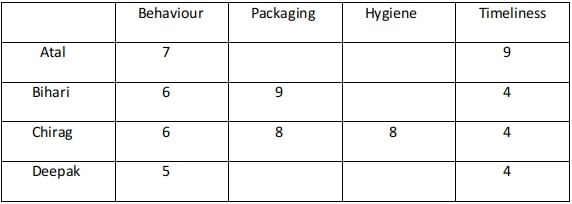
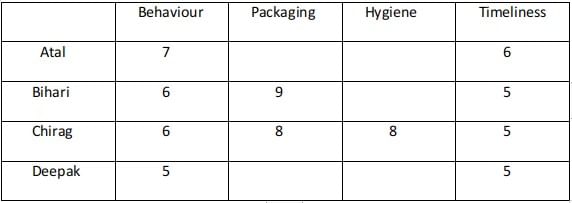
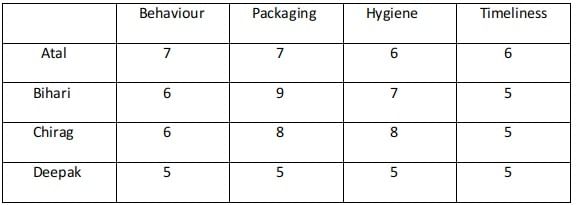
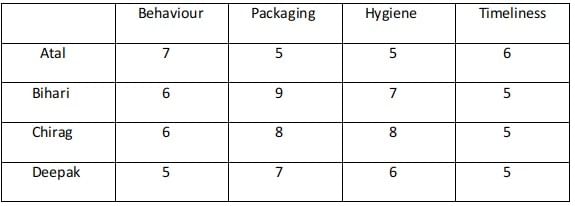
Ravi works in an online food-delivery company. After each delivery, customers rate Ravi on each of four parameters - Behaviour, Packaging, Hygiene, and Timeliness, on a scale from 1 to 9. If the total of the four rating points is 25 or more, then Ravi gets a bonus of ₹20 for that delivery. Additionally, a customer may or may not give Ravi a tip. If the customer gives a tip, it is either ₹30 or ₹50.
One day, Ravi made four deliveries - one to each of Atal, Bihari, Chirag, and Deepak, and received a total of ₹120 in bonus and tips. He did not get both a bonus and a tip from the same customer.
The following additional facts are also known.
1. In Timeliness, Ravi received a total of 21 points, and three of the customers gave him the same rating points in this parameter. Atal gave higher rating points than Bihari and Chirag in this parameter.
2. Ravi received distinct rating points in Packaging from the four customers adding up to 29 points. Similarly, Ravi received distinct rating points in Hygiene from the four customers adding up to 26 points.
3. Chirag gave the same rating points for Packaging and Hygiene.
4. Among the four customers, Bihari gave the highest rating points in Packaging, and Chirag gave the highest rating points in Hygiene.
5. Everyone rated Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
6. If the customers are ranked based on ratings given by them in individual parameters, then Atal’s rank based on Packaging is the same as that based on Hygiene. This is also true for Deepak.
Q1: What was the minimum rating that Ravi received from any customer in any parameter?
Ans: 5
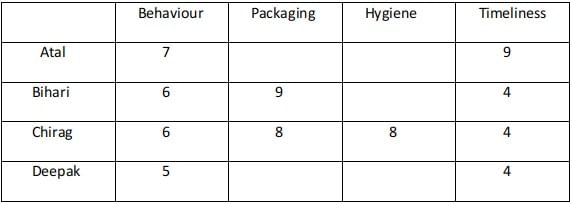
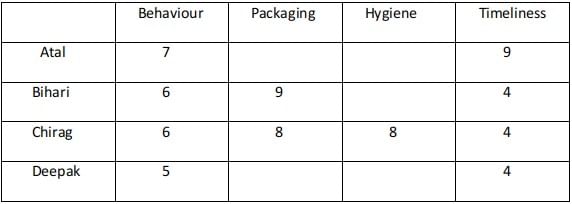
Sol: Using condition 1 :
Ravi had a total of 21 points in timeliness. 3 of the four customers among Atal, Bihari, Chirag, and Deepak gave him the same ratings. Atal gave the highest rating in timeliness in comparison with Bihari and Chirag. Hence he must have given the distinct rating.Using condition 2 :
The possibilities are A - 9, B - 4, C - 4, D - 4.
A - 6, B - 5, C - 5, D - 5.
Ravi received a total of 29 points in the Packaging and for this, the possibility of the four scores are (5, 7, 8, 9) awarded by the four customers.
In Hygiene the sum of the ratings awarded was 26. This could possibly be awarded by considering the following cases :
A-(4,6,7,9) , B-( 5,6,7,8), C-(4,5,8,9).
Using condition 4: Bihari gave the highest rating in packaging and thus Bihari must have given a 9 rating in the packaging.
Chirag gave the highest rating in Hygiene. In condition 3 it was mentioned that Chirag gave the same points for packaging and hygiene. Since 9 was rated by Bihari packaging it cannot be awarded by Chirag in packaging and hygiene. Since Chirag was awarded the highest in Hygiene.
He must award 8 points in Hygiene and Packaging.
Hence of the three possibilities among A, B, and C for Hygiene only B is the possible case with 8 as the maximum score.
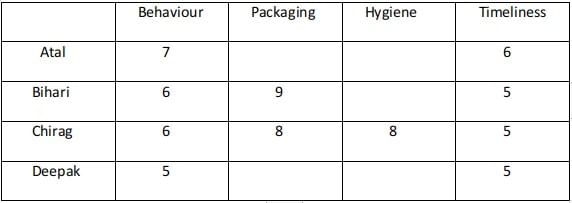
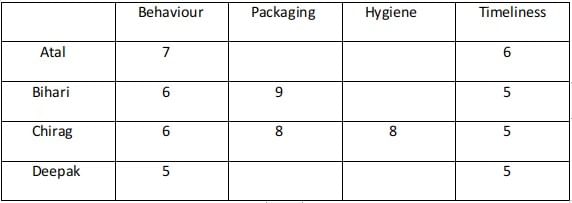
In condition 5 it was mentioned that everyone awarded Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
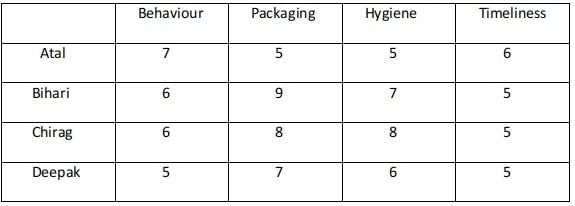
Hence Atal must have awarded 7, Deepak 6, Bihari, and Chirag 6 each in Behaviour.The two possible cases are :
Case 1 :
Case 2 :
The ratings awarded by Atal and Deepak in Packaging are among 5 and 7.The ratings awarded by Atal, Bihari, Deepak are among 5,6, and 7.
Atal individual ranking in Packaging and Hygiene are the same. The same is true for Deepak.
Since Atal and Deepak can give the ranking among 3 and 4 in Packaging as Bihari is first and Chirag is second in this parameter.
They can rank 3 or 4 in the Hygiene parameter also. Hence Bihari must rate 7 points in Hygiene.
In both the possibilities Bihari and Chirag award a total of 26 points. Hence he wins 40 because the total ratings are greater than 25 received from Bihari and Chirag.
Since he gets a total of 120 in bonuses and tips. He must have 80 from Atal and Deepak.
This is possible if he gets a tip of 30 ad 50 from them respectively.
In case 1 irrespective of Atal standing at rank 3 or rank 4 in Hygiene and Packaging Atal total rating is greater than 25 which implies Ravi gets a tip from Atal but this is not a possible case because Ravi needs a total of Rs 80 from Atal and Deepak. From Atal if he gets Rs 20 as a bonus he cannot get a total of Rs 120 and hence this case fails.
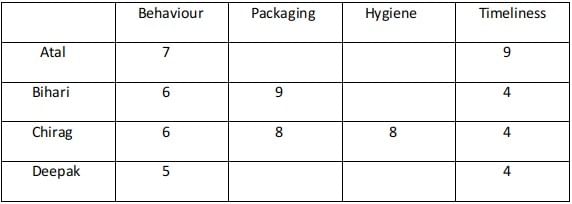
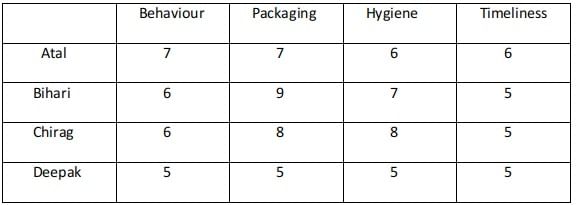
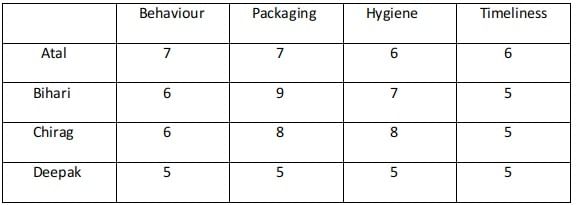
Hence case 1 fails.In case 2 there are two possibilities :
Atal ranking 3 in both the parameters and Deepak 4th. Atal ranking 4th in both the parameters and Deepak 3rd
In the case where Atal ranks 3rd in Packaging and Hygiene the total score is 26 and is not a feasible case.
Case - 2A
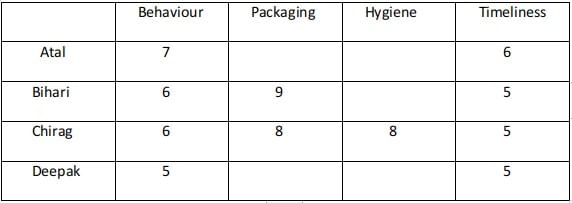
Case - 2B :
Case - 2A fails because Atal's total rating is greater than 25 which should not be the case.The minimum rating awarded is 5.
The minimum rating awarded is 5.
Q2: What rating did Atal give on Timeliness?
Ans: 6
Sol: Using condition 1 :
Ravi had a total of 21 points in timeliness. 3 of the four customers among Atal, Bihari, Chirag, and Deepak gave him the same ratings. Atal gave the highest rating in timeliness in comparison with Bihari and Chirag. Hence he must have given the distinct rating.Using condition 2 :
The possibilities are A - 9, B - 4, C - 4, D - 4.
A - 6, B - 5, C - 5, D - 5.
Ravi received a total of 29 points in the Packaging and for this, the possibility of the four scores are (5, 7, 8, 9) awarded by the four customers.
In Hygiene the sum of the ratings awarded was 26. This could possibly be awarded by considering the following cases :
A-(4,6,7,9) , B-( 5,6,7,8), C-(4,5,8,9).
Using condition 4: Bihari gave the highest rating in packaging and thus Bihari must have given a 9 rating in the packaging.
Chirag gave the highest rating in Hygiene. In condition 3 it was mentioned that Chirag gave the same points for packaging and hygiene. Since 9 was rated by Bihari packaging it cannot be awarded by Chirag in packaging and hygiene. Since Chirag was awarded the highest in Hygiene.
He must award 8 points in Hygiene and Packaging.
Hence of the three possibilities among A, B, and C for Hygiene only B is the possible case with 8 as the maximum score.
In condition 5 it was mentioned that everyone awarded Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
Hence Atal must have awarded 7, Deepak 6, Bihari, and Chirag 6 each in Behaviour.The two possible cases are :
Case 1 :
Case 2 :
The ratings awarded by Atal and Deepak in Packaging are among 5 and 7.The ratings awarded by Atal, Bihari, Deepak are among 5,6, and 7.
Atal individual ranking in Packaging and Hygiene are the same. The same is true for Deepak.
Since Atal and Deepak can give the ranking among 3 and 4 in Packaging as Bihari is first and Chirag is second in this parameter.
They can rank 3 or 4 in the Hygiene parameter also. Hence Bihari must rate 7 points in Hygiene.
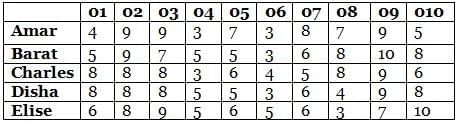
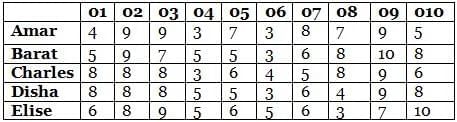
In both the possibilities Bihari and Chirag award a total of 26 points. Hence he wins 40 because the total ratings are greater than 25 received from Bihari and Chirag.
Since he gets a total of 120 in bonuses and tips. He must have 80 from Atal and Deepak.
This is possible if he gets a tip of 30 ad 50 from them respectively.
In case 1 irrespective of Atal standing at rank 3 or rank 4 in Hygiene and Packaging Atal total rating is greater than 25 which implies Ravi gets a tip from Atal but this is not a possible case because Ravi needs a total of Rs 80 from Atal and Deepak. From Atal if he gets Rs 20 as a bonus he cannot get a total of Rs 120 and hence this case fails.
Hence case 1 fails.In case 2 there are two possibilities :
Atal ranking 3 in both the parameters and Deepak 4th. Atal ranking 4th in both the parameters and Deepak 3rd
In the case where Atal ranks 3rd in Packaging and Hygiene the total score is 26 and is not a feasible case.
Case - 2A
Case - 2B :Case - 2A: fails because Atal's total rating is greater than 25 which should not be the case.
Atal has given a rating of 6 in timeliness
Q3: In which parameter did Atal give the maximum rating points to Ravi?
A: Hygiene
B: Behaviour
C: Timeliness
D: Packaging
Ans: b
Sol: Using condition 1 :
Ravi had a total of 21 points in timeliness. 3 of the four customers among Atal, Bihari, Chirag, and Deepak gave him the same ratings. Atal gave the highest rating in timeliness in comparison with Bihari and Chirag. Hence he must have given the distinct rating.Using condition 2 :
The possibilities are A - 9, B - 4, C - 4, D - 4.
A - 6, B - 5, C - 5, D - 5.
Ravi received a total of 29 points in the Packaging and for this, the possibility of the four scores are (5, 7, 8, 9) awarded by the four customers.
In Hygiene the sum of the ratings awarded was 26. This could possibly be awarded by considering the following cases :
A-(4,6,7,9) , B-( 5,6,7,8), C-(4,5,8,9).
Using condition 4: Bihari gave the highest rating in packaging and thus Bihari must have given a 9 rating in the packaging.
Chirag gave the highest rating in Hygiene. In condition 3 it was mentioned that Chirag gave the same points for packaging and hygiene. Since 9 was rated by Bihari packaging it cannot be awarded by Chirag in packaging and hygiene. Since Chirag was awarded the highest in Hygiene.
He must award 8 points in Hygiene and Packaging.
Hence of the three possibilities among A, B, and C for Hygiene only B is the possible case with 8 as the maximum score.
In condition 5 it was mentioned that everyone awarded Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
Hence Atal must have awarded 7, Deepak 6, Bihari, and Chirag 6 each in Behaviour.The two possible cases are :
Case 1 :
Case 2 :
The ratings awarded by Atal and Deepak in Packaging are among 5 and 7.The ratings awarded by Atal, Bihari, Deepak are among 5,6, and 7.
Atal individual ranking in Packaging and Hygiene are the same. The same is true for Deepak.
Since Atal and Deepak can give the ranking among 3 and 4 in Packaging as Bihari is first and Chirag is second in this parameter.
They can rank 3 or 4 in the Hygiene parameter also. Hence Bihari must rate 7 points in Hygiene.
In both the possibilities Bihari and Chirag award a total of 26 points. Hence he wins 40 because the total ratings are greater than 25 received from Bihari and Chirag.
Since he gets a total of 120 in bonuses and tips. He must have 80 from Atal and Deepak.
This is possible if he gets a tip of 30 ad 50 from them respectively.
In case 1 irrespective of Atal standing at rank 3 or rank 4 in Hygiene and Packaging Atal total rating is greater than 25 which implies Ravi gets a tip from Atal but this is not a possible case because Ravi needs a total of Rs 80 from Atal and Deepak. From Atal if he gets Rs 20 as a bonus he cannot get a total of Rs 120 and hence this case fails.
Hence case 1 fails.In case 2 there are two possibilities :
Atal ranking 3 in both the parameters and Deepak 4th. Atal ranking 4th in both the parameters and Deepak 3rd
In the case where Atal ranks 3rd in Packaging and Hygiene the total score is 26 and is not a feasible case.
Case - 2A
Case - 2B :Case - 2A: fails because Atal's total rating is greater than 25 which should not be the case.
Atal has given the maximum rating in Behaviour.
Q4: The COMPLETE list of customers who gave the maximum total rating points to Ravi is
A: Atal
B: Bihari
C: Bihari and Chirag
D: Atal and Bihari
Ans: c
Sol: Using condition 1 :
Ravi had a total of 21 points in timeliness. 3 of the four customers among Atal, Bihari, Chirag, and Deepak gave him the same ratings. Atal gave the highest rating in timeliness in comparison with Bihari and Chirag. Hence he must have given the distinct rating.Using condition 2 :
The possibilities are A - 9, B - 4, C - 4, D - 4.
A - 6, B - 5, C - 5, D - 5.
Ravi received a total of 29 points in the Packaging and for this, the possibility of the four scores are (5, 7, 8, 9) awarded by the four customers.
In Hygiene the sum of the ratings awarded was 26. This could possibly be awarded by considering the following cases :
A-(4,6,7,9) , B-( 5,6,7,8), C-(4,5,8,9).
Using condition 4: Bihari gave the highest rating in packaging and thus Bihari must have given a 9 rating in the packaging.
Chirag gave the highest rating in Hygiene. In condition 3 it was mentioned that Chirag gave the same points for packaging and hygiene. Since 9 was rated by Bihari packaging it cannot be awarded by Chirag in packaging and hygiene. Since Chirag was awarded the highest in Hygiene.
He must award 8 points in Hygiene and Packaging.
Hence of the three possibilities among A, B, and C for Hygiene only B is the possible case with 8 as the maximum score.
In condition 5 it was mentioned that everyone awarded Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
Hence Atal must have awarded 7, Deepak 6, Bihari, and Chirag 6 each in Behaviour.The two possible cases are :
Case 1 :
Case 2 :
The ratings awarded by Atal and Deepak in Packaging are among 5 and 7.The ratings awarded by Atal, Bihari, Deepak are among 5,6, and 7.
Atal individual ranking in Packaging and Hygiene are the same. The same is true for Deepak.
Since Atal and Deepak can give the ranking among 3 and 4 in Packaging as Bihari is first and Chirag is second in this parameter.
They can rank 3 or 4 in the Hygiene parameter also. Hence Bihari must rate 7 points in Hygiene.
In both the possibilities Bihari and Chirag award a total of 26 points. Hence he wins 40 because the total ratings are greater than 25 received from Bihari and Chirag.
Since he gets a total of 120 in bonuses and tips. He must have 80 from Atal and Deepak.
This is possible if he gets a tip of 30 ad 50 from them respectively.
In case 1 irrespective of Atal standing at rank 3 or rank 4 in Hygiene and Packaging Atal total rating is greater than 25 which implies Ravi gets a tip from Atal but this is not a possible case because Ravi needs a total of Rs 80 from Atal and Deepak. From Atal if he gets Rs 20 as a bonus he cannot get a total of Rs 120 and hence this case fails.
Hence case 1 fails.In case 2 there are two possibilities :
Atal ranking 3 in both the parameters and Deepak 4th. Atal ranking 4th in both the parameters and Deepak 3rd
In the case where Atal ranks 3rd in Packaging and Hygiene the total score is 26 and is not a feasible case.
Case - 2A
Case - 2B :Case - 2A : fails because Atal's total rating is greater than 25 which should not be the case.
Bihari and Chirag has given the highest ratings
Q5: What BEST can be concluded about the tip amount given by Deepak?
A: Either ₹0 or ₹30 or ₹50
B: Either ₹30 or ₹50
C: ₹50
D: ₹30
Ans: b
Sol: Using condition 1 :
Ravi had a total of 21 points in timeliness. 3 of the four customers among Atal, Bihari, Chirag, and Deepak gave him the same ratings. Atal gave the highest rating in timeliness in comparison with Bihari and Chirag. Hence he must have given the distinct rating.Using condition 2 :
The possibilities are A - 9, B - 4, C - 4, D - 4.
A - 6, B - 5, C - 5, D - 5.
Ravi received a total of 29 points in the Packaging and for this, the possibility of the four scores are (5, 7, 8, 9) awarded by the four customers.
In Hygiene the sum of the ratings awarded was 26. This could possibly be awarded by considering the following cases :
A-(4,6,7,9) , B-( 5,6,7,8), C-(4,5,8,9).
Using condition 4: Bihari gave the highest rating in packaging and thus Bihari must have given a 9 rating in the packaging.
Chirag gave the highest rating in Hygiene. In condition 3 it was mentioned that Chirag gave the same points for packaging and hygiene. Since 9 was rated by Bihari packaging it cannot be awarded by Chirag in packaging and hygiene. Since Chirag was awarded the highest in Hygiene.
He must award 8 points in Hygiene and Packaging.
Hence of the three possibilities among A, B, and C for Hygiene only B is the possible case with 8 as the maximum score.
In condition 5 it was mentioned that everyone awarded Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
Hence Atal must have awarded 7, Deepak 6, Bihari, and Chirag 6 each in Behaviour.The two possible cases are :
Case 1 :
Case 2 :
The ratings awarded by Atal and Deepak in Packaging are among 5 and 7.The ratings awarded by Atal, Bihari, Deepak are among 5,6, and 7.
Atal individual ranking in Packaging and Hygiene are the same. The same is true for Deepak.
Since Atal and Deepak can give the ranking among 3 and 4 in Packaging as Bihari is first and Chirag is second in this parameter.
They can rank 3 or 4 in the Hygiene parameter also. Hence Bihari must rate 7 points in Hygiene.
In both the possibilities Bihari and Chirag award a total of 26 points. Hence he wins 40 because the total ratings are greater than 25 received from Bihari and Chirag.
Since he gets a total of 120 in bonuses and tips. He must have 80 from Atal and Deepak.
This is possible if he gets a tip of 30 ad 50 from them respectively.
In case 1 irrespective of Atal standing at rank 3 or rank 4 in Hygiene and Packaging Atal total rating is greater than 25 which implies Ravi gets a tip from Atal but this is not a possible case because Ravi needs a total of Rs 80 from Atal and Deepak. From Atal if he gets Rs 20 as a bonus he cannot get a total of Rs 120 and hence this case fails.
Hence case 1 fails.In case 2 there are two possibilities :
Atal ranking 3 in both the parameters and Deepak 4th. Atal ranking 4th in both the parameters and Deepak 3rd
In the case where Atal ranks 3rd in Packaging and Hygiene the total score is 26 and is not a feasible case.
Case - 2A
Case - 2B :Case - 2A: fails because Atal's total rating is greater than 25 which should not be the case.
Among Atal and Deepak, one of them gives a tip of 30 and the other gives a tip of 50. Hence 30 or 50 any case is possible
Q6: What rating did Deepak give on Packaging?
A: 7
B: 8
C: 5
D: 6
Ans: a
Sol: Using condition 1 :
Ravi had a total of 21 points in timeliness. 3 of the four customers among Atal, Bihari, Chirag, and Deepak gave him the same ratings. Atal gave the highest rating in timeliness in comparison with Bihari and Chirag. Hence he must have given the distinct rating.Using condition 2 :
The possibilities are A - 9, B - 4, C - 4, D - 4.
A - 6, B - 5, C - 5, D - 5.
Ravi received a total of 29 points in the Packaging and for this, the possibility of the four scores are (5, 7, 8, 9) awarded by the four customers.
In Hygiene the sum of the ratings awarded was 26. This could possibly be awarded by considering the following cases :
A-(4,6,7,9) , B-( 5,6,7,8), C-(4,5,8,9).
Using condition 4: Bihari gave the highest rating in packaging and thus Bihari must have given a 9 rating in the packaging.
Chirag gave the highest rating in Hygiene. In condition 3 it was mentioned that Chirag gave the same points for packaging and hygiene. Since 9 was rated by Bihari packaging it cannot be awarded by Chirag in packaging and hygiene. Since Chirag was awarded the highest in Hygiene.
He must award 8 points in Hygiene and Packaging.
Hence of the three possibilities among A, B, and C for Hygiene only B is the possible case with 8 as the maximum score.
In condition 5 it was mentioned that everyone awarded Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
Hence Atal must have awarded 7, Deepak 6, Bihari, and Chirag 6 each in Behaviour.The two possible cases are :
Case 1 :
Case 2 :
The ratings awarded by Atal and Deepak in Packaging are among 5 and 7.The ratings awarded by Atal, Bihari, Deepak are among 5,6, and 7.
Atal individual ranking in Packaging and Hygiene are the same. The same is true for Deepak.
Since Atal and Deepak can give the ranking among 3 and 4 in Packaging as Bihari is first and Chirag is second in this parameter.
They can rank 3 or 4 in the Hygiene parameter also. Hence Bihari must rate 7 points in Hygiene.
In both the possibilities Bihari and Chirag award a total of 26 points. Hence he wins 40 because the total ratings are greater than 25 received from Bihari and Chirag.
Since he gets a total of 120 in bonuses and tips. He must have 80 from Atal and Deepak.
This is possible if he gets a tip of 30 ad 50 from them respectively.
In case 1 irrespective of Atal standing at rank 3 or rank 4 in Hygiene and Packaging Atal total rating is greater than 25 which implies Ravi gets a tip from Atal but this is not a possible case because Ravi needs a total of Rs 80 from Atal and Deepak. From Atal if he gets Rs 20 as a bonus he cannot get a total of Rs 120 and hence this case fails.
Hence case 1 fails.In case 2 there are two possibilities :
Atal ranking 3 in both the parameters and Deepak 4th. Atal ranking 4th in both the parameters and Deepak 3rd
In the case where Atal ranks 3rd in Packaging and Hygiene the total score is 26 and is not a feasible case.
Case - 2A
Case - 2B :Case - 2A : fails because Atal's total rating is greater than 25 which should not be the case.
Deepak gives a rating of 7 in Packaging.
|
77 videos|180 docs|96 tests
|
FAQs on Tables CAT Previous Year Questions with Answer PDF
| 1. What types of tables are commonly found in CAT exams? |  |
| 2. How can I effectively interpret data from tables in the exam? |  |
| 3. What strategies can I use to solve table-based questions quickly? |  |
| 4. Are there any common mistakes to avoid when working with tables in the exam? |  |
| 5. How important are tables in the overall scoring of the exam? |  |