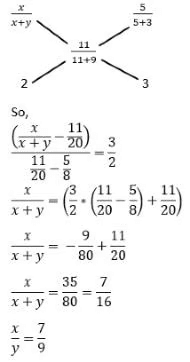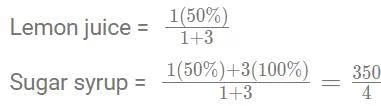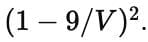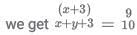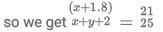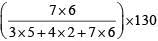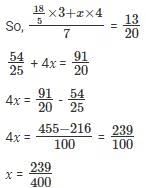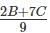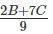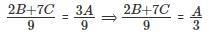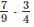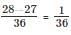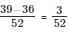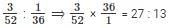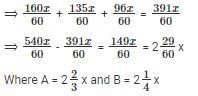Mixtures & Alligations CAT Previous Year Questions with Answer PDF
From 2016 to 2024, 22 questions on mixtures and alligations appeared in CAT Quant, usually 1–2 questions per year. These included ratio-based mixing, repeated replacement, and profit/loss using alligation or weighted averages, ranging from moderate to difficult.
2024
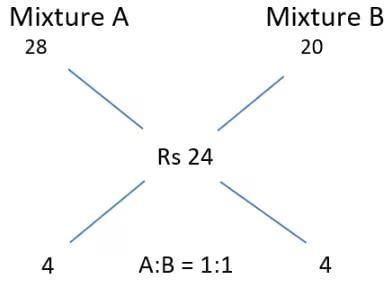
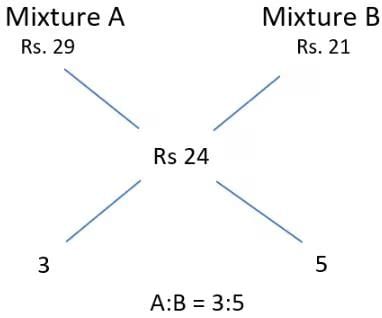
Q1: Rajesh and Vimal own 20 hectares and 30 hectares of agricultural land, respectively, which are entirely covered by wheat and mustard crops. The cultivation area of wheat and mustard in the land owned by Vimal are in the ratio of 5 : 3. If the total cultivation area of wheat and mustard are in the ratio 11 : 9, then the ratio of cultivation area of wheat and mustard in the land owned by Rajesh is
(a) 1 : 1
(b) 4 : 3
(c) 7 : 9
(d) 3 : 7
Ans: c
Sol: According to the question,
Rajesh: 20 hectares
Vimal: 30 hectares
The entire land is cultivated by 2 crops i.e., wheat and mustard
We have, cultivation area of wheat and mustard on Vimal’s land = 5: 3
Total cultivation area of wheat and mustard = 11: 9
So, for finding the cultivation area of wheat and mustard on Rajesh’s land here, we can use the concept of alligation, (Assume the ratio to be x: y)
Hence, the ratio of cultivation area of wheat and mustard in the land owned by Rajesh = 7: 9
2023
Q1: A mixture P is formed by removing a certain amount of coffee from a coffee jar and replacing the same amount with cocoa powder. The same amount is again removed from mixture P and replaced with same amount of cocoa powder to form a new mixture Q. If the ratio of coffee and cocoa in the mixture Q is 16 : 9, then the ratio of cocoa in mixture P to that in mixture Q is [2023]
(a) 4 : 9
(b) 1 : 3
(c) 5 : 9
(d) 1 : 2
Ans: (c)
Sol:
Q2: A container has 40 liters of milk. Then, 4 liters are removed from the container and replaced with 4 liters of water. This process of replacing 4 liters of the liquid in the container with an equal volume of water is continued repeatedly. The smallest number of times of doing this process, after which the volume of milk in the container becomes less than that of water, is
Ans: 7
Sol:
2022
Q1: A mixture contains lemon juice and sugar syrup in equal proportion. If a new mixture is created by adding this mixture and sugar syrup in the ratio 1 : 3, then the ratio of lemon juice and sugar syrup in the new mixture is [2022]
(a) 1 : 4
(b) 1 : 5
(c) 1 : 6
(d) 1 : 7
Ans: (d)
Sol: Lemon juice : sugar syrup in the mixture is 1:1, i.e. 50% Lemon juice and 50% sugar syrup.
In sugar syrup, 100% is sugar syrup.
These two are mixed in the ratio 1:3.
Required ratio = 50 : 350 = 1 : 7
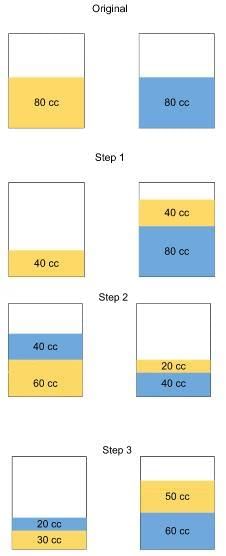
Q2: There are two containers of the same volume, first container half-filled with sugar syrup and the second container half-filled with milk. Half the content of the first container is transferred to the second container, and then the half of this mixture is transferred back to the first container. Next, half the content of the first container is transferred back to the second container. Then the ratio of sugar syrup and milk in the second container is [2022]
(a) 5 : 6
(b) 5 : 4
(c) 6 : 5
(d) 4 : 5
Ans: (a)
Sol: We know that the process of shifting half volumes is happening three times overall.
So it would be wise to assume the initial volume to be some multiple of 8 so that we don’t have to deal with fractions later on.
The ratio of Sugar Syrup to Water in the second container is 50/60 which is equal to 5:6
2021
Q1: The strength of an indigo solution in percentage is equal to the amount of indigo in grams per 100 cc of water. Two 800 cc bottles are filled with indigo solutions of strengths 33% and 17%, respectively. A part of the solution from the first bottle is thrown away and replaced by an equal volume of the solution from the second bottle. If the strength of the indigo solution in the first bottle has now changed to 21% then the volume, in cc, of the solution left in the second bottle is [2021]
Ans: 200
Sol: Target = 21%. Apply alligation between 33% and 17%.So, to achieve this, we must replace 600 cc from A with 600 cc from B.
Left in B = 800 – 600 = 200.
Q2: From a container filled with milk, 9 litres of milk are drawn and replaced with water. Next, from the same container, 9 litres are drawn and again replaced with water. If the volumes of milk and water in the container are now in the ratio of 16 : 9, then the capacity of the container, in litres, is
Ans: 45
Sol:Let capacity = V.
Fraction left after 2 rounds =
Given = 16/25.Answer = 45 L.
Q3: A box has 450 balls, each either white or black, there being as many metallic white balls as metallic black balls. If 40% of the white balls and 50% of the black balls are metallic, then the number of non-metallic balls in the box is
Ans: 250
Sol: Let the number of white balls be x and black balls be y
So we get x+y =450 ....(1)
Now metallic black balls = 0.5y
Metallic white balls = 0.4x
From condition 0.4x=0.5y
we get 4x-5y=0 ....(2)
Solving (1) and (2), we get
x=250 and y =200
Now number of Non Metallic balls = 0.6x+0.5y = 150+100 = 250
Q4: A person buys tea of three different qualities at ₹ 800, ₹ 500, and ₹ 300 per kg, respectively, and the amounts bought are in the proportion 2 : 3 : 5. She mixes all the tea and sells one-sixth of the mixture at ₹ 700 per kg. The price, in INR per kg, at which she should sell the remaining tea, to make an overall profit of 50%, is
(a) 653
(b) 688
(c) 692
(d) 675
Ans: b
Sol: Considering the three kinds of tea are A, B, and C.
The price of kind A = Rs 800 per kg.
The price of kind B = Rs 500 per kg.
The price of kind C = Rs 300 per kg.
They were mixed in the ratio of 2 : 3: 5. 1/6 of the total mixture is sold for Rs 700 per kg.
Assuming the ratio of mixture to A = 12kg, B = 18kg, and C =30 kg.Take the total = 60 kg (12 + 18 + 30).
Cost = 800×12 + 500×18 + 300×30 = 27,600.
Need 50% profit ⇒ revenue = 41,400.Already earned = 700×10 = 7,000.
The remaining 50 kg must earn 34,400.
Priceper kg = 34.400/50 = 688.
Q5: If a certain weight of an alloy of silver and copper is mixed with 3 kg of pure silver, the resulting alloy will have 90% silver by weight. If the same weight of the initial alloy is mixed with 2 kg of another alloy which has 90% silver by weight, the resulting alloy will have 84% silver by weight. Then, the weight of the initial alloy, in kg, is
(a) 3.5
(b) 2.5
(c) 3
(d) 4
Ans: c
Sol: Let the alloy contain x Kg silver and y kg copper
Now when mixed with 3Kg Pure silverwe get 10x+30 =9x+9y+27
9y-x=3 (1)
Now as per condition 2 silver in 2nd alloy = 2(0.9) =1.8we get 21y-4x =3 (2)
solving (1) and (2) we get y= 0.6 and x =2.4
so x+y = 3
2020
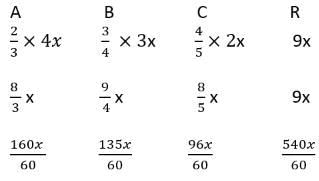
Q1: An alloy is prepared by mixing three metals A, B and C in the proportion 3: 4: 7 by volume. Weights of the same volume of the metals A, B and C are in the ratio 5: 2: 6. In 130 kg of the alloy, the weight, in kg, of the metal C is [2020]
(a) 70
(b) 96
(c) 48
(d) 84
Ans: (d)
Sol: Required weight of C =
= 84 kg
Q2: A solution, of volume 40 litres, has dye and water in the proportion 2 : 3. Water is added to the solution to change this proportion to 2 : 5. If one-fourths of this diluted solution is taken out, how many litres of dye must be added to the remaining solution to bring the proportion back to 2 : 3? [2020]
Ans: 8
Sol: Original quantity of dye and water in the original solution i.e., 16 litresand 24 litres (i.e. = 40 - 16)
Quantity of water added = 16 litres (As 1 part = 8 litres). Quantity of dye and water
removed =i.e., 4 litres and
i.e., 10 litres. Final quantity of dye and
water is 12 litres and 30 litres.
∴ Quantity of dye to be added to make the ratio of dye and water again 2: 3 i.e., 8 litres.
2019
Q1: A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is [2019]
(a) 70
(b) 85
(c) 80
(d) 75
Ans: (c)
Sol: In Liquid L1 - 1L = 1000 grams
So, 1000 mL = 1000 grams
1 mL = 1 gram
x mL = x grams
In Liquid L2 - 1L = 800 grams
1000 mL = 800 grams
1mL = 0.8 grams
(500-x) mL = (500-x) x 0.8 grams
Total mass = x + 400 - 0.8x = 480 grams
0.2x = 80 grams
x = 400 grams
Therefore, Liquid 1 has 400 mL and Liquid 2 has 500 - 400 = 100 Ml
Therefore, Percentage of Liquid 1 = (400/500) x 100 = 80%
Q2: The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is [2019]
(a) 15
(b) 12
(c) 13
(d) 14
Ans: (d)
Sol:Salt in A=50, B=110, C=160.
Step 1: A→B (100 mL, 10% = 10 g). A=40, B=120.
Step 2: B→C (100 mL, 20% = 20 g). B=100, C=180.
Step 3: C→A (100 mL, 30% = 30 g). C=150, A=70.
So A has 70/500=14%.
Answer = 14%.
2018
Q1: A trader sells 10 litres of a mixture of paints A and B, where the amount of B in the mixture does not exceed that of A. The cost of paint A per litre is Rs. 8 more than that of paint B. If the trader sells the entire mixture for Rs. 264 and makes a profit of 10%, then the highest possible cost of paint B, in Rs. per litre, is [2018]
(a) 20
(b) 16
(c) 22
(d) 26
Ans: (a)
Sol: Given, The amount of B in mixture ≤ Amount of A in mixture
Selling Price = Rs. 264 and Profit = 10 %
264 = 1.1 × CP
CP = (264/1.1) = Rs. 240 for 10 litres
CP per litre = Rs. 24
We also know that, CP per litre of A = CP per litre of B + 8 Let CP per litre of B = x So, CP per litre of A = x + 8
Given Amount of B ≤ Amount of A,
Maximum possible cost of B occurs when B = A
We need to choose values for A and B in such a way that the quantities remain same.But A should be 8 more than B
Therefore, A should have a CP per litre of Rs. 28 and B should have a CP per litre of Rs 20
B cannot be assigned any more than this as the amount of B would become more than A
Example: Let us assign B to be Rs. 21 and A to be Rs. 29 which would result in a ratio of 3:5 where B amounts more than A, which doesn’t satisfy the condition
Max possible cost of Paint B = Rs. 20 per litre
Q2: A wholesaler bought walnuts and peanuts, the price of walnut per kg being thrice that of peanut per kg. He then sold 8 kg of peanuts at a profit of 10% and 16 kg of walnuts at a profit of 20% to a shopkeeper. However, the shopkeeper lost 5 kg of walnuts and 3 kg of peanuts in transit. He then mixed the remaining nuts and sold the mixture at Rs. 166 per kg, thus making an overall profit of 25%. At what price, in Rs. per kg, did the wholesaler buy the walnuts? [2018]
(a) 84
(b) 86
(c) 96
(d) 98
Ans: (c)
Sol: Let the wholesaler bought walnuts and peanuts at Rs 3x and Rs x respectively
He sold 8kgs of Peanuts to the shopkeeper at 10% Profit
Cost price of the Peanuts bought by the shopkeeper = Rs. 1.1x per kg
Similarly, he sold 16 kgs of Walnuts to the shopkeeper at 20% Profit
Cost price of the Walnuts bought by the shopkeeper = 1.2 × 3x = Rs. 3.6x per Kg
He lost 5 kgs of Walnuts and 3 Kgs of Peanuts in transit
Remaining = 16 - 5 = 11 kgs of Walnuts & 8-3 = 5 kgs of Peanuts
He mixes them together and sells them at Rs. 166 per kg, making an overall Profit of 25%
Selling Price = 5/4 × Cost Price
Overall Cost Price = Rs.(3.6 × 16x + 1.1 × 8x)
Overall Selling Price = Rs. 16 × 166
Overall Selling Price = (5/4) x Overall Cost Price
(3.6 × 16x + 1.1 × 8x) × (5/4) = 16 × 166
((57.6 × 8.8) x ) × 5/4 = 16 × 166
x = Rs. 32
Cost price per Kg of Walnuts bought by the Wholesaler = Rs. 3x = 3 × 32 = >Rs. 96
Q3: There are two drums, each containing a mixture of paints A and B. In drum 1, A and B are in the ratio 18 : 7. The mixtures from drums 1 and 2 are mixed in the ratio 3 : 4 and in this final mixture, A and B are in the ratio 13 : 7. In drum 2, then A and B were in the ratio [2018]
(a) 251 : 163
(b) 239 : 161
(c) 220 : 149
(d) 229 : 141
Ans: b
Sol:
Given that two drums each containing a mixture of paints A and B. In drum 1, A and B are in the ratio 18 : 7. Drums 1 and 2 are mixed in the ratio 3 : 4 and in the final mixture A and B are in the ratio 13 : 7. For these kinds of questions do not consider separately as A and B. Deal with either A or B as a share of overall
Here A is (18/25) of overall
In D2, let us assume the proportion of A with respect to the overall mixture is x. 3 parts of D1 is mixed with parts of D2 to give proportion of A of which is (13/20)th of the overall mixture. From here on, it is weighted averages.
In drum 2, A is (239/400) so B should be the remaining. Therefore, A : B = 239 : 161.
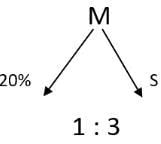
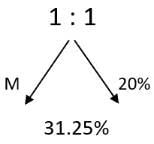
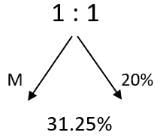
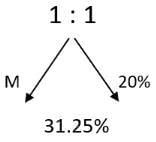
Q4: A 20% ethanol solution is mixed with another ethanol solution, say, S of unknown concentration in the proportion 1:3 by volume. This mixture is then mixed with an equal volume of 20% ethanol solution. If the resultant mixture is a 31.25% ethanol solution, then the unknown concentration of S is [2018]
(a) 50%
(b) 55%
(c) 48%
(d) 52%
Ans: (a)
Sol: Given that 20% ethanol solution is mixed with another ethanol solution, say, S of unknown concentration in the proportion 1:3 by volume
This M is then mixed with an equal volume of 20% ethanol solution. If the resultant mixture is a 31.25% ethanol solution ,then the unknown concentration of S has to be found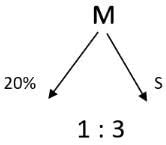
Equal quantities of mixture and 20% ethanol solution are mixed in equal ratio to get 31.25%
The mixture and 20% ethanol solution are mixed in equal ratio to get 31.25%. This 31.25% is 11.25% more than this 20%. This mixture must be 11.25% more than 31.25% so mixture is equal to 42.5%
This mixture 42.5% is mixed in the ratio 1:3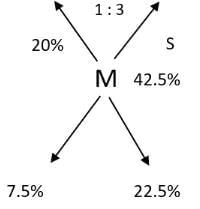
Using allegations we can find this 22.5% which should be in the ratio 1:3 so the other one is 7.5%
S = 42.5 + 7.5
S = 50%
Here to find the solution, do the second thing first and then go to the first thing
The second one is mixed in the ratio 1 : 1 so that the final thing should be bang in the middle
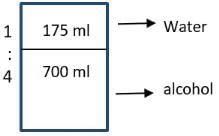
Q5: A jar contains a mixture of 175 ml water and 700 ml alcohol. Gopal takes out 10% of the mixture and substitutes it by water of the same amount. The process is repeated once again. The percentage of water in the mixture is now [2018]
(a) 25.4
(b) 20.5
(c) 30.3
(d) 35.2
Ans: (d)
Sol:Given that a jar contains a mixture of 175 ml water and 700 ml alcohol.
It is given that 10% of the mixture is removed and it is substituted by water of the same amount and the process is repeated once again
Now we have to find the percentage of water in the mixture.
Since the mixture is removed and substituted with water, we can deal with alcohol and the second step we can find how much amount of alcohol is retained and not about how much amount of alcohol is removed
As 10% of alcohol is removed, 90% of alcohol is retained
So alcohol remaining = 700 × 90% × 90%
⇒ 700 × 0.9 × 0.9 = 567
We totally have 875 ml overall mixture and of this 567 ml is alcohol.
Remaining 875 – 567 = 308 is the amount of water.
We have to find the percentage of water in the mixture i.e. 308/875
Approximately 308 is 30% of 1000 so by this we know that 308 is more than 30%
Hence 35.2% is the percentage of water in the given mixture.
Q6: The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. If three salt solutions A, B, C are mixed in the proportion 1 : 2 : 3, then the resulting solution has strength 20%. If instead the proportion is 3 : 2 : 1, then the resulting solution has strength 30%. A fourth solution, D, is produced by mixing B and C in the ratio 2 : 7. The ratio of the strength of D to that of A is [2018]
(a) 3 : 10
(b) 1 : 3
(c) 2 : 5
(d) 1 : 4
Ans: (b)
Sol: Given that the strength of the salt solution is p% if 100 ml of the solution contains p grams of salt
It is also given that three salt solutions A , B , C are mixed in the proportion 1 : 2 : 3, then the resulting solution has strength 20%.
So= 0.2 ⇒ A + 2B + 3C = 1.2 ...(1)
If instead the proportion is 3 : 2 : 1, then the resulting solution has strength 30%
So,= 0.3 ⇒ 3A +2B + C = 1.8 ...(2)
It is given that 4th solution D is produced by mixing B and C in the ratio 2 : 7
So D =
We have to find the ratio of the strength of D : A
Subtracting equations 1 and 2, we get
2A – 2C = 0.6 or A – C = 0.3
Since we could not find anything from the above methods, we can eliminate the number part and get the ratio going
A + 2B + 3C = 1.2
3A + 2B + C = 1.8
So let us multiply eqn 1 and 2 with 3 and 2,
3A + 6B + 9C = 6A + 4B + 2C
2B + 7C = 3A
It is given that D =
Hence D = A/3
Therefore the ratio D : A = 1 : 3.
2017
Q1: Bottle 1 contains a mixture of milk and water in 7 : 2 ratio and Bottle 2 contains a mixture of milk and water in 9 : 4 ratio. In what ratio of volumes should the liquids in Bottle 1 and Bottle 2 be combined to obtain a mixture of milk and water in 3 : 1 ratio? [2017]
(a) 27 : 14
(b) 27 : 13
(c) 27 : 16
(d) 27 : 18
Ans: (b)
Sol:
Bottle 1 and bottle 2 contains mixture of milk and water in the ratio 7 : 2 and 9 : 4 respectively.
We have to find by what ratio bottle 1 and Bottle 2 should be combined to obtain a mixture of milk and water in the ratio 3 : 1
For this we can consider milk to the whole mixture or else water to the whole mixture.⇒
Taking LCM we get
LCM is 52 so
Bottle 1 and 2 are mixed in the ratio 27 : 13.
Q2: Consider three mixtures - the first having water and liquid A in the ratio 1 : 2, the second having water and liquid B in the ratio 1 : 3, and the third having water and liquid C in the ratio 1 : 4. These three mixtures of A, B, and C, respectively, are further mixed in the proportion 4 : 3 : 2. Then the resulting mixture has [2017]
(a) The same amount of water and liquid B
(b) The same amount of liquids B and C
(c) More water than liquid B
(d) More water than liquid A
Ans: (c)
Sol: There are three mixtures ,the first having water and liquid A in the ratio 1 : 2,
so we can consider only the liquid part which is 2/3.
The second having the water and liquid in the ratio 1 : 3 = 3/4.
The third having the liquid and water in the ratio 1 : 4 = 4/5
Hence by this we can infer that more water than liquid B is true
|
165 videos|229 docs|95 tests
|
FAQs on Mixtures & Alligations CAT Previous Year Questions with Answer PDF
| 1. How do you calculate the mean of a mixture of substances? |  |
| 2. What is the difference between a mixture and an alloy in the context of mixtures and alligations? |  |
| 3. How can the method of alligation help in solving mixture problems? |  |
| 4. Can you explain the concept of allegations in the context of mixtures and alligations? |  |
| 5. How can one determine the percentage of each component in a given mixture using the method of alligation? |  |