Number Series CAT Previous Year Questions with Answer PDF
Introduction
- The CAT Quantitative Ability (QA) Section places a significant emphasis on Number Systems, deeming it a pivotal topic. A robust grasp of the fundamentals of CAT Number Systems is crucial, necessitating active practice engagement. Additionally, explore Number System questions from preceding CAT papers, complemented by detailed video solutions. This article delves into specific Number System questions pertinent to the CAT Exam. For CAT aspirants gearing up for one of India's most competitive management entrance exams, excelling in each section is of utmost importance.
- This document concentrates on CAT preparation, specifically honing in on the Number Systems segment. It offers a thorough review of questions from 2017 to 2024, providing step-by-step solutions and valuable insights to enhance your preparedness for success. Proficiency in Number Systems is imperative for CAT success, and this document serves as a comprehensive resource for both novices and seasoned CAT aspirants.
- It compiles past-year questions, expert tips, and strategies to aid you in mastering this challenging section. Join us on this CAT 2025 preparation journey as we dissect Number Systems, arming you with the knowledge and techniques necessary to conquer the CAT exam.
Previous Year Questions
Q1: Let n be the least positive integer such that 168 is a factor of 1134n. If m is the least positive integer such that 1134n is a factor of 168m, then m + n equals [2023]
(a) 12
(b) 9
(c) 15
(d) 24
Ans: (c)
Sol: The prime factorizations of 168 and 1134 are as follows:
168 = 23 × 3 × 7
1134 = 2 × 34 × 7
Clearly, the smallest positive integral value of n, such that 168 is a factor of 1134n is 3.
1134n = 11343 = 23 × 312 × 73
Clearly, the smallest positive integral value of m, such that 11343 is a factor of 168m is 12.
Therefore, m + n = 12 + 3 = 15
Q2: The number of all natural numbers up to 1000 with non-repeating digits is [2023]
(a) 585
(b) 504
(c) 648
(d) 738
Ans: (d)
Sol: Single digit numbers with non-repeating digits = 9
(The unit’s digit is non-zero)
Two digit numbers with non-repeating digits = 9 × 9
(The tenth’s digit is non-zero and the unit digit can be any digit except the tenth’s digit.)
Three digit numbers with non-repeating digits = 9 × 9 × 8
(The hundred’s digit is non-zero and the tenth’s digit can be any digit except the hundred’s digit and the unit digit can be any digit except the tenth’s digit.)
So, totally there are (9 + 9 × 9 + 9 × 9 × 8) = 738 natural numbers up to 1000 with non-repeating digits.
Q3: For any natural numbers m, n, and k, such that k divides both m + 2n and 3m + 4n, k must be a common divisor of [2023]
(a) 2m and 3n
(b) m and 2n
(c) 2m and n
(d) m and n
Ans: (b)
Sol: k divides m + 2n
So, k also divides 2(m + 2n) = 2m + 4n
It is given that k divides 3m + 4n
Which means, k should also divide (3m + 4n) – (2m + 4n)
∴k divides m
Since k divides m and m + 2n
k should also divide (m + 2n) – m = 2n
Therefore, k divides m and 2n.
Q4: The number of positive integers less than 50, having exactly two distinct factors other than 1 and itself, is [2023]
Sol: A positive integer less than 50, having exactly two distinct factors other than 1 and itself, is either a perfect cube below 50 or an integer that is a product of exactly two distinct primes.
Case i)
Perfect cubes below 50 are 23 and 33. So, two numbers here
Case ii)
For the product of two primes to be below 50, the individual primes should be below 25.
(Because, the smallest prime is 2 and multiplying 2 with anything greater than or equal to 25 yields a number greater than or equal to 50.)
2, 3, 5, 7, 11, 13, 17, 19, 23 are prime numbers less than 25.
2, 3, 5, 7 are the primes less than √, any product of two numbers among them yields a product less than 50.
So, there are 4C2 pairs here.
11, 13, 17, 19, 23 are the primes greater than √, any product of two numbers among them yields a product greater than 50.
So, there are 0 pairs here.
Between the two lists 11 and 13 can pair with 2 and 3, while 17, 19, and 23 can only pair with 2.
So, there are 7 pairs here.
So, totally, there are 2 + 6 + 0 + 7 = 15 such numbers.
Q5: A school has less than 5000 students and if the students are divided equally into teams of either 9 or 10 or 12 or 25 each, exactly 4 are always left out. However, if they are divided into teams of 11 each, no one is left out. The maximum number of teams of 12 each that can be formed out of the students in the school is [2022]
Sol: Since the total number of students, when divided by either 9 or 10 or 12 or 25 each, gives a remainder of 4, the number will be in the form of LCM(9,10,12,25)k + 4 = 900k + 4.
It is given that the value of 900k + 4 is less than 5000.
Also, it is given that 900k + 4 is divided by 11.
It is only possible when k = 2 and total students = 1804.
So, the number of 12 students group = 1800/12 = 150.
Q6: Consider six distinct natural numbers such that the average of the two smallest numbers is 14, and the average of the two largest numbers is 28. Then, the maximum possible value of the average of these six numbers is [2022]
(a) 23
(b) 24
(c) 23.5
(d) 22.5
Ans: (d)
Sol: Let the six numbers be a, b, c, d, e, f in ascending order
a + b = 28
e + f = 56
If we want to maximise the average then we have to maximise the value of c and d and maximise e and minimise f
e + f = 56
As e and f are distinct natural numbers so possible values are 27 and 29
Therefore c and d will be 25 and 26 respecitively
So average = 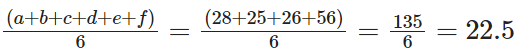
Q7: For some natural number n, assume that (15,000)! is divisible by (n!)!. The largest possible value of n is [2022]
(a) 4
(b) 7
(c) 6
(d) 5
Ans: (b)
Sol: To find the largest possible value of n, we need to find the value of n such that n! is less than 15000.
7! = 5040
8! = 40320 > 15000
This implies 15000! is not divisible by 40320!
Therefore, maximum value n can take is 7.
The answer is option B.
Q8: How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7? [2020]
Sol: Let the number be ‘abc’. Then, 2 < a × b × c < 7. The product can be 3, 4, 5, 6.
We can obtain each of these as products with the combination 1,1, x where x = 3, 4, 5, 6.
Each number can be arranged in 3 ways, and we have 4 such numbers: hence, a total of 12 numbers fulfilling the criteria.
We can factories 4 as 2*2 and the combination 2,2,1 can be used to form 3 more distinct numbers.
We can factorize 6 as 2*3 and the combination 1,2,3 can be used to form 6 additional distinct numbers.
Thus a total of 12 + 3 + 6 = 21 such numbers can be formed.
Q9: The mean of all 4-digit even natural numbers of the form ‘aabb’,where a > 0, is [2020]
(a) 4466
(b) 5050
(c) 4864
(d) 5544
Ans: (d)
Sol: The four digit even numbers will be of form:
1100, 1122, 1144 … 1188, 2200, 2222, 2244 … 9900, 9922, 9944, 9966, 9988
Their sum ‘S’ will be (1100 + 1100 + 22 + 1100 + 44 + 1100 + 66 + 1100 + 88) + (2200 + 2200 + 22 + 2200 + 44 +…)….+ (9900 + 9900 + 22 + 9900 + 44 + 9900 + 66 + 9900 + 88)
⇒ S=1100*5 + (22+44+66+88)+2200*5+(22 + 44 + 66 + 88)….+ 9900*5 + (22 + 44 + 66 + 88)
⇒ S=5*1100(1 + 2 + 3 + …9)+9(22 + 44 + 66 + 88)
⇒ S=5*1100*9*10/2 + 9*11*20
Total number of numbers are 9*5=45
∴ Mean will be S/45 = 5*1100 + 44 = 5544.
Q10: How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3? [2020]
Sol: Here there are two cases possible
Case 1: When 7 is at the left extreme
In that case 3 can occupy any of the three remaining places and the remaining two places can be taken by (0,1,2,4,5,6,8,9)
So total ways 3(8)(7)= 168
Case 2: When 7 is not at the extremes
Here there are 3 cases possible. And the remaining two places can be filled in 7(7) ways.(Remember 0 can’t come on the extreme left)
Hence in total 3(7)(7)=147 ways
Total ways 168+147=315 ways
Q11: How many of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7? [2020]
(a) 42
(b) 41
(c) 40
(d) 43
Ans: (b)
Sol: The number of multiples of 2 between 1 and 120 = 60
The number of multiples of 5 between 1 and 120 which are not multiples of 2 = 12
The number of multiples of 7 between 1 and 120 which are not multiples of 2 and 5 = 7
Hence, number of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7 = 120 – 60 – 12 – 7 = 41
Q12: Let N, x and y be positive integers such that N = x + y, 2 < x < 10 and 14 < y < 23. If N > 25, then how many distinct values are possible for N? [2020]
Sol: Possible values of x = 3,4,5,6,7,8,9
When x = 3, there is no possible value of y
When x = 4, the possible values of y = 22
When x = 5, the possible values of y=21,22
When x = 6, the possible values of y = 20.21,22
When x = 7, the possible values of y = 19,20,21,22
When x = 8, the possible values of y=18,19,20,21,22
When x = 9, the possible values of y=17,18,19,20,21,22
The unique values of N = 26,27,28,29,30,31
Q13: How many integers in the set {100, 101, 102, …, 999} have at least one digit repeated? [2020]
Sol: Total number of numbers from 100 to 999 = 900
The number of three digits numbers with unique digits:
_ _ _
The hundredth’s place can be filled in 9 ways ( Number 0 cannot be selected)
Ten’s place can be filled in 9 ways
One’s place can be filled in 8 ways
Total number of numbers = 9*9*8 = 648
Number of integers in the set {100, 101, 102, …, 999} have at least one digit repeated = 900 – 648 = 252
Q14: What is the largest positive integer n such that 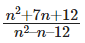 is also a positive integer? [2019]
is also a positive integer? [2019]
(a) 6
(b) 16
(c) 8
(d) 12
Ans: (d)
Sol: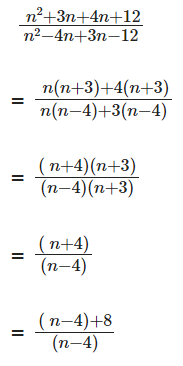
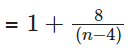
which will be maximum when n - 4 = 8
n = 12
Q15: How many pairs (m, n) of positive integers satisfy the equation m2 + 105 = n2? [2019]
Sol: n2 - m2 = 105
(n - m)(n + m) = 1*105, 3*35, 5*21, 7*15, 15*7, 21*5, 35*3, 105*1.
n - m = 1, n + m = 105 ⇒ n = 53, m = 52
n - m = 3, n + m = 35 ⇒ n = 19, m = 16
n - m = 5, n + m = 21 ⇒ n =13, m = 8
n - m = 7, n + m = 15 ⇒ n = 11, m = 4
n - m = 15, n + m = 7 ⇒ n = 11, m = -4
n - m = 21, n + m = 5 ⇒ n = 13, m = -8
n - m = 35, n + m = 3 ⇒ n = 19, m = -16
n - m = 105, n + m = 1 ⇒ n = 53, m = -52
Since only positive integer values of m and n are required. There are 4 possible solutions.
Q16: How many factors of 24 × 35 × 104 are perfect squares which are greater than 1? [2019]
Sol: 24 × 35 × 104
=24 × 35 × 24 × 54
= 28 × 35 × 54
For the factor to be a perfect square, the factor should be even power of the number.
In 28, the factors which are perfect squares are 20, 22, 24, 26, 28 = 5
Similarly, in 35, the factors which are perfect squares are 30, 32, 34 = 3
In 54, the factors which are perfect squares are 50, 52, 54 = 3
Number of perfect squares greater than 1 = 5 × 3 × 3 - 1
= 44
Q17: In a six-digit number, the sixth, that is, the rightmost, digit is the sum of the first three digits, the fifth digit is the sum of first two digits, the third digit is equal to the first digit, the second digit is twice the first digit and the fourth digit is the sum of fifth and sixth digits. Then, the largest possible value of the fourth digit is [2019]
Sol: Let the six-digit number be ABCDEF
F = A + B + C, E= A + B, C = A, B = 2A, D = E + F.
Therefore D = 2A + 2B + C = 2A + 4A + A = 7A.
A cannot be 0 as the number is a 6 digit number.
A cannot be 2 as D would become 2 digit number.
Therefore A is 1 and D is 7.
Q18: The product of two positive numbers is 616. If the ratio of the difference of their cubes to the cube of their difference is 157 : 3, then the sum of the two numbers is [2019]
(a) 58
(b) 85
(c) 50
(d) 95
Ans: (c)
Sol: Assume the numbers are a and b, then ab = 616
We have, 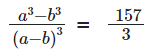
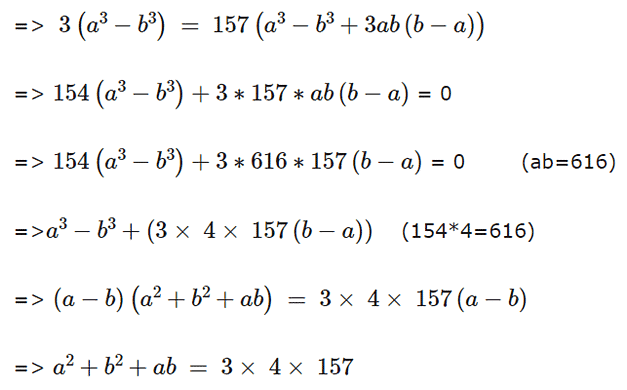
Adding ab = 616 on both sides, we get
a2 + b2 + ab + ab = 3 × 4 × 157 + 616
=> (a + b)2 = 3 × 4 × 157 + 616 = 2500
=> a + b = 50
Q19: While multiplying three real numbers, Ashok took one of the numbers as 73 instead of 37. As a result, the product went up by 720. Then the minimum possible value of the sum of squares of the other two numbers is [2018]
Sol: We know that one of the 3 numbers is 37.
Let the product of the other 2 numbers be x.
It has been given that 73x-37x = 720
36x = 720
x = 20
Product of 2 real numbers is 20.
We have to find the minimum possible value of the sum of the squares of the 2 numbers.
Let x=a*b
It has been given that a*b=20
The least possible sum for a given product is obtained when the numbers are as close to each other as possible.
Therefore, when a=b, the value of a and b will be √20.
Sum of the squares of the 2 numbers 20 + 20 = 40.
Therefore, 40 is the correct answer.
Q20: The number of integers x such that 0.25 ≤ 2x ≤ 200 and 2x + 2 is perfectly divisible by either 3 or 4, is [2018]
Sol: At x = 0, 2x = 1 which is in the given range [0.25, 200]
2x + 2 = 1 + 2 = 3 Which is divisible by 3. Hence, x 0 is one possible solution.
At x = 1, 2x = 2 which is in the given range [0.25, 200]
2x + 2 = 2 + 2 = 3 Which is divisible by 4. Hence, x = 1 is one possible solution.
At x = 2, 2x = 4 which is in the given range [0.25, 200]
2x + 2 = 4 + 2 = 6 Which is divisible by 3. Hence, x = 2 is one possible solution.
At x = 3, 2x = 8 which is in the given range [0.25, 200]
2x + 2 = 8 + 2 = 3 Which is not divisible by 3 or 4. Hence, x = 3 can't be a solution.
At x = 4, 2x = 16 which is in the given range [0.25, 200]
2x + 2 = 16 + 2 = 18 Which is divisible by 3. Hence, x 4 is one possible solution.
At x = 5, 2x = 32 which is in the given range [0.25, 200]
2x + 2 = 32 + 2 = 34 Which is not divisible by 3 or 4. Hence, x = 5 can't be a solution.
At x = 6, 2x = 64 which is in the given range [0.25, 200]
2x + 2 = 64 + 2 = 66 Which is divisible by 3. Hence, x 6 is one possible solution.
At x = 7, 2x = 128 which is in the given range [0.25, 200]
2x + 2 = 128 + 2 = 130 Which is not divisible by 3 or 4. Hence, x = 7 can't be a solution.
At x = 8, 2x = 256 which is not in the given range [0.25, 200]. Hence, x can't take any value greater than 7.
Therefore, all possible values of x = {0,1,2,4,6). Hence, we can say that 'x' can take 5 different integer values.
Q21: If the sum of squares of two numbers is 97, then which one of the following cannot be their product? [2018]
(a) -32
(b) 16
(c) 48
(d) 64
Ans: (d)
Sol: Let 'a' and 'b' are those two numbers.
⇒ a2 + b2 = 97
⇒ a2 + b2 - 2ab = 97-2ab
⇒ (ab)2 = 97-2ab
We know that (a - b)2 ≥ 0
⇒ 97 - 2ab0
⇒ ab ≤ 48.5
Hence, ab ≠ 64. Therefore, option D is the correct answer.
Q22: The smallest integer n for which 4n > 1719 holds, is closest to [2018]
(a) 37
(b) 35
(c) 33
(d) 39
Ans: (d)
Sol: 4n > 1719
16n/2 > 1719
Therefore, we can say that n/2 > 19
n > 38
Hence, option D is the correct answer.
Q23: If a, b, c and d are integers such that a + b + c + d = 30 then the minimum possible value of (a - b)2 + (a - c)2 + (a - d)2 is [2017]
Sol: For the value of given expression to be minimum, the values of a, b, c and d should be as close as possible. 30/4 = 7.5
Since each one of these are integers so values must be 8, 8, 7, 7.
On putting these values in the given expression, we get
(8 - 8)2 + (8 - 7)2 + (8 - 7)2
⇒ 1 + 1 = 2
Q24: If the product of three consecutive positive integers is 15600 then the sum of the squares of these integers is [2017]
(a) 1777
(b) 1785
(c) 1875
(d) 1877
Ans: (d)
Sol: (x-1)x(x+1) = 15600
⇒ x3 - x = 15600
The nearest cube to 15600 is 15625 = 253
We can verify that x = 25 satisfies the equation above.
Hence the three numbers are 24, 25, 26. Sum of their squares = 1877
|
87 videos|172 docs|99 tests
|
FAQs on Number Series CAT Previous Year Questions with Answer PDF
| 1. What are number series questions in the CAT exam? |  |
| 2. How can I improve my skills in solving number series questions for CAT? |  |
| 3. Are number series questions considered difficult in the CAT exam? |  |
| 4. How many number series questions can I expect in the CAT exam? |  |
| 5. What strategies can I use to solve number series questions quickly in the CAT exam? |  |

















