Daily Practice Questions CAT Previous Year Questions with Answer PDF
2022
Q1: In a class of 100 students, 73 like coffee, 80 like tea and 52 like lemonade. It may be possible that some students do not like any of these three drinks. Then the difference between the maximum and minimum possible number of students who like all the three drinks is [2022]
(a) 47
(b) 53
(c) 52
(d) 48
Ans: a
Sol: Let n, s, d and t be the number of students who likes none of the drinks, exactly one drink, exactly 2 drinks and all three drinks, respectively.
It is given,
n + s + d + t = 100 ...... (1)
s + 2d + 3t = 73 + 80 + 52
s + 2d + 3t = 205 ...... (2)
(2)-(1), we get
d + 2t - n = 105
Maximum value t can take is 52, i.e. t = 52, d = 1 and n = 0
Minimum value t can take is 5, i.e. t = 5, d = 95 and n = 0 (This also satisfies equation (1))
Difference = 52 - 5 = 47
The answer is option A.
2020
Q1: Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is [2020]
(a) 22
(b) 21
(c) 20
(d) 19
Ans: c
Sol: Now 23 students choose maths as one of their subject.This means (MPC)+ (MC) + (PC)=23 where MPC denotes students who choose all the three subjects maths, physics and chemistry and so on.
So MC + PM =5 Similarly we have PC+ MP =7
We have to find the smallest number of students choosing chemistry
For that in the first equation let PM=5 and MC=0. In the second equation this PC=2
Hence minimum number of students choosing chemistry will be (18+2)=20 Since 18 students chose all the three subjects.
2019
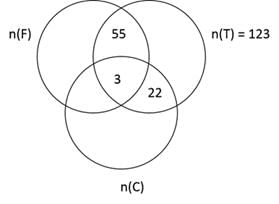
Q1: A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is [2019]
(a) 32
(b) 43
(c) 38
(d) 45
Ans: b
Sol: From observing the data given, we find that it is a closed 3 set Venn diagram.Let the three sports be F, T and C for Football, Tennis and Cricket respectivelyn(F U T U C) = 256 , n(F) = 144, n(T) = 123, n(C) = 132, n(F ∩ T) = 58, n(C ∩ T) = 25, n(F ∩ C) = 63
We know that (AUBUC) = n(A) + n(B) +n(C) - n(A ∩ B) - n(B ∩C) - n(C ∩ A) + n(A ∩ B ∩ C)So, 256 = 144 + 123 + 132 - 58 - 25 - 63 + n (F ∩ T ∩ C)n (F ∩ T ∩ C) = 256 - 144 + 123 +132 - 146n (F ∩ T ∩ C) = 256 - 253 = 3Now, it is easy to calculate the number of students who only play tennis using a Venn diagram.n (Students who play only Tennis) = 123 - (55 + 3 + 22) = 123 - 80n (Students who play only Tennis) = 43 students
2018
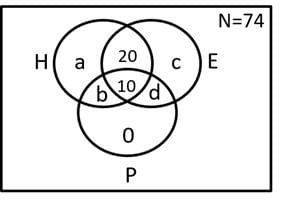
Q1: Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is [2018 TITA]
Ans: 52
Sol:
Let us draw a Three set Venn diagram from values givenSince its given that n(H) = n(E) and n(only P) = 0a + b + 20 + 10 = c + d + 20 + 10a + b = c + dAs N = 74, a + b + 20 + 10 + c + d = 742(a + b) = 44 => a + b = 22
n(H) = a + b + 20 + 10 = 22 + 20 +10 = 52 students
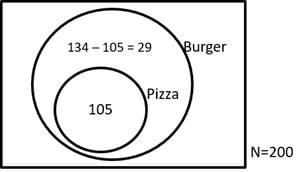
Q2: If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be [2018]
(a) 26
(b) 23
(c) 96
(d) 93
Ans: d
Sol: Given that out of 200 students, 105 like Pizza and 134 like BurgerIn order to find the possible number of students who like only Burger, we need to find the range between the minimum and maximum possible number of students
Minimum possible number of Students who like only Burger:
For this, we must try to optimize the Venn diagram in such a way that it has maximum intersection
No of Students who like only Burger = 134 – 105= 29Maximum possible number of Students who like only Burger:
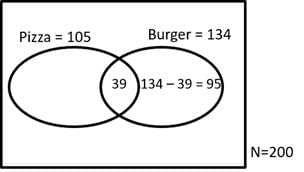
For this, we must optimize the Venn diagram in such a way that it has minimum intersection
We know that total number of Students = 200
So, Minimum number of students who like both = 105 + 134 – 200 = 39 students
Students who like Burger = 134
Max. no of Students who like only Burger = 134 – 39 = 95
So range => 29 ≤ n ≤ 95
From the options, only (D) 93 lies within range
Q3: For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1, 2, 3, 4}, Q = {2, 3, 5, 6,}, R = {1, 3, 7, 8, 9}, S = {2, 4, 9, 10}, then the number of elements in (PΔQ)Δ(RΔS) is [2018]
(a) 7
(b) 8
(c) 9
(d) 6
Ans: a
Sol:
Given that for two sets A and B, A △ B denote the set of elements which belong to A or B but not both.This is the diagram which represents A △ B ,the set of elements which belongs to A or B i.e. A intersection B subtracted from A union BWe have to find the number of elements in (P △ Q) △ (R △ S) ifP = {1 , 2 , 3 , 4} Q = {2 , 3 , 5 , 6 ,} R = {1 , 3 , 7 , 8 , 9} S = {2 , 4 , 9 , 10}For P △ Q, we have to find the elements which do not to belong to both P and Q such that(P △ Q) = {1, 4 , 5 , 6}(R △ S) = {1 , 2 , 3 , 4 , 7 , 8 , 10}(P △ Q) △ (R △ S) = {2 , 3 , 5 , 7 , 6 , 8 , 10}The number of elements (P △ Q) △ (R △ S) is 7
Q4: If A = {62n - 35n - 1: n = 1,2,3,...} and B = {35(n - 1) : n = 1, 2, 3,...} then which of the following is true? [2018]
(a) Neither every member of A is in B nor every member of B is in A
(b) Every member of A is in B and at least one member of B is not in A
(c) Every member of B is in A
(d) At least one member of A is not in B
Ans: b
Sol: Given that A = {62n - 35n - 1 : n = 1 , 2 , 3 , ...} and B = {35(n - 1) : n = 1 , 2 , 3 , ...}
A = {62n - 35n - 1}When n = 1
{62 - 35 - 1} = 0when n = 2
{64 - 35(2) - 1} = 1225when n = 3
{66 - 35(3) - 1} = 46550B = {35(n - 1) : n = 1 , 2 , 3 , ...}When n = 1{35(0)} = 0when n = 2{35(1)} = 35when n = 3{35(2)} = 70So B is more predictable here since it has every multiple of 35 ie. {0, 35, 70, 10, 140, .......}From this we can see that A is a subset of B ie. Every element of A is in B and not the vice versaTherefore every member of A is in B and at least one member of B is not in A.
|
167 videos|238 docs|95 tests
|
FAQs on Daily Practice Questions CAT Previous Year Questions with Answer PDF
| 1. What is a set in set theory? |  |
| 2. What is the cardinality of a set? |  |
| 3. How is a subset defined in set theory? |  |
| 4. What is the difference between a set and a subset? |  |
| 5. How is the union of two sets defined in set theory? |  |