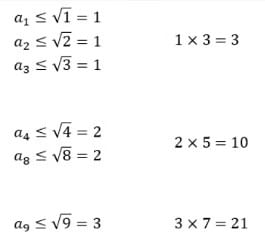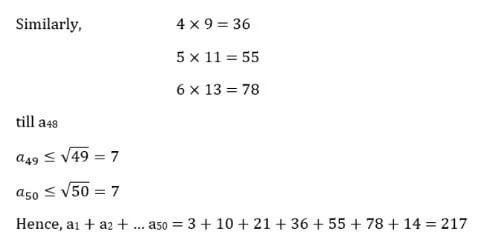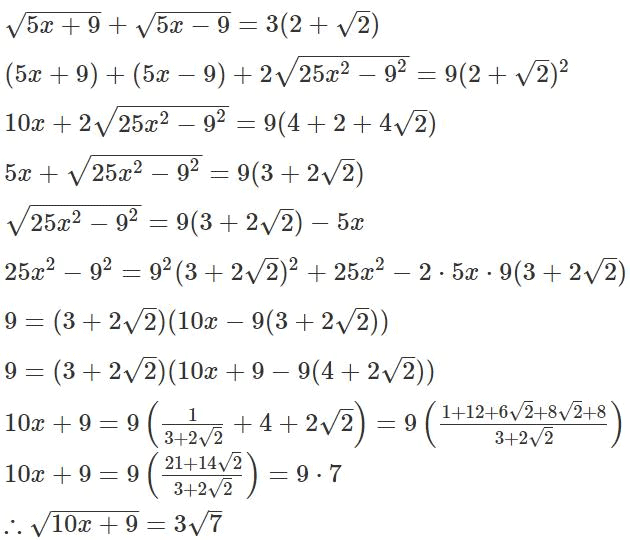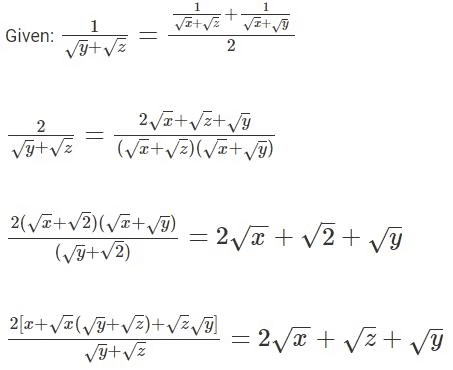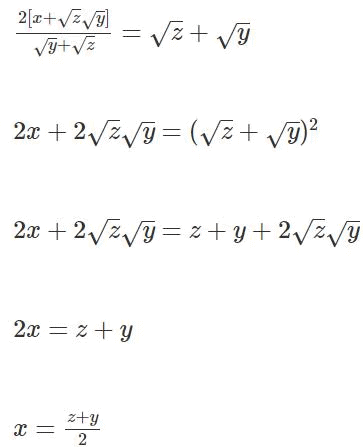CAT Exam > CAT Notes > Quantitative Aptitude (Quant) > CAT Previous Year Questions - Square Root and Cube Root
CAT Previous Year Questions - Square Root and Cube Root | Quantitative Aptitude (Quant) PDF Download
2024
Q1: If (a + b√n) is the positive square root of (29 - 12√5), where a and b are integers, and n is a natural number, then the maximum possible value of (a + b + n) is
(a) 4
(b) 18
(c) 6
(d) 22
Ans: b
Sol: So 29 - 12√5 is the positive square root of (29 - 12√5).
So 29 - 12√5 = (a + b√n)²
29 - 12√5 = a² + b²n + 2ab√n
a² + b²n = 29
ab√n = -6√5
a²b²n² = 180
b²n = 180 / a²
Substituting this in the above equation:
a² + b²n = 29
a² + (180 / a²) = 29
a⁴ - 29a² + 180 = 0
a² = (29 ± √(29² - 4*180)) / 2
a² = 9 or 20
That means one of a² or b²n is 9 or 20.
We also have ab√n = -6√5; that means one of a or b should be negative.
And also the fact that this is a positive root, and we need to maximize the value of a, b, and n.
We can have a = -3, b = 1, and n = 20.
This satisfies all the above equations, and the value of a + b + n = 18
Q2: For any natural number n, let an be the largest integer not exceeding √n. Then the value of a1 + a2 + a3 + ... + a50 is
Ans: 217
Sol:
2023
Q1: If 
then 
is equal to
(a) 4√5
(b) 2√7
(c) 3√31
(d) 3√7
Ans: d
Sol:
Q2: For some positive and distinct real numbers x,y and z, if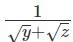 
is the arithmetic mean of 
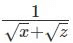and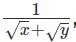 
then the relationship which will always hold true, is
(a) √x, √y and √z are in arithmetic progression
(b) √x, √z and √y are in arithmetic progression
(c) y, x and z are in arithmetic progression
(d) x, y and z are in arithmetic progression
Ans: c
Sol:
x is the Arithmetic Mean of z & y, therefore, z, x, y form an A.P.
It goes without saying that y, x, z also forms an A.P.
The document CAT Previous Year Questions - Square Root and Cube Root | Quantitative Aptitude (Quant) is a part of the CAT Course Quantitative Aptitude (Quant).
All you need of CAT at this link: CAT
|
184 videos|237 docs|103 tests
|
FAQs on CAT Previous Year Questions - Square Root and Cube Root - Quantitative Aptitude (Quant)
| 1. What are square roots and cube roots, and how are they calculated? |  |
Ans. Square roots are values that, when multiplied by themselves, give the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. Cube roots are similar but involve multiplying a number by itself twice. For instance, the cube root of 27 is 3 because 3 x 3 x 3 = 27. To calculate square roots, you can use methods like prime factorization or estimation, while cube roots can be calculated by finding the number that, when cubed, equals the target number.
| 2. Why are square roots and cube roots important in competitive exams like the CAT? | |
Ans. Square roots and cube roots are fundamental concepts in mathematics that frequently appear in competitive exams like the CAT. They are essential for solving problems related to algebra, geometry, and number theory. Understanding these concepts helps in tackling quantitative aptitude questions efficiently, as they often require quick calculations and simplifications.
| 3. How can I practice square root and cube root questions for the CAT exam? | |
Ans. To practice square root and cube root questions for the CAT exam, you can use various resources such as online mock tests, practice books, and previous year question papers. Websites and apps that focus on quantitative reasoning often have sections dedicated to these topics. Additionally, joining study groups or forums can help you exchange tips and solve problems collaboratively.
| 4. What are some common tricks to solve square root and cube root problems quickly? | |
Ans. Common tricks include memorizing squares and cubes of integers up to a certain number (e.g., 1-20), which can help you recognize patterns quickly. For square roots, knowing that √a * √b = √(ab) can simplify calculations. For cube roots, understanding that (a*b)³ = a³ * b³ can also aid in finding answers faster. Estimation techniques, like rounding numbers to the nearest perfect square or cube, can further speed up problem-solving.
| 5. Are there any formulas related to square roots and cube roots that I should know for the CAT? | |
Ans. Yes, there are several important formulas. For square roots, the formula √(a*b) = √a * √b is useful, as is the property that √(a²) = a. For cube roots, the formula (a*b)³ = a³ * b³ is important to remember. Understanding these properties can help simplify complex problems and enhance calculation speed during the exam.
About this Document
Sep 26, 2025
Last updated
Related Exams
Document Description: CAT Previous Year Questions - Square Root and Cube Root for CAT 2025 is part of Quantitative Aptitude (Quant) preparation.
The notes and questions for CAT Previous Year Questions - Square Root and Cube Root have been prepared according to the CAT exam syllabus. Information about CAT Previous Year Questions - Square Root and Cube Root covers topics
like 2024, 2023 and CAT Previous Year Questions - Square Root and Cube Root Example, for CAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for CAT Previous Year Questions - Square Root and Cube Root.
Introduction of CAT Previous Year Questions - Square Root and Cube Root in English is available as part of our Quantitative Aptitude (Quant)
for CAT & CAT Previous Year Questions - Square Root and Cube Root in Hindi for Quantitative Aptitude (Quant) course.
Download more important topics related with notes, lectures and mock test series for CAT
Exam by signing up for free. CAT: CAT Previous Year Questions - Square Root and Cube Root | Quantitative Aptitude (Quant)
Description
Full syllabus notes, lecture & questions for CAT Previous Year Questions - Square Root and Cube Root | Quantitative Aptitude (Quant) - CAT | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude (Quant) | Best notes, free PDF download
Information about CAT Previous Year Questions - Square Root and Cube Root
In this doc you can find the meaning of CAT Previous Year Questions - Square Root and Cube Root defined & explained in the simplest way possible. Besides explaining types of
CAT Previous Year Questions - Square Root and Cube Root theory, EduRev gives you an ample number of questions to practice CAT Previous Year Questions - Square Root and Cube Root tests, examples and also practice CAT
tests
Related Searches
CAT Previous Year Questions - Square Root and Cube Root | Quantitative Aptitude (Quant)
,video lectures
,ppt
,practice quizzes
,shortcuts and tricks
,CAT Previous Year Questions - Square Root and Cube Root | Quantitative Aptitude (Quant)
,Summary
,Previous Year Questions with Solutions
,Objective type Questions
,study material
,MCQs
,Free
,past year papers
,Exam
,Semester Notes
,Viva Questions
,CAT Previous Year Questions - Square Root and Cube Root | Quantitative Aptitude (Quant)
,mock tests for examination
,Extra Questions
,Important questions
,Sample Paper
;
Additional Information about CAT Previous Year Questions - Square Root and Cube Root for CAT Preparation
CAT Previous Year Questions - Square Root and Cube Root Free PDF Download
The CAT Previous Year Questions - Square Root and Cube Root is an invaluable resource that delves deep into the core of the CAT exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the CAT Previous Year Questions - Square Root and Cube Root now and kickstart your journey towards success in the CAT exam.
Importance of CAT Previous Year Questions - Square Root and Cube Root
The importance of CAT Previous Year Questions - Square Root and Cube Root cannot be overstated, especially for CAT aspirants.
This document holds the key to success in the CAT exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
CAT Previous Year Questions - Square Root and Cube Root Notes
CAT Previous Year Questions - Square Root and Cube Root Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to CAT Previous Year Questions - Square Root and Cube Root.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, CAT Previous Year Questions - Square Root and Cube Root Notes on EduRev are your ultimate resource for success.
CAT Previous Year Questions - Square Root and Cube Root CAT
The "CAT Previous Year Questions - Square Root and Cube Root CAT Questions" guide is a valuable resource for all aspiring students preparing for the
CAT exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study CAT Previous Year Questions - Square Root and Cube Root on the App
Students of CAT can study CAT Previous Year Questions - Square Root and Cube Root alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the CAT Previous Year Questions - Square Root and Cube Root,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of CAT Previous Year Questions - Square Root and Cube Root is prepared as per the latest CAT syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup