CONGRUENCE OF TRIANGLES - Class 7 PDF Download
Ref: https://edurev.in/question/744472/draw-two-triangle-to-show-that-the-AAA-is-not-congruent-conditions-with-the-help-of-figure-please-
Congruence is the term used to define an object and its mirror image. Two objects or shapes are said to be congruent if they superimpose on each other. Their shape and dimensions are same. In case of geometric figures, line segments with same length are congruent and angles with same measure are congruent. Let’s see criteria of congruence of triangles with proof.
CONGRUENCE OF TRIANGLES
A polygon made of three line segments forming three angles is known as Triangle.
Two triangles are said to be congruent if their sides have same length and angles have same measure. Thus two triangles can be superimposed side to side and angle to angle.
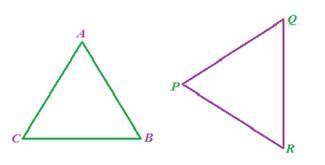
In the above figure, D ABC and D PQR are congruent triangles. This means,
Vertices: A and P, B and Q, and C and R are same.
Sides: AB=PQ, QR= BC and AC=PR;
Angles: Ð A = Ð P, ÐB = ÐQ and Ð C= Ð R.
Congruent triangles are triangles having corresponding sides and angles to be equal. Congruence is denoted by the symbol ≅. They have same area and same perimeter.
Congruence of triangles can be predicted without actually measuring the sides and angles. Different rules of congruence of triangles are as follows:
- SSS (Side-Side-Side):
If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule.

In above given figure, AB= PQ, QR= BC and AC=PR, hence D ABC ≅ D PQR.
- SAS (Side-Angle-Side):
If any two sides and angle included between the sides of one triangle are equivalent to the corresponding two sides and the angle between the sides of the second triangle, then the two triangles are said to be congruent by SAS rule.
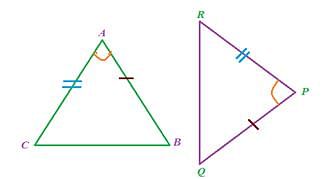
In above given figure, sides AB= PQ, AC=PR and angle between AC and AB equal to angle between PR and PQ i.e. Ð A = Ð P, hence D ABC ≅ D PQR.
- ASA (Angle-Side- Angle)
If any two angles and side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.
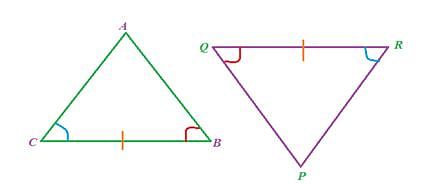
In above given figure, Ð B = Ð Q, Ð C = Ð R and sides between Ð B and ÐC , Ð Q and Ð R are equal to each other i.e. BC= QR, hence D ABC ≅ D PQR.
- RHS (Right angle- Hypotenuse-Side)
If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, the right triangles are said to be congruent by RHS rule.
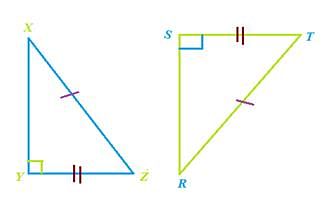
In above figure, hypotenuse XZ = RT and side YZ=ST, hence triangle XYZ ≅ triangle RST.
| Let’s Work Out: Example: In the following figure, AB = BC and AD = CD. Show that BD bisects AC at right angles. 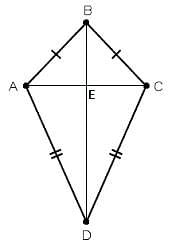 Solution: We are required to prove ∠BEA = ∠BEC = 90° and AE = EC. Consider ∆ABD and ∆CBD, AB = BC (Given) AD = CD (Given) BD = BD (Common) Therefore, ∆ABD ≅ ∆CBD (By SSS congruency) ∠ABD = ∠CBD (CPCTC) Now, consider ∆ABE and ∆CBE, AB = BC (Given) ∠ABD = ∠CBD (Proved above) BE = BE (Common) Therefore, ∆ABE≅ ∆CBE (By SAS congruency) ∠BEA = ∠BEC (CPCTC) And ∠BEA +∠BEC = 180° (Linear pair) 2∠BEA = 180° (∠BEA = ∠BEC) ∠BEA = 180°/2 = 90° = ∠BEC AE = EC (CPCTC) Hence, BD is perpendicular bisector of AC. |
FAQs on CONGRUENCE OF TRIANGLES - Class 7
| 1. What are congruent triangles? |  |
| 2. How do you prove that two triangles are congruent? |  |
| 3. Can two triangles be congruent if only their corresponding angles are equal? |  |
| 4. Are all equilateral triangles congruent to each other? |  |
| 5. Is it possible for two right-angled triangles to be congruent without having equal hypotenuses? |  |

|
Explore Courses for Class 7 exam
|

|
















