Calculus | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Q1: The expression for computing the effective interest rate (ieff) using continuous compounding for a nominal interest rate of 5% is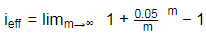
The effective interest rate (in percentage) is ______(rounded off to 2 decimal places). [2024 , Set-ll]
Ans: 5.11 to 5.15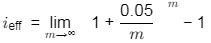
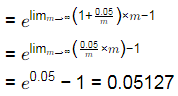
Q2: Three vectors 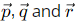 are given as
are given as
Which of the following is/are CORRECT? [2024 , Set-ll]
(a) 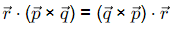
(b)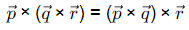
(c)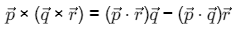
(d) 
Ans: (a, c, d)
(A) 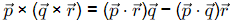
(This is always true for any three given vectors)
(B) We know that 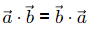 is always true but
is always true but 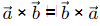 because
because 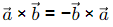
This can be true only when 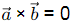
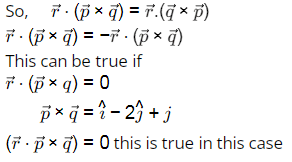
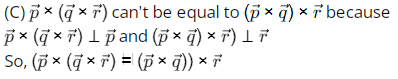
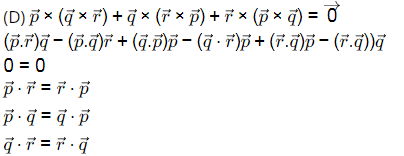
(Hence proved)
Q3: The function f(x) = x3 − 27x + 4 , 1 ≤ x ≤ 6 has [2024 , Set-ll]
(a) Inflection point
(b) Saddle point
(c) Minima point
(d) Maxima point
Ans:(c)
3x2 - 27 = 0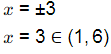
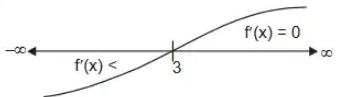
So at x = 3 function has point at local minima.
Q4: The second derivative of a function F is computed using the fourth-order Central Divided Difference method with a step length h.
The CORRECT expression for the second derivative is [2024 , Set-ll]
(a) 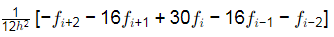
(b) 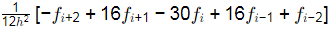
(c) 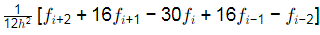
(d) 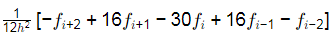
Ans: (d)
The second derivative of a function of using fourth order central divided difference method is given by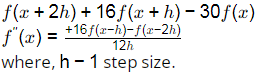
Q5: A vector field and a scalar field r are given by
and a scalar field r are given by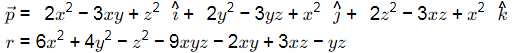
Consider the statement P and Q :
P : Curl of the gradient of the scalar field r is a null vector.
Q : Divergence of curl of the vector field 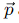 is zero.
is zero.
Which one of the following options is CORRECT? [2024 , Set-l]
(a) P is TRUE and Q FALSE
(b) P is FALSE and Q is TRUE
(c) Both P and Q are TRUE
(d) Both P and Q are FALSE
Ans: (c)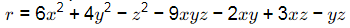
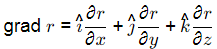
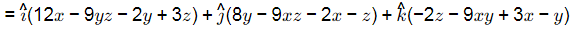
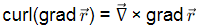
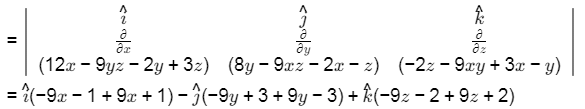
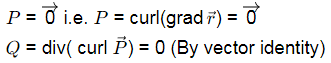
Hence both are true. Hence option (D).
Q6: The smallest positive root of the equation x5 − 5x4 −10x3 + 50x2 + 9x − 45 = 0 lies in the range [2024 , Set-l]
(a) 10 ≤ x ≤ 100
(b) 6 ≤ x ≤ 8
(c) 2 < x ≤ 4
(d) 0 < x ≤ 2
Ans: (d)
Taking option (A) 0 ≤ x ≤ 2
f(0) = 0 − 45 < 0
f(2) = 25 − 5(2)4 − 10(2)3 + 50 (2)2 + 9 × 2 − 45
= + 45 > 0 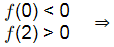
hence there will be one root in this interval which will be smallest root as per the given option.
Q7: Two vectors [2 1 0 3]τand [1 0 1 2]τbelong to the null space of a 4 × 4 matrix of rank 2. Which one of the following vectors also belongs to the null space? [2023, Set-ll]
(a) [11−11]τ
(b) [2 0 1 2]τ
(c) [0 − 2 1 − 1]τ
(d) [3 1 1 2]τ
Ans:(a)
Given matrix is 4 × 4 4×4 and rank of matrix is 2.
Therefore, rank of matrix = No. of variables Thus, there two linearly dependent vectors & two linearly independent vectors are present.
X1 = [2 1 0 3]τ
X2 = [1 0 1 2]τ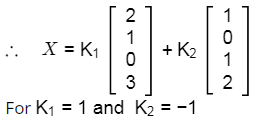
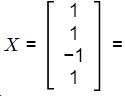 τ
τ
Q8: Let ϕ be a scalar field, and u be a vector field. Which of the following identities is true for div (ϕu) ? [2023, Set-II]
(a) div(ϕu) = ϕ div(u) + u ⋅ grad(ϕ)
(b) div(ϕu) = ϕ div(u) + u × grad(ϕ)
(c) div (ϕu) = ϕ grad(u) + u⋅grad(ϕ)
(d) div(ϕu) = ϕ grad(u) + u × grad(ϕ)
Ans: (a)
div(ϕu) = ϕdiv(μ) + ugrad(ϕ)
Q9: For the function f (x) = ex∣sin x∣ ; 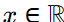 , which of the following statements is/are TRUE? (a) The function is continuous at all x [2023, Set-I]
, which of the following statements is/are TRUE? (a) The function is continuous at all x [2023, Set-I]
(b) The function is differentiable at all x
(c) The function is periodic
(d) The function is bounded
Ans: (a)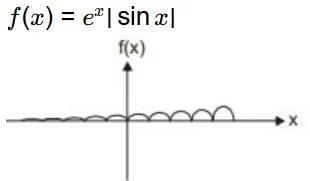
From above graph its clear that for every 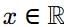
limh+0 f(x − h) = limh+0 f(x + h) = f(x)
So, function is always continuous but in the graph there are corner points so function is not differentiable.
Q10: The following function is defined over the interval [−L, L]:
f(x) = px4 + qx5
If it is expressed as a Fourier series,
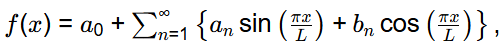
which options amongst the following are true?
(a) an, n = 1,2,...,∞ depends on p
(b) an, n = 1,2,...,∞ depends on q
(c) bn, n = 1,2,...,∞ depends on p
(d) bn, n = 1,2,...,∞ depends on q
Ans: (b, c)
f(x) = px4 + qx
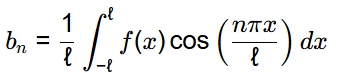
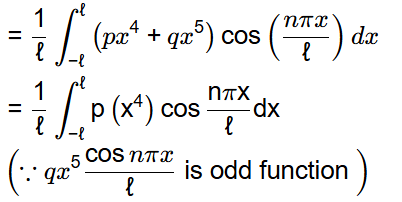
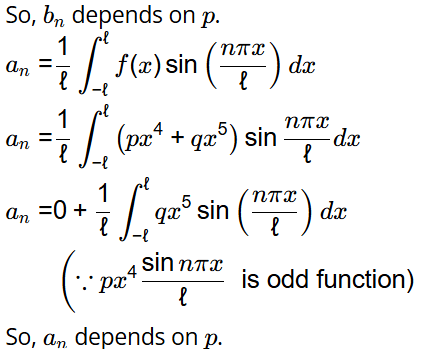
Q11: What is curl of the vector field 2x2yi + 5z2j - 4yzk? [2019 : 1 Mark, Set-ll]
(a)-14zi-2x2k
(b)6zi + 4x2j - 2x2k
(c)- 14zi + 6yj + 2x2k
(d)6zi - 8xyj + 2x2yk
Answer: (a)
Solution:
Question 12: Euclidean norm (length) of the vector [4 -2 -6]r is [2019 : 1 Mark, Set-ll]
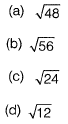
Answer: (b)
Solution:
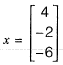
Euclidean norm length
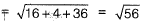
Question 13: The following inequality is true for all x close to 0.
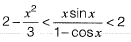
What is tha value of 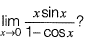 [2019 : 1 Mark, Set-ll]
[2019 : 1 Mark, Set-ll]
(a) 1
(b) 0
(c) 1/2
(d) 2
Answer: (d)
Solution:
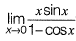
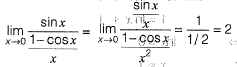
Question 14: Consider the functions: x = y In φ and y = φ In y. which one of the following the correct expression for 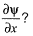 [2019 : 2 Mark, Set-l]
[2019 : 2 Mark, Set-l]
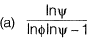
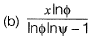
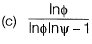
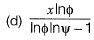
Answer: (a)
Solution:
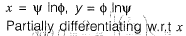
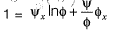 ......(i)
......(i)
Question 15: Which one of the following is NOT a correct statement? [2019 : 2 Marks, Set-I]
(a) The function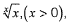 has the global minima at x = e
has the global minima at x = e
(b) The function 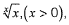 has the global maxima at x = a
has the global maxima at x = a
(c) The function x3 has neither global minima nor global maxima
(d) The function |x| has the global minima at x = 0
Answer: (a)
Solution:Let y = x1/x
log y = logx/x
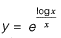
y maximum (or) minimum when,
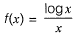 is maximum (or) minimum
is maximum (or) minimum
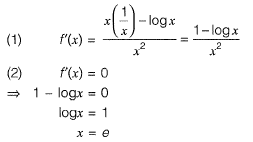
Question 16: For a small value of h, the Taylor series expansion for f(x +h) is [2019 : 1 Mark, Set-I]
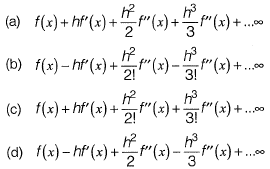
Answer:(c)
Solution:Taylor series of f (x + h) at x.
f(x + h) = f(x) + (x + h - x)
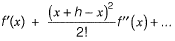
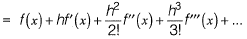
Question 17: Which of the following is correct? [2019 : 1 Mark, Set-I]
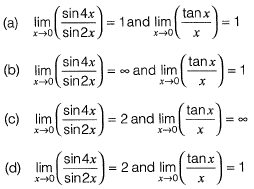
Answer: (d)
Solution:
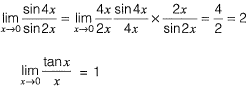
Question 18: The value (up to two decimal places) of a line 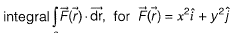 along C which is a straight line joining (0, 0) to (1, 1) is _____. [2018 : 2 Marks, Set-II]
along C which is a straight line joining (0, 0) to (1, 1) is _____. [2018 : 2 Marks, Set-II]
Solution:
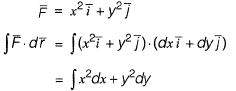
(0, 0) to (1, 1) line is y = x
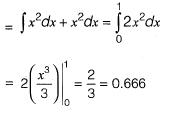
Question 19: The value of the integral 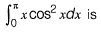 [2018 : 2 Marks, Set-I]
[2018 : 2 Marks, Set-I]
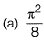
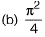
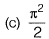
(d) ∏2
Answer: (b)
Solution:
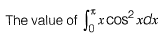
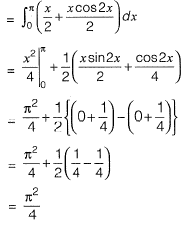
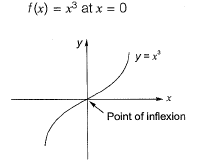
Question 20: At the point x = 0, the function f(x) = x3 has [2018 : 1 Marks, Set-I]
(a) local maximum
(b) local minimum
(c) both local maximum and minimum
(d) neither local maximum nor local minimum
Answer:(d)
Solution:
Question 21: Consider the following definite integral:
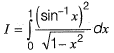
The value of the integral is [2017 : 2 Marks, Set-II]
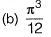
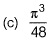
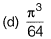
Answer:(a)
Solution:
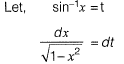
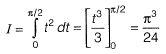
Question 22: The tangent to the curve represented by y = x In x is required to have 45° inclination with the x-axis. The coordinates of the tangent point would be [2017 : 2 Marks, Set-II]
(a) (1,0)
(b) (0,1)
(c) (1,1)
(d) 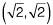
Answer: (a)
Solution: 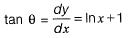
tan 45° = In x + 1
1 = lnx + 1
⇒ Inx = 0
∴ x = 1
Putting x = 1 in the eq. of curve, we get y = 0.
Question 23: The divergence of the vector field V = x2i + 2y3j + z4k at x = 1, y = 2, z = 3 is _________. [2017 : 1 Mark, Set-II]
Solution: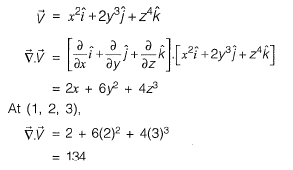
Question 24: Let w= f(x, y), where x and yare functions of t. Then, according to the chain rule dw/dt [2017 : 1 Mark, Set-II]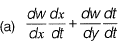

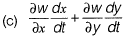
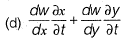
Answer: (c)
Solution:W = f(x, y)
By Chain rule,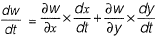
Question 25: Let x be a continuous variable defined over the interval (-∞, ∞), and 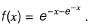 The integral
The integral 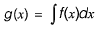 is equal to [2017 : 1 Mark, Set-I]
is equal to [2017 : 1 Mark, Set-I]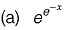
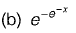
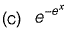
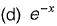
Answer:(b)
Solution: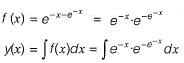
Let e-x = t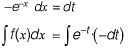
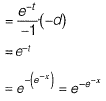
Question 26: [2017 : 1 Mark, Set-I]
[2017 : 1 Mark, Set-I]
Solution: 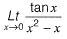 (Applying L'Hospital rule)
(Applying L'Hospital rule)
= 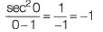
Question 27: The quadratic approximation of
f(x) = x3 - 3x2 - 5 a the point x = 0 is [2016 : 2 Marks, Set-II]
(a) 3x2 - 6x - 5
(b) -3x2 - 5
(c) -3x2 + 6x - 5
(d) 3x2 - 5
Answer:(b)
Solution:The quadratic approximation of f{x) at the point x = 0 is,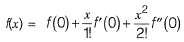
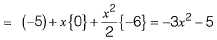
Question 28: The area between the parabola x2 = 8y and the straight line y = 8 is______. [2016 : 2 Marks, Set-II]
Solution:Parabola is x2 = 8y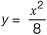 and straight is y = 0
and straight is y = 0
At the point of intersection, we have,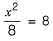
⇒ 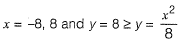
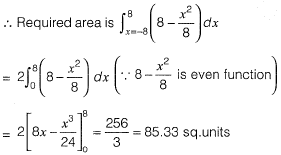
Question 29: The angle of intersection of the curves x2 = 4y and y2 = 4x at point (0, 0) is [2016 : 2 Marks, Set-II]
(a) 0°
(b) 30°
(c) 45°
(d) 90°
Answer:(d)
Solution:Given curve,
x2 = 4y .......(i)
and y2 = 4x ........(ii)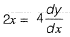
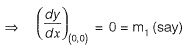


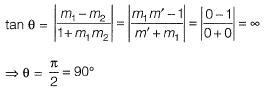
Question 30: The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is
(a) 59/6
(b) 9/2
(c) 10/3
(d) 7/6
Answer:(b)
Solution:At the point of intersection of the curves,
y = x2 + 1 and x + y = 3 i.e., y = 3 - x , we have,
x2 + 1 - 3 - x ⇒ x2 + x - 2 = 0
⇒ x = -2, 1 and 3 - x > x2 + 1
Question 31: The value of  [2016 : 2 Marks, Set-I]
[2016 : 2 Marks, Set-I]
(a) π/2
(b) π
(c) 3π/2
(d) 1
Answer:(b)
Solution:

(Using "division by x")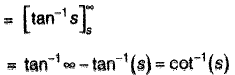
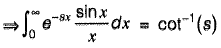
(Using definition of Laplace transform)
Put s - 0, we get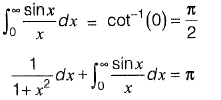
Question 32: What is the value of 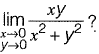 [2016 : 1 Mark, Set-II]
[2016 : 1 Mark, Set-II]
(a) 1
(b) -1
(c) 0
(d) Limit does not exit
Answer: (d)
Solution: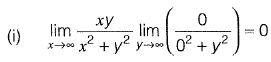
(i.e., put x = 0 and then y = 0)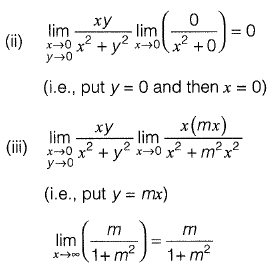
which depends on m.
Question 33: The optimum value of the function f(x) = x2 - 4x + 2 is [2016 : 1 Mark, Set-II]
(a) 2 (maximum)
(b) 2 (minimum)
(c) -2 (maximum)
(d) -2 (minimum)
Answer:(d)
Solution:
f'(x) = 0
⇒ 2x — 4 = 0
⇒x = 2 (stationary point)
f"(x) = 2 > 0
⇒ f(x) is minimum at x = ?
i.e., (2)2 - 4(2) + 2 = -2
∴ The optimum value of f(x) is -2 (minimum)
Question 34: While minimizing the function f(x), necessary and sufficient conditions for a point x0 to be a minima are [2015 : 1 Mark, Set-II]
(a) f' (x0) > 0 and f" (x0) = 0
(b) f'(x0)< 0 an d f"(x0) = 0
(c) f' (x0) = 0 and f" (x0) < 0
(d) f' (x0) = 0 and f" (x0) > 0
Answer: (d)
Solution: f(x) has a local minimum at x = x0
if f'(x0) = 0 and f''(x0) > 0
Question 35: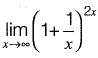 is equal to [2015 : 1 Mark, Set-II]
is equal to [2015 : 1 Mark, Set-II]
(a) e-2
(b) e
(c) 1
(d) e2
Answer:(d)
Solution: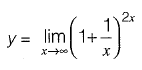
⇒ 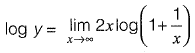
Which is in the form of 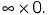
To convert this into 0/0 form, we rewrite as,
⇒ 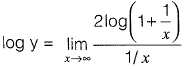
Now it is in 0/0 form.
Using L’Hospital’s rule,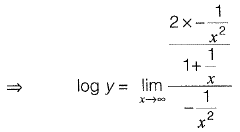
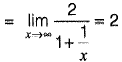
∴ y = e2
Question 36: The directional derivative of the field u(x, y, z) = x2 - 3yz in the direction of the vector 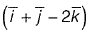 at point (2, - 1, 4) is _________. [2015 : 2 Marks, Set-I]
at point (2, - 1, 4) is _________. [2015 : 2 Marks, Set-I]
Solution: 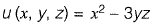

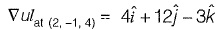
Directional derivative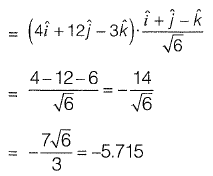
Question 37: The expression 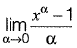 is equal to [2014 : 2 Marks, Set-II]
is equal to [2014 : 2 Marks, Set-II]
(a) ln x
(b) 0
(c) x ln x
(d) ∞
Answer:(a)
Solution: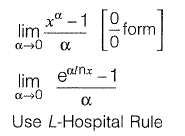
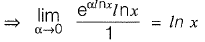
Question 38: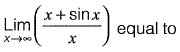 [2014 : 1 Marks, Set-I]
[2014 : 1 Marks, Set-I]
(a) -∞
(b) 0
(c) 1
(d) ∞
Answer: (c)
Solution: Put 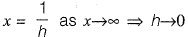

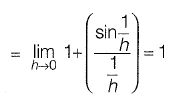
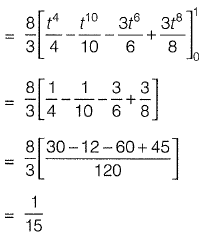
Question 39: The value of 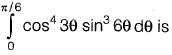 [2013 : 2 Marks]
[2013 : 2 Marks]
(a) 0
(b) 1/15
(c) 1
(d) 8/3
Answer:(b)
Solution: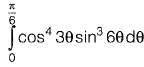

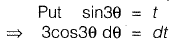
⇒ 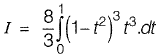
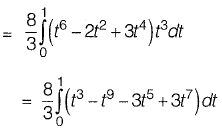
Alternative Method: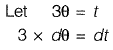
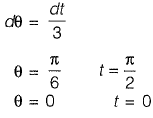
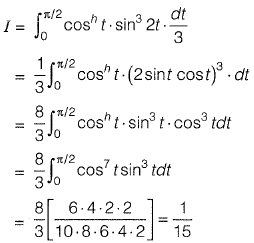
Question 40: For the parallelogram OPQR shown in the sketch, 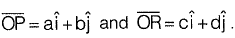 The area of the parallelogram is [2011 : 2 Marks]
The area of the parallelogram is [2011 : 2 Marks]
(a) ad - bc
(b) ac + bd
(c) ad + bc
(d) ab - cd
Answer:(a)
Solution: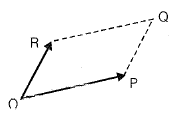
The area of parallelogram OPQR in figure shown above, is the magnitude of the vector product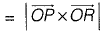
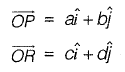

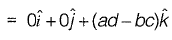
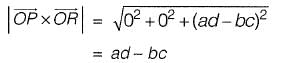
FAQs on Calculus - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What is the Fundamental Theorem of Calculus and why is it important? |  |
| 2. How do you find the derivative of a function? |  |
| 3. What are some common applications of integrals in real life? |  |
| 4. What is the difference between definite and indefinite integrals? |  |
| 5. How do you apply integration techniques like substitution and integration by parts? |  |





















