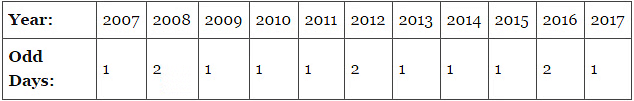Calendars: Solved Examples- 1 | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
Question 1: If 15 March 1816 was Friday, what day of the week would 15th April 1916 be?
A. Monday
B. Wednesday
C. Thursday
D. Saturday
Ans: D
We are given that 15th March 1816 was a Friday.
Now we know that 100 years have 5 odd days. So till 15th March 1916, we will be having 5 odd days. So if we move from 15th March 1816 to 15th March 1916, we will encounter 5 odd days.
Now from 15th March 1916 to 15th April 1916 there would be 3 odd days.
So total number of odd days = 5+3 =8
8 mod 7 = 1
So 15th April 1916 would be Friday + 1= Saturday
Question 2: Today is Monday. After 61 days, it will be:
A. Wednesday
B. Saturday
C. Tuesday
D. Thursday
Ans: B
Each day of the week repeats every 7 days.
7 × 9 = 63 days ⇒ back to Monday.
61 days is 2 days fewer than 63, so 2 days before Monday is Saturday.
∴ After 61 days, it will be Saturday.
Question 3: If 28th August 1946 was a Wednesday, what day of the week was 31 August 1961?
A. Tuesday
B. Thursday
C. Monday
D. Wednesday
Ans: B
It is given that 28th August 1946 was Wednesday. From 28th August 1946 to 28th August 1961, we have 4 leap years and 11 normal years. So the number of odd days would be
11x1 + 4x2 = 19
Now the date which is asked is 31 Aug 1961. So if we move from 28th August to 31st August, we will have 3 more odd days.
So total number of odd days = 5 + 3 = 8
Now 8 mod 7 = 1 .
So 31st August 1961 would be Wednesday + 1 = Thursday.
Question 4: If 09/12/2001(DD/MM/YYYY) happens to be Sunday, then 09/12/1971 would have been
A. Wednesday
B. Tuesday
C. Saturday
D. Thursday
Ans: D
30 years. The number of leap years is 8 (1972,1976,1980,1984,1988,1992,1996,2000).
So, the total number of days = 22x365 + 8x366 = 10958
10958 mod 7 = 3
Since 9/12/2001 is a Sunday,
9/12/1971 should be a Thursday.
Question 5: In 2016, Mohan celebrated his birthday on Friday. Which will be the first year after 2016 when Mohan will celebrate his birthday on a Wednesday? (He was not born in January or February)
A. 2021
B. 2023
C. 2020
D. 2025
Ans: C
Since it has been mentioned that Mohan was not born in February, so he can’t be born on 29th Feb. Hence He will celebrate his next birthday on a Wednesday in the year for which the sum of the odd days becomes 5 or a multiple of 5.
By his birthday in 2017, there will be 1 odd day.
By his birthday in 2018, there will be 2 odd days.
By his birthday in 2019, there will be 3 odd days.
By his birthday in 2020, there will be 5 odd days, as 2020 is a leap year.
So in 2020 He will celebrate his birthday on Wednesday.
Question 6: What day of the week does May 28, 2006, fall on
A. Saturday
B. Monday
C. Sunday
D. Thursday
Ans: C
28th May 2006 = (2005 years + period from 1-Jan-2006 to 28-May-2006)
We know that number of odd days in 400 years = 0
Hence the number of odd days in 2000 years = 0 (Since 2000 is a perfect multiple of 400)
Number of odd days in the period 2001-2005
= 4 normal years + 1 leap year
= 4 x 1 + 1 x 2 = 6
Days from 1-Jan-2006 to 28-May-2006 = 31 (Jan) + 28 (Feb) + 31 (Mar) + 30 (Apr) + 28(may)
= 148
148 days = 21 weeks + 1 day = 1 odd day
Total number of odd days = (0 + 6 + 1) = 7 odd days = 0 odd day
0 odd day = Sunday
Hence May 28 2006 is Sunday.
Question 7: What will be the day of the week on 15th August, 2010?
A. Thursday
B. Sunday
C. Monday
D. Saturday
Ans: B
15th Aug 2010 = (2009 years + period from 1-Jan-2010 to 15-Aug-2010)
We know that number of odd days in 400 years = 0
Hence the number of odd days in 2000 years = 0 (Since 2000 is a perfect multiple of 400)
Number of odd days in the period 2001-2009
= 7 normal years + 2 leap year
= 7 x 1 + 2 x 2 = 11 = (11 - 7x1) odd day = 4 odd day
Days from 1-Jan-2010 to 15-Aug-2010
= 31 (Jan) + 28 (Feb) + 31 (Mar) + 30 (Apr) + 31(may) + 30(Jun) + 31(Jul) + 15(Aug)
= 227
227 days = 32 weeks + 3 day = 3 odd day
Total number of odd days = (0 + 4 + 3) = 7 odd days = 0 odd day
0 odd day = Sunday
Hence 15th August, 2010 is Sunday.
Question 8: Today is Tuesday. After 52 days, it will be
A. Thursday
B. Friday
C. Monday
D. Saturday
Ans: B
Each day of the week repeats every 7 days.
7 × 7 = 49 days ⇒ back to Tuesday.
52 days is 3 days more than 49, so 3 days after Tuesday is Friday.
∴ After 52 days, it will be Friday,
Question 9: On what dates of April, 2001 did Wednesday fall?
A. 2nd, 9th, 16th, 23rd
B. 4th, 11th, 18th, 25th
C. 3rd, 10th, 17th, 24th
D. 1st, 8th, 15th, 22nd, 29th
Ans: B
We need to find out the day of 01-Apr-2001
01-Apr-2001 = (2000 years + period from 1-Jan-2001 to 01-Apr-2001)
We know that number of odd days in 400 years = 0
Hence the number of odd days in 2000 years = 0 (Since 2000 is a perfect multiple of 400)
Days from 1-Jan-2001 to 01-Apr-2001 = 31 (Jan) + 28 (Feb) + 31 (Mar) + 1(Apr) = 91
91 days = 13 weeks = 0 odd day
Total number of odd days = (0 + 0) = 0 odd days
0 odd day = Sunday. Hence 01-Apr-2001 is Sunday.
Hence theWednesday of Apr 2011 comes in 04th ,11th, 18th and 25th
Question 10: How many days are there in x weeks x days
A. 14x
B. 8x
C. 7x2
D. 7
Ans: B
x weeks x days =(7×x)+x
=7x+x
=8x
Question 11: The calendar for the year 2007 will be the same for the year
A. 2017
B. 2018
C. 2014
D. 2016
Ans: B
For a year to have the same calendar with 2007 ,the total odd days from 2007 should be 0.
Year : 2007 2008 2009 2010 2011 2012 2013 20142015 2016 2017
Odd day: 1 2 1 1 1 2 1 1 1 2 1
Sum = 14 odd days ≡ 0 odd days.Therefore, Calendar for the year 2018 will be the same as for the year 2007.
Question 12: Which of the following is not a leap year?
A. 1200
B. 800
C. 700
D. 2000
Ans: C
Remember the leap year rule (Given in the formulas)
1. Every year divisible by 4 is a leap year, if it is not a century.
2. Every 4th century is a leap year, but no other century is a leap year.
800,1200 and 2000 comes in the category of 4th century (such as 400,800,1200,1600,2000 etc).
Hence 800,1200 and 2000 are leap years
700 is not a 4th century, but it is a century. Hence it is not a leap year
Question 13: 01-Jan-2007 was Monday. What day of the week lies on 01-Jan-2008?
A. Wednesday
B. Sunday
C. Friday
D. Tuesday
Ans: D
Given that January 1, 2007 was Monday.
Odd days in 2007 = 1 (we have taken the complete year 2007 because we need to find out the odd days from 01-Jan-2007 to 31-Dec-2007, that is the whole year 2007)
Hence January 1, 2008 = (Monday + 1 Odd day) = Tuesday
Question 14: 8th Dec 2007 was Saturday, what day of the week was it on 8th Dec, 2006?
A. Sunday
B. Tuesday
C. Friday
D. Tuesday
Ans: C
Given that 8th Dec 2007 was Saturday
Number of days from 8th Dec, 2006 to 7th Dec 2007 = 365 days
365 days = 1 odd day
Hence 8th Dec 2006 was = (Saturday - 1 odd day) = Friday
Question 15: On 8th Feb, 2005 it was Tuesday. What was the day of the week on 8th Feb, 2004?
A. Sunday
B. Friday
C. Saturday
D. Monday
Ans: A
Given that 8th Feb, 2005 was Tuesday
Number of days from 8th Feb, 2004 to 7th Feb, 2005 = 366
(Since Feb 2004 has 29 days as it is a leap year 366 days = 2 odd days)
Hence 8th Feb, 2004 = (Tuesday - 2 odd days) = Sunday
|
87 videos|172 docs|99 tests
|
FAQs on Calendars: Solved Examples- 1 - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are the different types of calendars used worldwide? |  |
| 2. How do leap years work in the Gregorian calendar? |  |
| 3. Why do we need a calendar? |  |
| 4. How can I convert dates between different calendars? |  |
| 5. What is the significance of the lunar calendar in various cultures? |  |