Cayley’s theorem | Algebra - Mathematics PDF Download
We have stated that on of the main objectives of group theory is to write down a complete list of non-isomorphic groups. At first, such a task appears hopeless. For, as we have seen, groups pop up in some very unexpected places and, therefore, if we set out to compile a list of all non-isomorphic groups, we would hardly begin to know where to look. The following theorem of Cayley solves this dilemma.
Theorem 1: Every group is isomorphic to a subgroup of a permutation group
Proof: Let G be a group, g  G. define
G. define
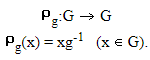
If Pg(x) = Pg(y), then xg-1 = yg-1, so that x = y. Therefore, Pg is an injection. If y  G, then Pg(yg) = yg · g-1 = y. Therefore, Pg is a surjection. Thus, since Pg is a bijection, Pg is a permutation of the elements of the set G, and Pg ∈ SG. Let us consider the mapping
G, then Pg(yg) = yg · g-1 = y. Therefore, Pg is a surjection. Thus, since Pg is a bijection, Pg is a permutation of the elements of the set G, and Pg ∈ SG. Let us consider the mapping
G → SG
defined by
g  Pg (1)
Pg (1)
Since Pgg' = x(gg')-1 = PgPg'(x), the mapping (1) is a homomorphism. But P = 1SG if and only if x · g = x for all x  G, which occurs if and only if g = 1G. Therefore, the kernel of the homomorphism (1) is 1G, and therefore the mapping (1) is an injection. Thus we have shown that G is isomorphic to a subgroup of SG.
G, which occurs if and only if g = 1G. Therefore, the kernel of the homomorphism (1) is 1G, and therefore the mapping (1) is an injection. Thus we have shown that G is isomorphic to a subgroup of SG.
What Cayley's theorem tells us is that permutation groups and their subgroups are all the groups that can exist. Unfortunately, the problem of classifying the subgroups of a permutation group is extremely complicated, even in the case of a finite permutation group. Therefore, Cayley's theorem does not allow us to easily identify a complete list of groups.
The above argument actually proves somewhat more than claimed. For if G is finite, having order n, then G is isomorphic to a subgroup of SG. Therefore we have
Corollary 2: If G has finite order n, then G is isomorphic to a subgroup of Sn.
|
181 videos|58 docs
|
FAQs on Cayley’s theorem - Algebra - Mathematics
| 1. What is Cayley's theorem in mathematics? |  |
| 2. How does Cayley's theorem relate to the study of groups? |  |
| 3. Can you provide an example of how Cayley's theorem works? |  |
| 4. What are the implications of Cayley's theorem for studying abstract groups? |  |
| 5. Are there any limitations to Cayley's theorem? |  |
















