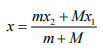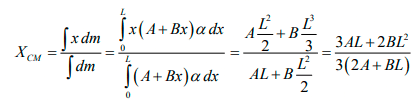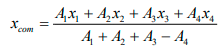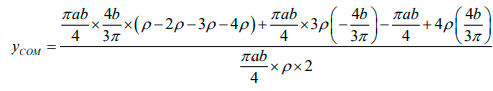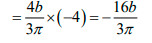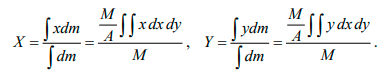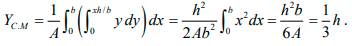Centre of Mass & Moment of Inertia: Assignment | Mechanics & General Properties of Matter - Physics PDF Download

Clear all your Physics doubts with EduRev Join for Free

Join for Free

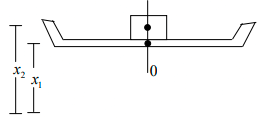
Q.1. A cubical block of ice of mass m and edge L is placed in a large tray of mass M. If the ice melts, how far does the centre of mass of the system “ice plus tray” come down? (assume base of tray is large enough so that after height of water is negligible after melting of ice.)

Consider figure. Suppose the centre of mass of the tray is a distance x₁ above the origin and that of ice at a distance x₂ above the origin. The height of the centre of mass of the ice-tray system is

                                           
When the ice melts, the water of mass m spreads on the surface of the tray. As the tray is large, the height of water is negligible. The centre of mass of the water is then on the surface of the tray and is at a distance x₂ - L/2 above the origin. The new centre of mass of the ice-tray system will be at the height

                                                    

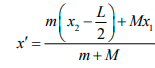
The shift in the centre of mass = x - x' = .

Q.2. Half of the rectangular plate shown in the figure is made of a material of density ρ₁ and the other half of density ρ₂. The length of the plate is L. Locate the centre of mass of the plate.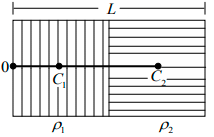

The centre of mass of each half is located at the geometrical centre of that half. Thus the left half may be replaced by a point particle of mass Kρ₁ placed at C₁ and the right half may be replaced by a point particle of mass Kρ₂ placed at C₂. This replacement is for the specific purpose of locating the combined centre of mass. Take the middle point of the left edge to be the origin. The x coordinate of C₁ is L/4 and that of C₂ is 3/4 L . Hence, the x -coordinate of the centre of mass is

                      

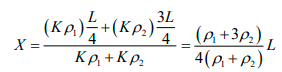
The combined centre of mass is this much to the right of the assumed origin.

Q.3. The density of a linear rod of length L varies as ρ = A + Bx , where x is the distance from the left end. Locate the centre of mass.

Let the cross-sectional area be α. The mass of an element of length dx located at a distance x away from the left end is (A + Bx) αdx. The x -coordinate of the centre of mass is given by

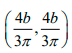
Q.4. Mass unit area of a quadrant of an ellipse are ρ,2ρ, 3ρ and 4ρ (for 1, 2, 3 and 4). One quadrant (no. 4) is cut off. Find centre of mass of remaining figure.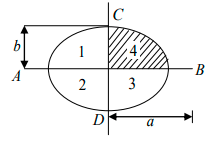

Centre of mass of a quadrant of ellipse is 

                               

Taking 0 (0,0) as reference and OB, OC , are the x and y axes.

 

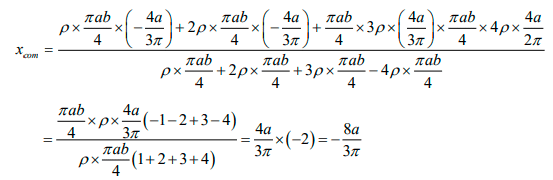
Similarly, 

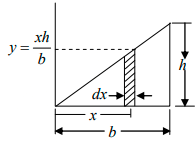
Q.5. Find the centre of mass of right angle triangular sheet of mass M, base b and height h as shown in figure.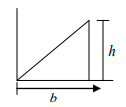

Hence the coordinates of the centre of mass are given by

                               

The double integrals may look strange, but they are easily evaluated. Consider first the double integral , where A = 1/2bh,

This integral instructs us to take each element, multiply its area by its x coordinate, and sum the results. We can do this in stages by first considering the elements in a strip parallel to the y axis. The strip runs from y = 0 to y = xh/b. Each element in the strip has the same x coordinate, and the contribution of the strip to the double integral is

Finally, we sum the contributions of all such strips x = 0 to

x = b to find

 

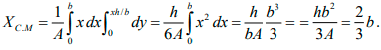
Similarly,