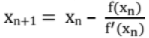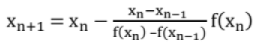Chapter - 1 Mathematics (Part - 1) | Additional Study Material for Mechanical Engineering PDF Download
Linear Algebra
1. Matrix
Definition: A system of "m n" numbers arranged along m rows and n columns.
Conventionally, single capital letter is used to denote a matrix.
Thus,
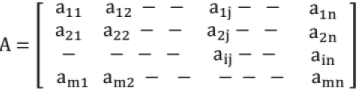
aij → ith row, jth column
1. Types of Matrices
- Row Matrix → [ 2, 7, 8,9] → single row (or row vector)
- Column Matrix
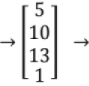 single column (or column vector)
single column (or column vector)
3. Square Matrix
- Same number of rows and columns.
- Order of Square matrix → no. of rows or columns
- Principle Diagonal (or Main diagonal or Leading diagonal): The diagonal of a square matrix (from the top left to the bottom right) is called as principal diagonal.
- Trace of the Matrix: The sum of the diagonal elements of a square matrix,
(i) tr (λA) = λ tr(A) [λ is scalar]
(ii) tr (A+B) = tr (A) + tr (B)
(iii) tr (AB) = tr (BA)
4. Rectangular Matrix
Number of rows ≠ Number of columns
5. Diagonal Matrix
A Square matrix in which all the elements except those in leading diagonal are zero.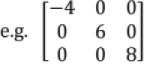
6. Unit Matrix (or Identity Matrix)
A Diagonal matrix in which all the leading diagonal elements are '1'.
e.g. 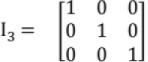
7. Null Matrix (or Zero Matrix)
A matrix is said to be Null Matrix if all the elements are zero.
e.g. 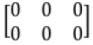
8. Symmetric and Skew Symmetric Matrices;
- Symmetric, when aij = +aji for all i and j. In other words AT = A
- Skew symmetric, when aij = - aji In other words AT = - A
Note: All the diagonal elements of skew symmetric matrix must be zero.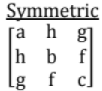
Symmetric Matrix AT = A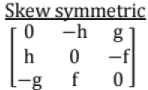
Skew Symmetric Matrix AT = - A
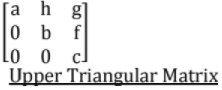
9. Triangular Matrix
- A matrix is said to be "upper triangular" if all the elements below its principal diagonal are zeros.
- A matrix is said to be "lower triangular" if all the elements above its principal diagonal are zeros.

10. Orthogonal Matrix:
If A. AT = 1, then matrix A is said to be Orthogonal matrix.
11. Singular Matrix:
If |A| = 0, then A is called a singular matrix.
12. Unitary Matrix:
If we define,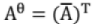 = transpose of a conjugate of matrix A Then the matrix is unitary if
= transpose of a conjugate of matrix A Then the matrix is unitary if 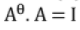
13. Hermitian Matrix:
It is a square matrix with complex entries which is equal to its own conjugate transpose.
14. Note:
In Hermitian matrix, diagonal elements → always real
15. Skew Hermitian matrix:
It is a square matrix with complex entries which is equal to the negative of conjugate transpose.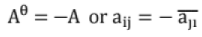
Note: In Skew-Hermitian matrix, diagonal elements -> either zero or Pure Imaginary
16. Idempotent Matrix
If A2 = A, then the matrix A is called idempotent matrix.
17. Multiplication of Matrix by a Scalar:
Every element of the matrix gets multiplied by that scalar.
Multiplication of Matrices:
Two matrices can be multiplied only when number of columns of the first matrix is equal to the number of rows of the second matrix. Multiplication of (m x n) and (n x p) matrices results in matrix of (m x p)dimension 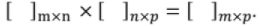
18. Determinant:
An nth order determinant is an expression associated with n x n square matrix.
If A = [aij], Element aij with ith row, jth column.
For n = 2 ; 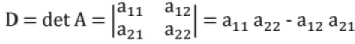
Determinant of 'order n"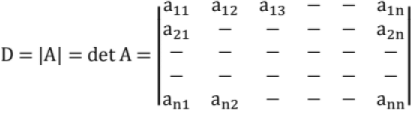
19. Minors & Co-Factors:
- The minor of an element in a determinant is the determinant obtained by deleting the row and the column which intersect that element.
- Cofactor is the minor with "proper sign". The sign is given by (-1)i+j (where the element belongs to ith row, jth column).
20. Properties of Determinants:
- A determinant remains unaltered by changing its rows into columns and columns into rows.
- If two parallel lines of a determinant are inter-changed, the determinant retains its numerical values but changes its sign. (In a general manner, a row or a column is referred as line).
- Determinant vanishes if two parallel lines are identical.
- If each element of a line be multiplied by the same factor, the whole determinant is multiplied by that factor. [Note the difference with matrix].
- If each element of a line consists of the m terms, then determinant can be expressed as sum of the m determinants.
- If each element of a line be added equimultiple of the corresponding elements of one or more parallel lines, determinant is unaffected.
e.g. by the operation, R2 → R2 + pR1 + qR3, determinant is unaffected. - Determinant of an upper triangular/ lower triangular/diagonal/scalar matrix is equal to the product of the leading diagonal elements of the matrix.
- If A & B are square matrix of the same order, then |AB|=|BA||-|A||B|.
- If A is non singular matrix, then
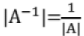 (as a result of previous).
(as a result of previous). - Determinant of a skew symmetric matrix (i.e. AT =-A) of odd order is zero.
- If A is a unitary matrix or orthogonal matrix (i.e. AT = A-1) then |A|= ±1.
- If A is a square matrix of order n, then |kA| = kn|A|.
- |1n| = 1 ( In is the identity matrix of order n).
21. Inverse of a Matrix
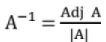
- |A| must be non-zero (i.e. A must be non-singular).
- Inverse of a matrix,, if exists, is always unique.
- If it is a 2x2 matrix
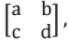 its inverse will be
its inverse will be 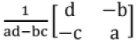
Important Points:
- 1A = A1 = A, (Here A is square matrix of the same order as that of 1)
- 0A = AO = 0 , (Here 0 is null matrix)
- If AB = 0, then it is not necessarily that A or B is null matrix. Also it doesn't mean BA = 0.
- If the product of two non-zero square matrices A & B is a zero matrix, then A & B are singular matrices.
- If A is non-singular matrix and A.B=D, then B is null matrix.
- AB ≠ BA (in general) → Commutative property does not hold
- A(BC) = (AB)C → Associative property holds
- A(B+C) = AB + AC → Distributive property holds
- AC = AD, doesn't imply C = D [even when A ≠ 0].
- If A, C, D be n x n matrix, and if rank (A) = n & AC = AD, then C=D.
- (A + B)T = AT + BT
- (AB)T = BT . AT
- (AB)-1 = B-1. A-1
- A A-1 = A -1A = 1
- (kA)T = k.AT (k is scalar, A is vector)
- (kA)-1 = k-1. A-1 (k is scalar, A is vector)
- ( A-1)T = (AT)-1
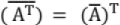 (Conjugate of a transpose of matrix = Transpose of conjugate of matrix)
(Conjugate of a transpose of matrix = Transpose of conjugate of matrix)- If a non-singular matrix A is symmetric, then A-1 is also symmetric.
- If A is a orthogonal matrix, then AT and A-1 are also orthogonal.
- If A is a square matrix of order n then
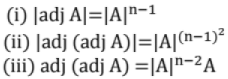
22. Elementary Transformation of a Matrix:
1. Interchange of any 2 lines
2. Multiplication of a line by a constant (e.g. k Ri)
3. Addition of constant multiplication of any line to the another line (e. g. Ri + p Rj)
Note:
- Elementary transformations don't change the rank of the matrix.
- However it changes the Eigen value of the matrix.
23. Rank of Matrix
If we select any r rows and r columns from any matrix A, deleting all other rows and columns, then the determinant formed by these r x r elements is called minor of A of order r.
Definition: A matrix is said to be of rank r when,
i) it has at least one non-zero minor of order r.
ii) Every minor of order higher than r vanishes.
Other definition: The rank is also defined as maximum number of linearly independent row vectors.
Special case; Rank of Square matrix
Rank = Number of non-zero row in upper triangular matrix using elementary transformation.
Note:
- r(A.B ) ≤ min {r (A), r (B)}
- r(A + B) ≤ r (A) + r (B)
- r(A-B) ≥ r (A) - r(B)
- The rank of a diagonal matrix is simply the number of non-zero elements in principal diagonal.
- A system of homogeneous equations such that the number of unknown variable exceeds the number of equations, necessarily has non-zero solutions.
- If A is a non-singular matrix, then all the row/column vectors are independent.
- If A is a singular matrix, then vectors of A are linearly dependent.
- r(A) = 0 iff(if and only if) A is a null matrix.
- If two matrices A and 13 have the same size and the same rank then A, B are equivalent matrices.
- Every non-singular matrix is row matrix and it is equivalent to identity matrix.
24. Solution of linear System of Equations;
For the following system of equations A X = B
Where, 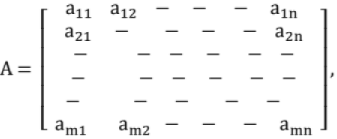
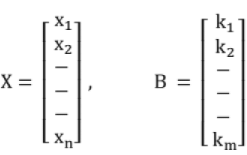
A = Coefficient Matrix, C = (A, B) = Augmented Matrix
r = rank (A), r' = rank (C), n = Number of unknown variables (x1 , x2, - - - xn)
Consistency of a System of Equations:
For Non-Homogenous Equations (A X = B)
(i) If r ≠ r', the equations are inconsistent i.e. there is no solution.
(ii) If r = r' = n, the equations are consistent and there is a unique solution.
(iii) If r = r' < n, the equations are consistent and there are infinite number of solutions.
For Homogenous Equations (A X = 0)
(i) If r = n, the equations have only a trivial zero solution ( i.e. x1 = x2 = - - - xn = 0).
(ii) If r < n, then (n-r) linearly independent solution (i.e. infinite non-trivial solutions).
Note:
Consistent means: → one or more solution (i.e. unique or infinite solution)
Inconsistent means: → No solution
Cramer's Rule
Let the following two equations be there
a11 x1 + a12 x2 = b1 ...(i)
a21 x1 + a22 x2 = b2 ...(ii)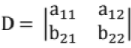
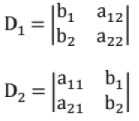
Solution using Cramer's rule: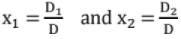
In the above method, it is assumed that
1. No of equations = No of unknowns
2. D ≠ 0
In general, for Non-Homogenous Equations
D ≠ 0 → single solution (non trivial)
D = 0 → infinite solution
For Homogenous Equations
D ≠ 0 → trivial solutions (x1 = x2 = ... xn = 0)
D = 0 → non- trivial solution (or infinite solution)
Eigen Values & Eigen Vectors
25. Characteristic Equation and Eigen Values:
Characteristic equation: |A — λ1| = 0, The roots of this equation are called the characteristic roots /latent roots / Eigen values of the matrix A.
Eigen vectors: [A - λI] X = 0
For each Eigen value λ, solving for X gives the corresponding Eigen vector.
Note: For a given Eigen value, there can be different Eigen vectors, but for same Eigen vector, there can't be different Eigen values.
Properties of Eigen values
- The sum of the Eigen values of a matrix is equal to the sum of its principal diagonal.
- The product of the Eigen values of a matrix is equal to its determinant.
- The largest Eigen values of a matrix is always greater than or equal to any of the diagonal elements of the matrix.
- If λ is an Eigen value of orthogonal matrix, then 1/ λ is also its Eigen value.
- If A is real, then its Eigen value is real or complex conjugate pair.
- Matrix A and its transpose AT has same characteristic root (Eigen values).
- The Eigen values of triangular matrix are just the diagonal elements of the matrix.
- Zero is the Eigen value of the matrix if and only if the matrix is singular.
- Eigen values of a unitary matrix or orthogonal matrix has absolute value T .
- Eigen values of Hermitian or symmetric matrix are purely real.
- Eigen values of skew Hermitian or skew symmetric matrix is zero or pure imaginary.
- |A|/λ is an Eigen value of adj A (because adj A =|A|.A-1).
- If λ is an Eigen value of the matrix then,
(i) Eigen value of A-1 is 1/λ
(ii) Eigen value of Am is Am
(iii) Eigen value of kA are kλ (k is scalar)
(iv) Eigen value of A + kI are λ + k
(v) Eigen value of (A - kl)2 are (λ - k)2
Properties of Eigen Vectors
- Eigen vector X of matrix A is not unique.
Let Xi is Eigen vector, then CXi is also Eigen vector (C = scalar constant). - If λ1, λ2, λ3 ........ λn are distinct then X1, X2........ Xn are linearly independent.
- If two or more Eigen values are equal, it may or may not be possible to get linearly independent Eigen vectors corresponding to equal roots.
- Two Eigen vectors are called orthogonal vectors if X1T•X2 = 0.
(X1, X2 are column vector)
(Note: For a single vector to be orthogonal, AT = A-1 or, A. AT = A. A-1 = 1) - Eigen vectors of a symmetric matrix corresponding to different Eigen values are orthogonal.
Cayley Hamilton Theorem: Every square matrix satisfies its own characteristic equation.
26. Vector:
- Any quantity having n components is called a vector of order n.
Linear Dependence of Vectors
If one vector can be written as linear combination of others, the vector is linearly dependent.
Linearly Independent Vectors
If no vectors can be written as a linear combination of others, then they are linearly independent.
Suppose the vectors are x1 x2 x3 x4
Its linear combination is λ1x1 + λ2x2 + λ3x3 + λ4x4 = 0 - If λ1, λ2, λ3, λ4 are not 'all zero" → they are linearly dependent.
- If all "λ" are zero → they are linearly independent.
2. Probability and Distribution
2. Probability and Distribution
1. Probability
Event: Outcome of an experiment is called event.
Mutually Exclusive Events (Disjoint Events): Two events are called mutually exclusive, if the occurrence of one excludes the occurrence of others i.e. both can't occur simultaneously.
A ∩ B = φ, P(A ∩ B) =0
Equally Likely Events: If one of the events cannot happen in preference to other, then such events are said to be equally likely.
Odds in Favour of an Event = m/n
Where m → no. of ways favourable to A
n → no. of ways not favourable to A
Odds Against the Event = n/m
Probability: 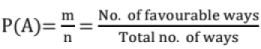
P(A)+ P(A')=1
Important points:
- P(A ∪ B) → Probability of happening of "at least one" event of A & B
- P(A ∩ B) → Probability of happening of "both” events of A & B.
- If the events are certain to happen, then the probability is unity.
- If the events are impossible to happen, then the probability is zero.
Addition Law of Probability:
- For every events A, B and C not mutually exclusive
P(A∪b∪C)= P(A) + P(B)+ P(C) - P(A ∩ B)- P(B ∩ C)- P(C ∩ A)+ P(A ∩ B ∩ C) - For the event A, B and C which are mutually exclusive
P(A U B U C)= P(A)+ P(B)+ P(C)
Independent Events: Two events are said to be independent, if the occurrence of one does not affect the occurrence of the other.
If P(A∩B) = P(A) P(B) ↔ Independent events A & B
Conditional Probability: If A and B are dependent events, then P(B/A) denotes the probability of occurrence of B when A has already occurred. This is known as conditional probability.
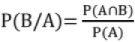
For independent events A & 13 → P(B/A) = P(B)
Theorem of Combined Probability: If the probability of an event A happening as a result of trial is P{A). Probability of an event 13 happening as a result of trial after A has happened is P(B/A) then the probability of both the events A and B happening is
P(A∩B)= P(A). P(B/A), [P(A)≠0]
= P(B). P(A/B), [P(B)≠ 0]
This is also known as Multiplication Theorem.
For independent events A & B → P(B/A) = P(B), P(A/B )= P(A)
Hence P(A∩B) = P(A) P(B)
Important Points:
If P1 & P2 are probabilities of two independent events then
- P1(1-P2) → probability of first event happens and second fails (i.e only first happens)
- (1-P1)(1-P2) → probability of both event fails
- 1-(1-P1)(1-P2) → probability of at least one event occur
- P1P2 → probability of both event occurs
Baye's theorem:
An event A corresponds to a number of exhaustive events B1, B2,.., Bn.
If P(Bi) and P(A/Bi) are given then,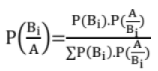
This is also known as theorem of Inverse Probability.
Random variable: Real variable associated with the outcome of a random experiment is called a random variable.
Probability Density Function (PDF) or Probability Mass Function: The set of values Xi with their probabilities Pi constitute a probability distribution or probability density function of the variable X. If f(x) is the PDF, then f(xk) = P(X = xk),
PDF has the following properties:
- Probability density function is always positive i.e. f(x) ≥ 0
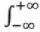 f(x) dx = 1 (Continuous)
f(x) dx = 1 (Continuous)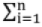 f(xi) = 1 (Discrete)
f(xi) = 1 (Discrete)
Discrete Cumulative Distribution Function (CDF) or Distribution Function
The Cumulative Distribution Function F(x) of the discrete variable x is defined by,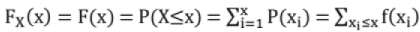
Continuous Cumulative Distribution function (CDF) or Distribution Function: If 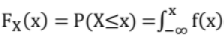 is defined as the cumulative distribution function or simply the distribution function of the continuous variable.
is defined as the cumulative distribution function or simply the distribution function of the continuous variable.
CDF has the following properties:
(i) 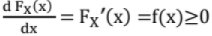
(ii) 1≥ Fx(x) ≥ 0
(iii) If x2 > x1 then Fx (x2) > Fx (x1), i.e. CDF is monotone (non-decreasing function)
(iv) Fx (-∞) = 0
(v) Fx (∞) = 1
(vi) 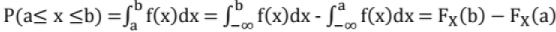
Expectation [E(x)]:
(i) E(X) = 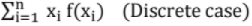
(ii) E(X) = 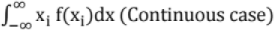
Properties of Expectation
(i) E(constant) = constant
(ii) E(CX) = C.E(X) [C is constant]
(iii) E(AX+BY) = AE(X) + BE(Y) [A & B are constants]
(iv) E(XY) = E(X)E(Y/X) = E(Y) E(X/Y)
E(XY) ≠ E(X) E(Y) in general
But E(XY) = E(X) E(Y), if X & Y are independent
Variance (Var(X))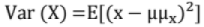
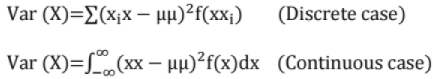
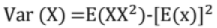
Properties of Variance
(i) Var(constant) = 0
(ii) Var(Cx) = C2 Var(x) -Variance is non-linear [here C is constant]
(iii) Var(Cx±D) = C2 Var(x) -Variance is translational invariant [C & D are constants]
(iv) Var(x-k) = Var(x) [k is constant]
(v) Var(ax+by) = a2Var(x) + b2 Var(y) ± 2ab cov(x, y) (if not independent) [A & B are constants]
= a2Var(x) + b2Var(y) (if independent)
Covariance
Cov (x, y) = E(xy)-E(x) E(y)
If independent ⇒ covariance = 0, E (xy) = E(x) . E(y)
(if covariance = 0, then the events are not necessarily independent)
Properties of Covariance
- Cov(x,y) = Cov(y.x) (i.e. symmetric)
- Cov(x,x) = Var(x)
- |Cov (x ,y)| ≤ σx σy
Standard Distribution Function (Discreter.v. case):
(i) Binomial Distribution : P(r) = nCrPrqn-r
Mean = np, Variance = npq,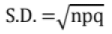
(ii) Poisson Distribution: Probability of k success is P (k) =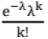
k → no. of success trials, n → no. of trials, P → success case probability
λ → mean of the distribution
For Poisson distribution: Mean = λ, variance =λ, and λ=np
Standard Distribution Function (Continuous r.v. case):
- Normal Distribution (Gaussian Distribution):
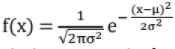
Where μ and σ are the mean and standard deviation respectively
(i) P(μ - σ < x < μ + σ) = 68%
(ii) P(μ - 2σ < x < μ + 2σ) = 95 .5%
(iii) P(μ - 3σ < x < μ + 3σ) = 99.7%
(iv) Total area under the curve is is unity i.e.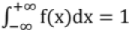
(v) P(x1 < x < x2) =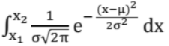 = Area under the curve from x1 to x2
= Area under the curve from x1 to x2 - Exponential distribution: f(x) = λe-λx, x ≥ 0, here λ > 0
= 0, x < 0 - Uniform distribution:
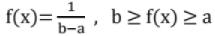 = 0, otherwise
= 0, otherwise - Cauchy distribution:
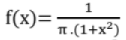
- Rayleigh distribution function:
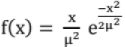 , x ≥ 0
, x ≥ 0
Mean:
- For a set of n values of a variant X = (x1, x2,...,xn)
The arithmetic mean,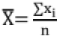
- For a grouped data if x1, x2,......., xn are mid values of the class intervals having frequencies f1, f2......fn, then,
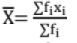
- If
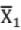 is mean for n1 : data
is mean for n1 : data 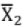 is mean for n2 data; then combined mean of n1 + n2 data is
is mean for n2 data; then combined mean of n1 + n2 data is 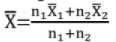
- lf
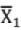 σ1 be mean and SD of a sample size n1 and m2, σ2 be those for a sample of size n2 then SD of combined sample of size n1+ n2 is given by,
σ1 be mean and SD of a sample size n1 and m2, σ2 be those for a sample of size n2 then SD of combined sample of size n1+ n2 is given by,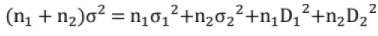
Di = mi-m (m, σ = mean, SD of combined sample)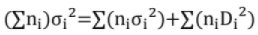
Median: When the values in a data sample are arranged in descending order or ascending order of magnitude the median is the middle term if the no. of sample is odd and is the mean of two middle terms if the number is even.
Mode: It is defined as the value in the sampled data that occurs most frequently.
Important Points:
- Mean is best measurement(∵ all observations taken into consideration).
- Mode is worst measurement (∵ only maximum frequency is taken).
- In median, 50 % observation is taken.
- Sum of the deviation about "mean" is zero.
- Sum of the absolute deviations about "median" is minimum.
- Sum of the square of the deviations about “mean" is minimum.
Co-efficient of variation 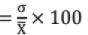
Correlation coefficient = p(x,y) = 
- -1 ≤ ρ(x,y) ≤ 1
- ρ(x,y) = ρ(y,x)
- |ρ(x, y)| = 1 when P(x = 0) = 1 ; or P (x = ay) = 1 [ for some a]
- If the correlation coefficient is -ve, then two events are negatively correlated.
- If the correlation coefficient is zero, then two events are uncorrelated.
- If the correlation coefficient is +ve, then two events are positively correlated.
Line of Regression:
The equation of the line of regression of y on x is 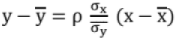
The equation of the line of Regression of x on y is 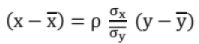
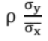 is called the regression coefficient of y on x and is denoted by byx.
is called the regression coefficient of y on x and is denoted by byx.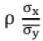 is called the regression coefficient of x on y and is denoted by bxy.
is called the regression coefficient of x on y and is denoted by bxy.
Joint Probability Distribution: If X & Y are two random variables then Joint distribution is defined as, Fxy(x, y) = P(X ≤ x ; Y ≤ y)
Properties of Joint Distribution Function/ Cumulative Distribution Function:
(i) Fxy (-∞, -∞) = 0
(ii) Fxy(∞, ∞) = 1
(iii) Fxy(-∞, ∞) = 0 {Fxy (-∞, ∞) = P(X ≤ -∞; Y ≤ y) = 0 x 1 = 0}
(iv) Fxy(x, ∞) = P(X ≤ x ; Y ≤ ∞) = Fx(x).1 = Fx(x)
(v) Fxy(∞, y) = Fy(y)
Joint Probability Density Function:
Defined as f(x, y) = 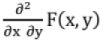
Property: 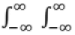 f(x, y) dx dy = 1
f(x, y) dx dy = 1
Note: X and Y are said to be independent random variable
If fxy(x,y) = fx(x). fy(y)
3. Numerical Methods
3. Numerical Methods
1. Solution of Algebraic and Transcendental Equation / Root Finding;
Consider an equation f(x) = 0
(i) Bisection method
This method finds the root between points "a" and "b".
If f(x) is continuous between a and b and f (a) and f (b) are of opposite sign then there is a root between a & b (Intermediate Value Theorem).
First approximation to the root is x1 =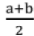 .
.
If f(x1) = 0, then x1 is the root of f(x) = 0, otherwise root lies between a and x1 or x1 and b.
Similarly x2 and x3 ...... are determined.
- Simplest iterative method
- Bisection method always converge, but often slowly.
- This method can't be used for finding the complex roots.
- Rate of convergence is linear
(ii) Newton Raphson Method (or Successive Substitution Method or Tangent Method)
- This method is commonly used for its simplicity and greater speed.
- Here f(x) is assumed to have continuous derivative f(x).
- This method fails if f'(x) = 0.
- It has second order of convergence or quadratic convergence, i.e. the subsequent error at each step is proportional to the square of the error at previous step.
- Sensitive to starting value, i.e. The Newton's method converges provided the initial approximation is chosen sufficiently close to the root.
- Rate of convergence is quadratic.
(iii) Secant Method
- Convergence is not guaranteed.
- If converges, convergence super linear (more rapid than linear, almost quadratic like Newton Raphson, around 1.62).
(iv) Regula Falsi Method or (Method of False Position)
- Regula falsi method always converges.
- However, it converges slowly.
- If converges, order of convergence is between 1 & 2 (closer to 1).
- It is superior to Bisection method.
Given f(x) = 0
Select x0 and x1 such that f(x0) f(x1) < 0 (i.e. opposite sign)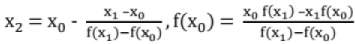
Check if f(x0) f(x2) < 0 or f(x1) f(x2) < 0
Compute x3 ....
which is an approximation to the root.
2. Solution of Linear System of Equations
(i) Gauss Elimination Method
Here equations are converted into "upper triangular matrix" form, then solved by "back substitution" method.
Consider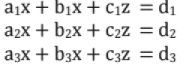
Step 1: To eliminate x from second and third equation (we do this by subtracting suitable multiple of first equation from second and third equation)
a1x + b1y + c1z = d1. (pivotal equation, a1 pivot point)
b2y + c2'z = d2.
b3y + c3'z = d3.
Step 2: Eliminate y from third equation
a1x + b1y + c1z = d1.
b2.y + C2z = d2. (pivotal equation, b2' is pivot point.)
c3'z = d3"
Step 3: The value of x , y and z can be found by back substitution.
Note: Number of operations: 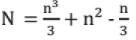
(ii) Gauss ]ordon Method
- Used to find inverse of the matrix and solving linear equations.
- Here back substitution is avoided by additional computations that reduce the matrix to "diagonal from", instead to triangular form in Gauss elimination method.
- Number of operations is more than Gauss elimination as the effort of back substitution is saved at the cost of additional computation.
Step 1: Eliminate x from 2nd and 3rd
Step 2: Eliminate y from 1st and 3rd
Step 3: Eliminate z from 1st and 2nd
(iii) L U Decomposition
- It is modification of the Gauss eliminiation method.
- Also Used for finding the inverse of the matrix.
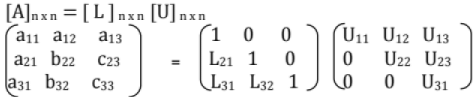
Ax = LUX = b can be written as
a)LY=b and
b) UX=Y
Solve for Y from a) then solve for X from b). This method is known as Doolittle's method. - Similar methods are Grout's method and Cholesky methods.
(iv) Iterative Method
- Jacobi Iteration Method
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3Z = d3
If a1, b2, c3 are large compared to other coefficients, then solving these for x, y, z respectively
x = k1 - l1y - m1z
y = k2 - l2x - m2z
z = k3 - l3x - m3y
Let us start with initial approximation xo, yo, zo
x1= k1 - l1y0 - m1z0
y1= k2 - l2y0 - m2z0
z1 = k3 - l3y0 - m3z0
Note: No component of x(k) is used in computation unless y(k) and z(k) are computed.
The process is repeated till the difference between two consecutive approximations is negligible.
In generalized form: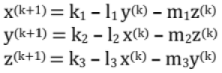
- Gauss-Siedel Iteration Method
Modification of the Jacobi's Iteration Method
Start with (x0, y0, z0) = (0, 0, 0) or anything [No specific condition]
In first equation, put y = y0 z = z0 which will give x1
In second equation, put x = x1 and z = z0 which will give y1
In third equation, put x = x1 and y = y1 which will give z1
Note: To compute any variable, use the latest available value.
In generalized form: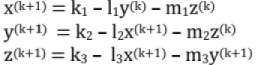
3. Numerical Integration
Trapezoidal Formula: Step size h = 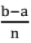
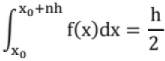 {(first term + last term) + 2 (remaining terms)}
{(first term + last term) + 2 (remaining terms)}
Error = Exact - approximate
The error in approximating an integral using Trapezoidal rule is bounded by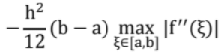
Simpson's One Third Rule (Simpson's Rule):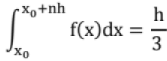 {(first term + last term) + 4 (all odd terms) + 2 (all even terms)}
{(first term + last term) + 4 (all odd terms) + 2 (all even terms)}
The error in approximating an integral using Simpson's one third rule is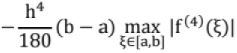
Simpson's Three Eighth Rule: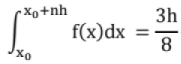 {(first term + last term) + 2 (all multiple of 3 terms)+3 (all remaining terms)}
{(first term + last term) + 2 (all multiple of 3 terms)+3 (all remaining terms)}
The error in approximating an integral using Simpson's 3/8 rule is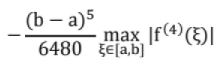
4. Solving Differential Equations
(i) Euler method (for first order differential equation)
Given equation is y' = f(x, y); y(x0) = y0
Solution is given by, Yn+i = yn + h f(xn, yn)
(ii) Rimge Kutta Method
Used for finding the y at a particular x without solving the 1st order differential equation 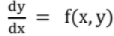
K1 = h f(x0, y0)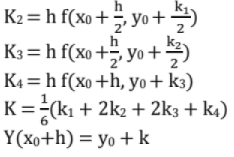
|
1 videos|30 docs|57 tests
|