LAMINAR FLOW
Fluid particles move along straight parallel paths in layers or laminae It occurs at low velocity; Viscosity force predominates inertial force. Relation between Shear and Pressure Gradients in Laminar Flow For a steady uniform flow,
dt/dy = Δp/ΔxThus, for a steady uniform laminar flow the pressure gradient in the direction of flow is equal to the shear stress gradient in the normal direction. By using newton’s law of viscosity :
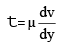 The differential equation of laminar flow is given by,
The differential equation of laminar flow is given by,
μd2v/dy2 = Δp/Δx
Steady Laminar Flow in Circular Pipes (Nagen - Poiseulle flow) In a circular pipe with steady laminar flow, the shear stress t varies linearly along the radius of the pipe as,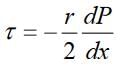 The maximum value of stress t0 occurs at r = R (i.e., at the walls of the pipe),
The maximum value of stress t0 occurs at r = R (i.e., at the walls of the pipe),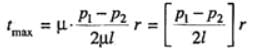 The negative sign on x indicates decrease in pressure in the direction of flow..
The negative sign on x indicates decrease in pressure in the direction of flow..
The pressure must decrease because pressure force is the only means available to compensate for resistance to the flow, the potential and kinetic energy remain constant. Fully developed horizontal pipe flow is merely a balance between pressure and viscous forces–the pressure difference acting on the end of the cylinder of area πr2 and the shear stress acting on the lateral surface of the cylinder of area 2πrl. This force balance can be written asp1πr2−(p1−∆p)πr2−2πr/τ=0 ∴ Δp/l= 2τ/rFor laminar flow of a Newtonian fluid, the shear stress is simply proportional to the velocity gradient,τ=μdu/dy. In the notation associated with our pipe flow, this becomes τ=−μdu/dr By combining the above two equations, we obtain du/dr=−(∆p/2μl)which can be integrated to give the velocity profile: u=−(∆p/4μl).r2 + C1 where C1 is a constant. Because the fluid is viscous, it sticks to the pipe wall so that 'u=0' at 'r=D/2'. Thus, C1=4R2.(∆p/16μl). Hence, the velocity profile can be written as 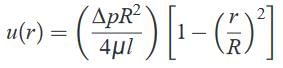 And,
And,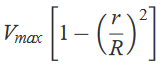 where Vmax= (ΔpR2/4μl) is the centerline velocity i.e. at the center of the pipe.By definition, the average velocity is the flow rate divided by the cross-sectional area,V=qv/πR2 so that for this flow,
where Vmax= (ΔpR2/4μl) is the centerline velocity i.e. at the center of the pipe.By definition, the average velocity is the flow rate divided by the cross-sectional area,V=qv/πR2 so that for this flow,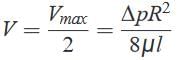 The point where local velocity is equal to average velocity is given by,
The point where local velocity is equal to average velocity is given by,
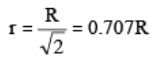 so mean velocity of flow occurs at a radial distance of 0.707 R from the centre of the pipe. Pressure drops
so mean velocity of flow occurs at a radial distance of 0.707 R from the centre of the pipe. Pressure drops 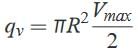 Putting the value of vmax in the above equation,
Putting the value of vmax in the above equation,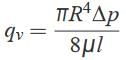 This above equation is commonly referred to as Hagen-Poiseuille’s law. The velocity and shear stress distribution are as shown below :
This above equation is commonly referred to as Hagen-Poiseuille’s law. The velocity and shear stress distribution are as shown below :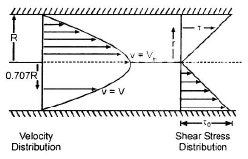 Laminar Flow Between Parallel Plates
Laminar Flow Between Parallel Plates
Case 1 : Both plates are at Rest Using the Navier-Stokes equations, we can determine the flow between two fixed horizontal, infinite parallel plates. In order to to this, we will need to describe how the fluid particles move. For this case, there will be no flow in the y or z direction; v = 0 and w = 0. As a result, all of the fluid flow will be in the x-direction. Hence, the resulting continuity equation will be ∂u/∂x=0. In addition, u will have no variation in the z-direction for the infinite plates. This means that the stead flow ∂u/∂t = 0 so that u = u(y) Taking these conditions into account the Navier-Stokes equation will be reduced the following equations.(Eq 1) = -∂p/x+u (∂2u/∂y2) (Eq 2) = -∂p∂y - ρg (Eq 3) = -∂p∂zIn these equations, gx=0, gy = -g, and gz=0.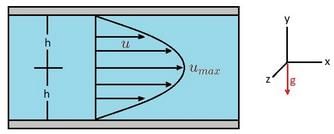 As a result, the y-axis will point up. Next, we will integrate equation 2 and 3 to generate the following equation. In turn, this shows that there is a variation of pressure hydrostatically in the y-direction.Next, equation 1 will be rewritten into the following form and integrated twice.After integrating and determining all the constants,the velocity distribution can be fully derived.
As a result, the y-axis will point up. Next, we will integrate equation 2 and 3 to generate the following equation. In turn, this shows that there is a variation of pressure hydrostatically in the y-direction.Next, equation 1 will be rewritten into the following form and integrated twice.After integrating and determining all the constants,the velocity distribution can be fully derived. In turn, the resulting velocity profile between the fixed plates is parabolic.Volume Rate of Flow: The volume flow rate ,q, represents the total volume of fluid pass between the two plates.
In turn, the resulting velocity profile between the fixed plates is parabolic.Volume Rate of Flow: The volume flow rate ,q, represents the total volume of fluid pass between the two plates. 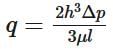 Mean Velocity: In turn, taking in consideration that the pressure gradient is inversely proportional to the viscosity and has a strong dependence on the gap width, the mean velocity can be determined.
Mean Velocity: In turn, taking in consideration that the pressure gradient is inversely proportional to the viscosity and has a strong dependence on the gap width, the mean velocity can be determined. 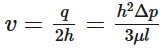 Maximum Velocity: Finally, maximum velocity will occur at y = 0 between the two the parallel plates. As a result, the maximum velocity can be expressed in the following mathematical form.
Maximum Velocity: Finally, maximum velocity will occur at y = 0 between the two the parallel plates. As a result, the maximum velocity can be expressed in the following mathematical form. 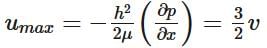 The pressure drop between any two points distance L apart is given by
The pressure drop between any two points distance L apart is given by 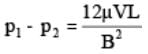 The distribution of shear stress is given by
The distribution of shear stress is given by 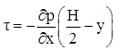 The shear stress is maximum at y = 0 and is given by : t0 = (∂p/∂x)(B/2) Case 2 : When one Plate Moving And Other at Rest is known as COUETTE Flow The velocity distribution in COUETTE FLOW is shown below :
The shear stress is maximum at y = 0 and is given by : t0 = (∂p/∂x)(B/2) Case 2 : When one Plate Moving And Other at Rest is known as COUETTE Flow The velocity distribution in COUETTE FLOW is shown below :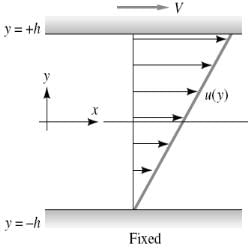 Consider two-dimensional incompressible plane(∂/∂z=0) viscous flow between parallel plates a distance 2h apart, as shown in fig.. We assume that the plates are very wide and very long , so the flow is essentially axial, u≠0 but v=w=0. The present case is where the upper plate moves at velocity 'V' but there is no pressure gradient. Now, by applying the continuity equation and integrating, then finding the constants, we get the velocity distribution:
Consider two-dimensional incompressible plane(∂/∂z=0) viscous flow between parallel plates a distance 2h apart, as shown in fig.. We assume that the plates are very wide and very long , so the flow is essentially axial, u≠0 but v=w=0. The present case is where the upper plate moves at velocity 'V' but there is no pressure gradient. Now, by applying the continuity equation and integrating, then finding the constants, we get the velocity distribution: 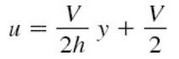 (for -h ≤ y ≥ +h)Expression For Head Loss
(for -h ≤ y ≥ +h)Expression For Head Loss
(a) In case of laminar flow through pipes :hf = 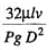 (b) In case of laminar flow through parallel plates : hf =
(b) In case of laminar flow through parallel plates : hf =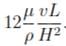 (c) In case of open channel flow : hf =
(c) In case of open channel flow : hf =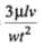 (d) The general equation is
(d) The general equation is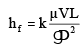 where, hf = loss of head in length L
where, hf = loss of head in length L
V = mean velocity of flow
D = characteristic dimension representing the geometry of passage.
k = constant, whose value depends upon the shape of passage.
The differential equation of laminar flow is given by,
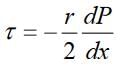 The maximum value of stress t0 occurs at r = R (i.e., at the walls of the pipe),
The maximum value of stress t0 occurs at r = R (i.e., at the walls of the pipe),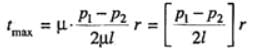 The negative sign on x indicates decrease in pressure in the direction of flow..
The negative sign on x indicates decrease in pressure in the direction of flow..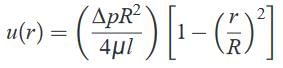 And,
And,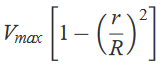 where Vmax= (ΔpR2/4μl) is the centerline velocity i.e. at the center of the pipe.By definition, the average velocity is the flow rate divided by the cross-sectional area,V=qv/πR2 so that for this flow,
where Vmax= (ΔpR2/4μl) is the centerline velocity i.e. at the center of the pipe.By definition, the average velocity is the flow rate divided by the cross-sectional area,V=qv/πR2 so that for this flow,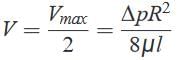 The point where local velocity is equal to average velocity is given by,
The point where local velocity is equal to average velocity is given by,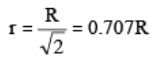 so mean velocity of flow occurs at a radial distance of 0.707 R from the centre of the pipe. Pressure drops
so mean velocity of flow occurs at a radial distance of 0.707 R from the centre of the pipe. Pressure drops 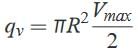 Putting the value of vmax in the above equation,
Putting the value of vmax in the above equation,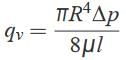 This above equation is commonly referred to as Hagen-Poiseuille’s law. The velocity and shear stress distribution are as shown below :
This above equation is commonly referred to as Hagen-Poiseuille’s law. The velocity and shear stress distribution are as shown below :Laminar Flow Between Parallel Plates
 As a result, the y-axis will point up. Next, we will integrate equation 2 and 3 to generate the following equation. In turn, this shows that there is a variation of pressure hydrostatically in the y-direction.Next, equation 1 will be rewritten into the following form and integrated twice.After integrating and determining all the constants,the velocity distribution can be fully derived.
As a result, the y-axis will point up. Next, we will integrate equation 2 and 3 to generate the following equation. In turn, this shows that there is a variation of pressure hydrostatically in the y-direction.Next, equation 1 will be rewritten into the following form and integrated twice.After integrating and determining all the constants,the velocity distribution can be fully derived. In turn, the resulting velocity profile between the fixed plates is parabolic.Volume Rate of Flow: The volume flow rate ,q, represents the total volume of fluid pass between the two plates.
In turn, the resulting velocity profile between the fixed plates is parabolic.Volume Rate of Flow: The volume flow rate ,q, represents the total volume of fluid pass between the two plates. 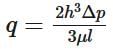 Mean Velocity: In turn, taking in consideration that the pressure gradient is inversely proportional to the viscosity and has a strong dependence on the gap width, the mean velocity can be determined.
Mean Velocity: In turn, taking in consideration that the pressure gradient is inversely proportional to the viscosity and has a strong dependence on the gap width, the mean velocity can be determined. 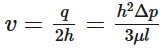 Maximum Velocity: Finally, maximum velocity will occur at y = 0 between the two the parallel plates. As a result, the maximum velocity can be expressed in the following mathematical form.
Maximum Velocity: Finally, maximum velocity will occur at y = 0 between the two the parallel plates. As a result, the maximum velocity can be expressed in the following mathematical form. 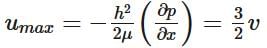 The pressure drop between any two points distance L apart is given by
The pressure drop between any two points distance L apart is given by 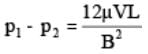 The distribution of shear stress is given by
The distribution of shear stress is given by 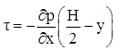 The shear stress is maximum at y = 0 and is given by : t0 = (∂p/∂x)(B/2) Case 2 : When one Plate Moving And Other at Rest is known as COUETTE Flow The velocity distribution in COUETTE FLOW is shown below :
The shear stress is maximum at y = 0 and is given by : t0 = (∂p/∂x)(B/2) Case 2 : When one Plate Moving And Other at Rest is known as COUETTE Flow The velocity distribution in COUETTE FLOW is shown below : Consider two-dimensional incompressible plane(∂/∂z=0) viscous flow between parallel plates a distance 2h apart, as shown in fig.. We assume that the plates are very wide and very long , so the flow is essentially axial, u≠0 but v=w=0. The present case is where the upper plate moves at velocity 'V' but there is no pressure gradient. Now, by applying the continuity equation and integrating, then finding the constants, we get the velocity distribution:
Consider two-dimensional incompressible plane(∂/∂z=0) viscous flow between parallel plates a distance 2h apart, as shown in fig.. We assume that the plates are very wide and very long , so the flow is essentially axial, u≠0 but v=w=0. The present case is where the upper plate moves at velocity 'V' but there is no pressure gradient. Now, by applying the continuity equation and integrating, then finding the constants, we get the velocity distribution: 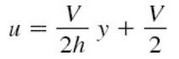 (for -h ≤ y ≥ +h)Expression For Head Loss
(for -h ≤ y ≥ +h)Expression For Head Loss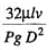 (b) In case of laminar flow through parallel plates : hf =
(b) In case of laminar flow through parallel plates : hf =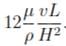 (c) In case of open channel flow : hf =
(c) In case of open channel flow : hf =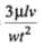 (d) The general equation is
(d) The general equation iswhere, hf = loss of head in length L





















