Theory of Columns | Mechanical Engineering SSC JE (Technical) PDF Download
THEORY OF COLUMNS
Compression Member : A compression member is a structural member which is straight and subjected to two equal and opposite compressive forces applied at its ends.
Column: It is defined as a vertical member which is fixed at both the ends and subjected to an axial compressive load.Column, is a compression member that is so slender compared to its length that under gradually increasing loads, it fails by buckling at loads
considerably less that those required to cause failure by crushing.
• A compression member is generally considered to be a long column when its unsupported length is more than 10 times its least lateral dimension.
• Column, Stanchion or post is a vertical compression member supporting floors or girders in a building.
• Principal rafter is a top chord member in a roof truss.
• Boom is the principal compression member in a crane.
• Strut is commonly used for compression member in a roof truss. It may either be in vertical position or in inclined position.
MODES OF FAILURE OF A COLUMN
Elastic instability
A column subjected to axial load, may fail under the following modes:
(i) Crushing
(ii) Buckling
(iii) Mixed mode of Buckling and Crushing.
Euler's Theory (Buckling failure)
- Assumption of Euler's theory:
(i) Axis of the column is perfectly straight when unloaded.
(ii) The line of thrust coincides exactly with the unstrained of the column.
(iii) Flexural rigidity EI is uniform
(iv) Material is isotropic and homogeneous.
(v) The buckling value of load is assumed to obtain for all degrees of flexure.
(vi) Length is assumed to be too large with respect to cross section.
- Limitation of Euler's Formula:
(i) The critical load that causes buckling depends not on strength of the material, but only on its dimensions and modulus of elasticity. This converts the strut problem from the problem of instability to a problem of stress, of which Euler's theory takes no account.
(ii) In order for Euler's formula to be applicable, the critical stress p1 must not exceed the proportional limit.
IDEAL END CONSITION & EFFECTIVE LENGTH
Depending upon various combinations of restraints, there may be the following four cases of end condition:
End condition Euler's load or critical load Equivalent length (Le)
Case 1 : Both ends hinged
Case 2 : One end fixed and other end free
Case 3 : Both ends fixed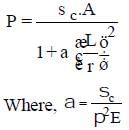
PRACTICAL END CONSITION AND EFFECTIVE LENGTH FACTORS:
As per IS : 800 - 1984, following table can be used for finding effective length:
Effective length of compression members
Radius of Gyration and Slenderness Ratio:
- The radius of gyration of a section is given by
where, I = Moment of Inertia
A = area of section
- Rankine's formula
The Rankine's formula is applicable for all columns ranging form very short to very long struts.
Ranking proposed,
Where, Pc = fc.A= ultimate load for a strut
= Euler crippling load for the standard case
After rearranging above relations,
= Rankine's constant for a particular material
|
6 videos|104 docs|59 tests
|
FAQs on Theory of Columns - Mechanical Engineering SSC JE (Technical)
| 1. What is the theory of columns in mechanical engineering? |  |
| 2. What are the different types of column failure modes? |  |
| 3. How is the load-carrying capacity of a column determined? |  |
| 4. What factors affect the stability of a column? |  |
| 5. How does column slenderness affect its behavior? |  |
















