Force and Laws of Motion Class 9 Notes Science Chapter 8
Introduction to Motion and Force
Motion is described in terms of position, velocity, and acceleration. Motion can be uniform (consistent speed) or non-uniform (changing speed).Historical Perspective:
- Ancient Belief: Objects at rest are in their "natural state."
- Galileo & Newton: Challenged the old belief, developing new understanding of motion and its causes.
A force is an effort that changes the state of an object at rest or at motion. It can change an object’s direction and velocity. Force can also change the shape of an object.
It is the force that enables us to do any work.
To do anything, either we pull or push the object. Therefore, pull or push is called force.
Example: To open a door, either we push or pull it. A drawer is pulled to open and pushed to close.
 Push or Pull is called Force
Push or Pull is called ForceEffects of Force
- Force can make a stationary body move.
- Force can stop a moving body.
- Force can change the direction of a moving object.
 Effects of Force
Effects of Force
- Force can change the speed of a moving body.
- Force can change the shape and size of an object.
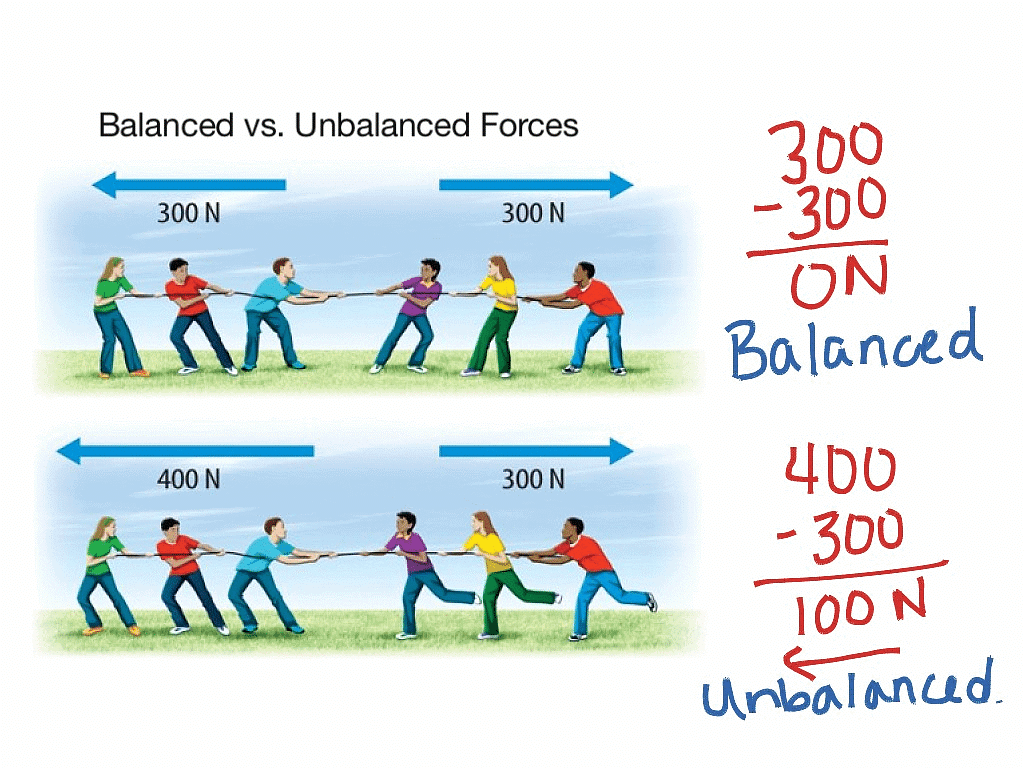
Balanced and Unbalanced Forces
In physics, forces can be classified as balanced or unbalanced based on their effects on an object's motion. Mentioned below are the details of both these forces:
 Balanced and Unbalanced Forces
Balanced and Unbalanced Forces
Balanced Forces
If the resultant of applied forces is equal to zero, it is called balanced forces.
 Balanced Force
Balanced Force
- Example: In the tug of war if both teams apply similar magnitude of forces in opposite directions, the rope does not move in either side. This happens because of balanced forces in which the resultant of applied forces becomes zero.
- Balanced forces do not cause any change in the state of an object. Balanced forces are equal in magnitude and opposite in direction.
- Balanced forces can change the shape and size of an object.
Example: When forces are applied from both sides over a balloon, the size and shape of the balloon are changed.
Unbalanced Forces
If the resultant of applied forces are greater than zero, the forces are called unbalanced forces. An object at rest can be moved because of applying unbalanced forces.
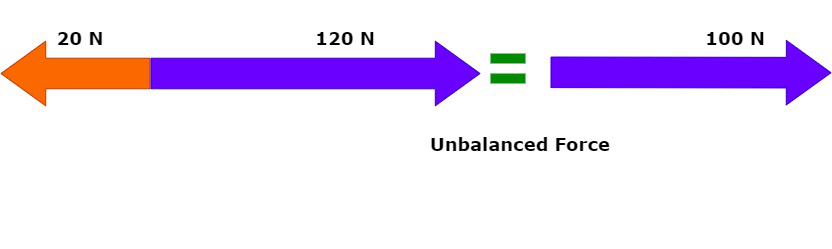 Unbalanced Force
Unbalanced Force
Unbalanced forces can do the following:
- Move a stationary object.
- Increase the speed of a moving object.
- Decrease the speed of a moving object.
- Stop a moving object.
- Change the shape and size of an object.
Newton’s Laws of Motion
Newton studied the ideas of Galileo and gave the three laws of motion. These laws are known as Newton’s laws of motion:
(i) Newton’s First Law of Motion (Law of Inertia).
(ii) Newton’s Second Law of Motion.
(iii) Newton’s Third Law of Motion.
First Law of Motion (Law of Inertia)
Any object remains in the state of rest or uniform motion along a straight line until it is compelled to change the state by applying an external force.
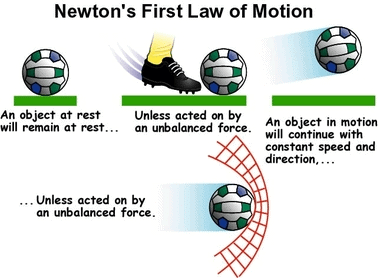 Illustration of Newton's First Law of Motion
Illustration of Newton's First Law of Motion
Explanation
- If any object is in the state of rest, then it will remain in rest until an external force is applied to change its state.
- Similarly, an object will remain in motion until an external force is applied over it to change its state.
- This means all objects resist changing their state. The state of any object can be changed by applying external forces only.
Examples of Newton’s First Law of Motion in Everyday Life
- A person standing inside a bus falls backwards when the bus starts moving suddenly.
Explanation: This happens because the person and bus both are at rest while the bus is not moving, but as the bus starts moving, the legs of the person start moving along with the bus, but the rest portion of his body has the tendency to remain in rest. Because of this, the person falls backwards; if he is not alert. - A person standing inside a moving bus falls forward if the driver applies brakes suddenly.
Explanation: This happens because when the bus is moving, the person standing in it is also in motion along with the bus. But when the driver applies brakes the speed of the bus decreases suddenly or the bus comes into a state of rest suddenly, in this condition the legs of the person, which are in contact with the bus come to rest while the rest part of his body tends to remain in motion. Because of this person falls forward if he is not alert. - Before hanging the wet clothes over the laundry line, usually, many jerks are given to the clothes to get them dried quickly. Because of jerks, droplets of water from the pores of the cloth fall on the ground, and a reduced amount of water in clothes dries them quickly.
Explanation: This happens because when suddenly clothes are made in motion by giving jerks, the water droplets in them have the tendency to remain at rest and they are separated from the clothes and fall on the ground. - When a striker hits the pile of coins on the carom-board, the coin only at the bottom moves away leaving the rest of the pile of the coin in the same place.
Explanation: This happens because when the pile is struck with a striker, the coin at the bottom comes in motion while the rest of the coin in the pile has the tendency to remain in the rest and they vertically fall on the carom-board and remain at the same place.
Galileo's Idea of Motion
Galileo first said that objects move at a constant speed when no forces act on them.
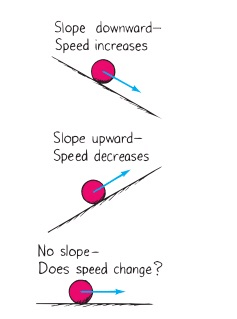 Galileo's Idea of Motion
Galileo's Idea of Motion
- This means if an object is moving on a frictionless path and no other force is acting upon it, the object will be moving forever. That is, there is no unbalanced force working on the object.
- But practically it is not possible for any object. Because to attain the condition of zero, the unbalanced force is impossible.
- Force of friction, Force of air, and many other forces are always acting upon an object.
Inertia and Mass
- The property of an object because of which it resists getting disturbed in its state is called inertia.
In other words, the natural tendency of an object that resist the change in the state of motion or rest of the object is called inertia. - The inertia of an object is measured by its mass. Inertia is directly proportional to the mass of the object.
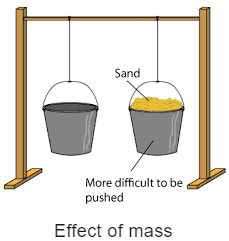
Inertia increases with an increase in mass and decreases with a decrease in mass.
- A heavy object will have more inertia than the lighter one.
Since a heavy object has more inertia, thus it is more difficult to push or pull a heavy box over the ground than the lighter one. - Inertia is the natural tendency of an object to resist a change in its state of motion or of rest. The mass of an object is a measure of its inertia.
Second Law of Motion
The rate of change of momentum of an object is proportional to the applied unbalanced force in the direction of the force.
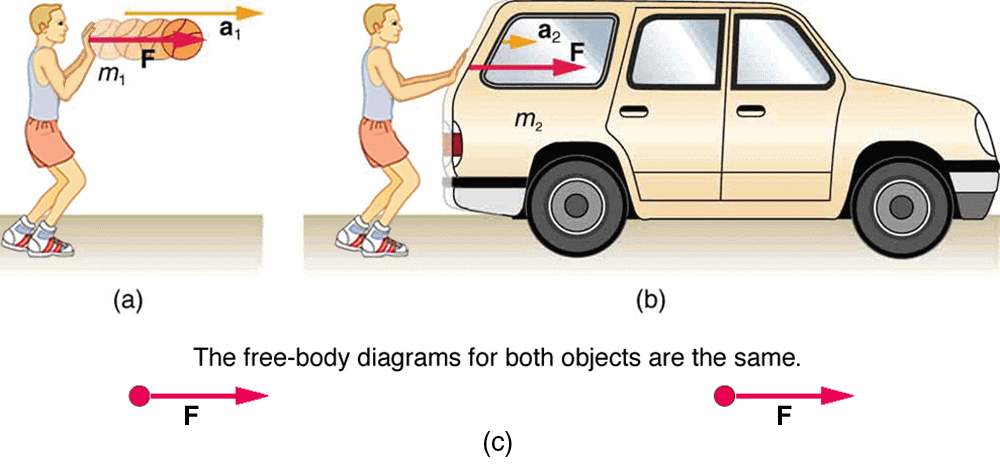 Illustration of Force depending on Mass and Acceleration
Illustration of Force depending on Mass and Acceleration(a) Momentum
- Momentum is the power of motion of an object.
- The product of velocity and mass is called momentum.
Momentum is denoted by ‘p’. - Therefore, Momentum of the object = Mass × Velocity (p = m × v),
where p = momentum, m = mass of the object and v = velocity of the object.
Some explanations to understand the momentum:
- A person gets injured in the case of hitting a moving object, such as a stone, pebbles, or anything because of the momentum of the object.
- Even a small bullet can kill a person when it is fired from a gun because of its momentum due to great velocity.
- A person gets injured severely when hit by a moving vehicle because of the momentum of the vehicle due to mass and velocity.
(b) Momentum and Mass
- Since momentum is the product of mass and velocity (p = m × v) of an object. This means momentum is directly proportional to mass and velocity. Momentum increases with the increase of either the mass or velocity of an object.
- This means if a lighter and a heavier object is moving with the same velocity, then the heavier object will have more momentum than the lighter one.
- If a small object is moving with great velocity, it has tremendous momentum. And because of momentum, it can harm an object more severely.Example: A small bullet having a small mass even kills a person when it is fired from a gun.
- Usually, road accidents prove more fatal because of high speed than slower speed. This happens because vehicles running at high speed have greater momentum compared to a vehicles running at a slower speed.
(c) Unit of Momentum
- We know that,
Momentum (p) = m × v - SI unit of mass = kg
- SI unit of velocity = m/s
Therefore,
p = kg × m/s ⇒ p = kgm/s
The momentum of an object which is in the state of rest:
Let, an object with mass ‘m’ be in the rest.
Since, the object is at rest, therefore, its velocity, v = 0
∵ Momentum = mass × velocity
⇒ p = m × 0 = 0
Thus, the momentum of an object in the rest, i.e. non-moving is equal to zero.
Numerical Problems Based on Momentum
Solution: Mass (m) = 10 kg, Velocity (v) = 2 m/s.
∵ Momentum (p) = Mass (m) × Velocity (v)
⇒ p = 10 kg × 2 m/s = 20 kg m/s.
Thus, the momentum of the stone = 20 kg m/s.
Example 2: Calculate the momentum of a bullet of 25 g when it is fired from a gun with a velocity of 100 m/s.
Solution: Given the velocity of the bullet (v) = 100 m/s,
Mass of the bullet (m) = 25 g = 25/1000 kg = 0.025 kg.
∵ p = m × v
⇒ p = 0.025 × 100 = 2.5 kg m/s.
Thus, the Momentum of the bullet = 2.5 kg m/s.
Example 3: Calculate the momentum of a bullet having a mass of 25 g is thrown using a hand with a velocity of 0.1 m/s.
Solution: Given the velocity of the bullet (v) = 0.1 m/s,
Mass of the bullet (m) = 25 g = 25/1000 kg = 0.025 kg.
∵ Momentum (p) = Mass (m) × Velocity (v)
⇒ p = 0.025 kg × 0.1 = 0.0025 kg m/s
Thus, Momentum of the bullet = 0.0025 kg m/s.
Example 4: The mass of a goods lorry is 4000 kg and the mass of goods loaded on it is 20000 kg. If the lorry is moving with a velocity of 2 m/s, what will be its momentum?
Solution: Velocity (v) = 2 m/s
⇒ Mass of lorry = 4000 kg
⇒ Mass of goods on the lorry = 20000 kg.
⇒ Total mass (m) on the lorry = 4000 kg + 20000 kg = 24000 kg
∵ Momentum (p) = Mass (m) × Velocity (v)
⇒ p = 24000 kg × 2 = 48000 kg m/s
Thus, the Momentum of the lorry = 48000 kg m/s.
Example 5: A car having a mass of 1000 kg is moving with a velocity of 0.5 m/s. What will be its momentum?
Solution: Velocity of the car (v) = 0.5 m/s
⇒ Mass of the car (m) = 1000 kg.
∵ Momentum (p) = Mass (m) × Velocity (v)
⇒ p = 1000 kg × 0.5 m/s = 500 kg m/s
Thus, the Momentum of the car = 500 kg m/s.
Mathematical Formulation of the Second Law of Motion
Suppose the mass of an object = m kg
Initial velocity of an object = u m/s,
The final velocity of an object = v m/s.
Initial momentum, p1 = mu, Final momentum, p2 = mv.
Change in momentum = Final momentum – Initial momentum
Change in momentum = mv – mu = m(v – u)
Rate of change of momentum = Change in momentum/Time taken
Rate of change of momentum = m(v-u)/t
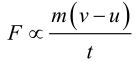
Newton's Second Law of Motion
We know that:a = (v-u)/t (From 1st equation of motion)
⇒ F = kma, where k is a constant.
Its value can be assumed as 1.
⇒ F = 1 × m × a = ma
The first law states that if external force F = 0, then a moving body keeps moving with the same velocity, or a body at rest continues to be at rest.
⇒ F = 0
We know, F = m(v-u)/t
- A body is moving with initial velocity u then,
m(v-u)/t = 0 ⇒ v – u = 0
⇒ v = u
Thus, the final velocity is also the same. - A body is at rest i.e., u = 0
⇒ u = v = 0
Hence, the body will continue to be at rest.
Third Law of Motion
- According to Newton's Third Law of Motion, for every action, there is an equal and opposite reaction.
- Newton's Third Law of Motion explains the interaction between two objects when a force is applied.
- Action and Reaction Forces:
- When one object exerts a force on another, the second object exerts an equal and opposite force back on the first.
- These forces are equal in magnitude but opposite in direction.
- These forces act on different objects, never on the same object. - Example:
Gun Recoil:- When a gun is fired, it exerts a forward force on the bullet.
- The bullet exerts an equal and opposite force on the gun, causing it to recoil.
- The gun's greater mass results in less acceleration compared to the bullet.

Applications
- Walking is enabled by the 3rd law.
- A boat moves back when we deboard it.
- A gun recoils.
- Rowing of a boat.
|
84 videos|478 docs|60 tests
|
FAQs on Force and Laws of Motion Class 9 Notes Science Chapter 8
| 1. What is the difference between balanced and unbalanced forces? |  |
| 2. How does Newton's First Law of Motion relate to the concept of inertia? |  |
| 3. Can you explain the relationship between mass and inertia? |  |
| 4. How does Newton's Second Law of Motion relate force, mass, and acceleration? |  |
| 5. Can you provide an example of Newton's Third Law of Motion in action? |  |






















