Algebraic Expressions Chapter Notes | Mathematics for Grade 10 PDF Download
 Algebraic Expressions
Algebraic Expressions
Revision: Notation for Representing Sets
Sets describe collections of numbers or objects, often used in technical fields to define ranges (e.g., resistor tolerance or engine torque). Mathematical notation uses symbols to convey precise meanings.Set Representations
- Number Line: Visualizes a range with open dots (◯) for excluded values (<, >) and closed dots (●) for included values (≤, ≥).
- Interval Notation: Uses parentheses ( ) for open intervals (excluded endpoints) and brackets [ ] for closed intervals (included endpoints). Example: (-2, 3] means -2 < x ≤ 3.
- Set Builder Notation: Describes a set as {x | condition}. Example: {x | -2 < x ≤ 3} reads “the set of all x such that x is greater than -2 and less than or equal to 3.”
Examples:
- Resistor tolerance: 135 Ω to 165 Ω is [135, 165] or {x | 135 ≤ x ≤ 165}.
- Engine torque: 0 to 2000 lb-ft is [0, 2000] or {x | 0 ≤ x ≤ 2000}.
- Rail length: 119.99 m to 120.018 m is [119.99, 120.018] or {x | 119.99 ≤ x ≤ 120.018}.
Key Terms
- Open Interval: Excludes endpoints (e.g., (-2, 3) for -2 < x < 3).
- Closed Interval: Includes endpoints (e.g., [-2, 3] for -2 ≤ x ≤ 3).
Using Algebraic Expressions
Algebraic expressions combine variables, constants, and operations to model real-world situations, such as calculating sales in woodworking.Real-World Application
Example: Gumani, a woodworker, sells jewellery boxes. His rule for the number of boxes sold is “200 minus one-fifth of the selling price.” For a price of x rand, the number sold is (-1/5)x + 200.
Table Analysis:
- At R400, 120 boxes sold; at R450, 110 sold; at R500, 100 sold; at R550, 90 sold.
- Pattern: For every R50 increase in price, sales decrease by 10 boxes. For every R10 decrease, sales increase by 2 boxes.
- Predictions: At R300, sales = 200 - (1/5) × 300 = 140 boxes. At R100, sales = 200 - (1/5) × 100 = 180 boxes. For 200 boxes, price = R0. For 0 boxes, price = R1000.
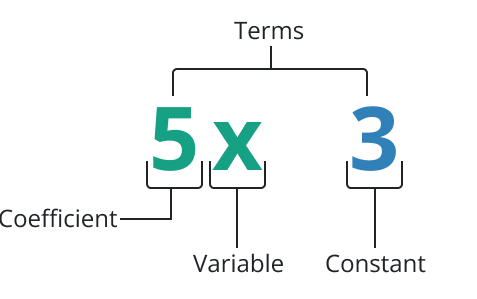
Components of Expressions
- Variables: Quantities that vary (e.g., x for selling price).
- Constants: Fixed values (e.g., 200 in (-1/5)x + 200).
- Operations: Actions like multiplication ((-1/5) × x) or addition (+200).
- Terms: Parts added or subtracted (e.g., (-1/5)x and +200).
- Coefficient: Number multiplying a variable (e.g., -1/5 for x).
- Evaluation: Substituting a value for the variable (e.g., x = 400 gives (-1/5) × 400 + 200 = 120).
Adding and Subtracting Algebraic Terms
Simplifying polynomial expressions involves combining like terms to create equivalent expressions with fewer terms.Like Terms
- Definition: Terms with identical variable parts (same letters and exponents). Example: 3x² and -0.25x²; 4mn and 3nm.
- Unlike Terms: Different variable parts. Example: 3x² and 3x; 4m²n and 3n²m.
Properties:
- Commutative: a + b = b + a; a × b = b × a (allows regrouping).
- Associative: (a + b) + c = a + (b + c); (a × b) × c = a × (b × c) (allows combining).
Simplification Process
Strategy: Group like terms, then add or subtract their coefficients.
Example A: Add 3x² + 5x - 2y + 8 and 5x² + x - 7xy + 4.
- Combine: (3x² + 5x²) + (5x + x) + (-2y) + (-7xy) + (8 + 4) = 8x² + 6x - 2y - 7xy + 12.
- Verify: At x = 2, y = 3, both expressions yield 8.
Example B: Add r² + 3r - 5 and 7r² - 8r - 12.
- Combine: (r² + 7r²) + (3r - 8r) + (-5 - 12) = 8r² - 5r - 17.
- Verify: At r = 2, both yield 5.
Example C: Subtract 6x² + 5x + 4 from 10x² + 8x + 6.
- Rewrite: (10x² + 8x + 6) - (6x² + 5x + 4) = 10x² + 8x + 6 - 6x² - 5x - 4.
- Combine: (10x² - 6x²) + (8x - 5x) + (6 - 4) = 4x² + 3x + 2.
- Verify: At x = 2, both yield 24.
Sign Rules: (-a) × (-b) = +ab; (+a) × (+b) = +ab; (+a) × (-b) = -ab; (-a) × (+b) = -ab.
Multiplication of Polynomials
Multiplication transforms expressions into equivalent forms, often expanding products into sums using the distributive property.Distributive Property
- Definition: a(b + c) = ab + ac. Example: 11 × 12 = (10 + 1)(10 + 2) = 10 × 10 + 10 × 2 + 1 × 10 + 1 × 2 = 132.
- Expansion: Multiplying polynomials to write products as sums.
Monomial × Binomial
Example: 3y(2x - 9y) = 3y × 2x + 3y × (-9y) = 6xy - 27y².
Binomial × Binomial
- General Form: (a + b)(x + y) = ax + ay + bx + by.
- Example: (x + 1)(x + 2) = x(x + 2) + 1(x + 2) = x² + 2x + x + 2 = x² + 3x + 2.
Special Cases:
- (x + y)² = x² + 2xy + y².
- (x - y)² = x² - 2xy + y².
- (x + y)(x - y) = x² - y² (difference of squares).
Binomial × Trinomial
- General Form: (a + b)(x + y + z) = ax + ay + az + bx + by + bz.
- Example: (2x + y)(2a + 3b + c) = 2x(2a + 3b + c) + y(2a + 3b + c) = 4ax + 6bx + 2cx + 2ay + 3by + cy.
Factorise Expressions of the Form ab ± ac
Factorisation writes a sum as a product, the inverse of expansion, by taking out the highest common factor (HCF).HCF Factorisation
Process:
- Identify the HCF of all terms.
- Divide each term by the HCF and write the expression as HCF × (quotient).
Example: 4x³ + 2x² - 6x.
- HCF = 2x.
- Factorise: 2x(2x² + x - 3) = 2x(2x + 3)(x - 1).
Grouping
Process: Group terms with common factors, factor each group, then factor again if possible.
Example: (a - b)x + (b - a)y.
- Rewrite: (b - a) = -(a - b).
- Factorise: (a - b)x - (a - b)y = (a - b)(x - y).
Example: ac + bc + bd + ad.
Group: (ac + bc) + (bd + ad) = c(a + b) + d(a + b) = (a + b)(c + d).
Factorise Expressions of the Form ax² ± bx ± c
Quadratic trinomials (ax² + bx + c) are factorised into two linear binomials, often by trial and error or splitting the middle term.
Trial and Error
Goal: Find m and n such that (x + m)(x + n) = x² + (m + n)x + mn.
Example: x² + 6x + 8.
- Find m, n where mn = 8, m + n = 6: m = 2, n = 4.
- Result: (x + 2)(x + 4).
Cases:
- mn positive, m + n positive: (x + m)(x + n).
- mn positive, m + n negative: (x - m)(x - n).
- mn negative, m + n positive: (x + m)(x - n), m > n.
- mn negative, m + n negative: (x + m)(x - n), m < n.
Splitting the Middle Term
Process: Rewrite bx as mx + nx where m × n = a × c and m + n = b, then group.
Example: x² + 9x + 14 (a = 1, b = 9, c = 14).
- m × n = 1 × 14 = 14, m + n = 9: m = 7, n = 2.
- Rewrite: x² + 7x + 2x + 14 = x(x + 7) + 2(x + 7) = (x + 7)(x + 2).
Example: 3x² + 3x - 6.
- m × n = 3 × (-6) = -18, m + n = 3: m = 6, n = -3.
- Rewrite: 3x² + 6x - 3x - 6 = 3x(x + 2) - 3(x + 2) = (x + 2)(3x - 3) = 3(x + 2)(x - 1).
Non-Unit Coefficients: For a ≠ 1, multiply a and c, find factors, and adjust grouping.
Factorising the Difference of Two Squares
Expressions of the form a² - b² are factorised using a specific identity.
Identity
- Formula: a² - b² = (a + b)(a - b).
- Example: 9x⁴ - 4y² = (3x²)² - (2y)² = (3x² + 2y)(3x² - 2y).
Process:
- Identify a and b (perfect squares).
- Apply the formula.
- Take out HCF first if present (e.g., 18a² - 2b² = 2(9a² - b²) = 2(3a + b)(3a - b)).
Note: Sum of squares (a² + b²) is not factorisable over real numbers.
Factorising: Addition or Subtraction of Two Cubes
Sum and difference of cubes have specific factorisation formulas.
Formulas
- Sum of Cubes: a³ + b³ = (a + b)(a² - ab + b²).
- Difference of Cubes: a³ - b³ = (a - b)(a² + ab + b²).
- Mnemonic (SOAP): For a³ ± b³, the binomial has the Same sign; the trinomial has Opposite sign for ab, Always Positive for b².
Examples
- Difference: 125x³ - 1 = (5x)³ - 1³ = (5x - 1)(25x² + 5x + 1).
- Sum: 27 + p⁶/8 = 3³ + (p²/2)³ = (3 + p²/2)(9 - (3/2)p² + p⁴/4).
Note: The trinomial (a² ± ab + b²) does not factor further over real numbers.
Factorising: Some Mixed Examples
Combines all factorisation techniques, often requiring HCF, difference of squares, cubes, or quadratic trinomials.
Strategy
Steps:
- Take out HCF if present.
- Identify patterns (difference of squares, cubes, quadratic).
- Factor completely, checking by expansion.
Example: 36x² - 49y² = (6x)² - (7y)² = (6x + 7y)(6x - 7y).
Example: 125p¹² + 8x⁶ = (5p⁴)³ + (2x²)³ = (5p⁴ + 2x²)(25p⁸ - 10p⁴x² + 4x⁴).
Simplifying Algebraic Fractions (Quotient Expressions)
Algebraic fractions are simplified by factorising and cancelling common factors.
Key Concepts
- Structure: Numerator (dividend), denominator (divisor), quotient (simplified form).
- Property: ax/a = x if a ≠ 0.
- Excluded Values: Values making the denominator zero (undefined).
Process
- Factorise numerator and denominator.
- Cancel common factors.
- List excluded values.
- Example: (x² + 5x + 6)/(x + 2) = (x + 2)(x + 3)/(x + 2) = x + 3, if x ≠ -2.
Lowest Common Multiples (LCM) and Highest Common Factors (HCF)
LCM and HCF are used for fractions and factorisation.
LCM
- Definition: Product of all variables with their highest exponents.
- Example: For ab, a²bc, ab³: LCM = a²b³c.
- Example: For 2x², 4x³y, 3x⁴y³z: LCM = 12x⁴y³z.
HCF
- Definition: Product of common variables with their lowest exponents.
- Example: For ab, a²bc, ab³: HCF = ab.
- Example: For 2x², 4x³y, 3x⁴y³z: HCF = x².
Adding and Subtracting Algebraic Fractions
Fractions are added or subtracted by finding a common denominator, typically the LCM.
Process
- Find LCM of denominators.
- Rewrite fractions with LCM as denominator.
- Add or subtract numerators, simplify, and list excluded values.
Example: a/(2b) + b/(3a) - (a² + 2b²)/(6ab).
- LCM = 6ab.
- Rewrite: (3a²)/(6ab) + (2b²)/(6ab) - (a² + 2b²)/(6ab) = (3a² + 2b² - (a² + 2b²))/(6ab) = 2a²/(6ab) = a/(3b), if a ≠ 0, b ≠ 0.
Simplification: Factorise and cancel after combining.
Multiplying Algebraic Fractions
Multiplication involves multiplying numerators and denominators, often requiring factorisation.
Property: (a/b) × (x/y) = (ax)/(by), if b ≠ 0, y ≠ 0.
Process
- Factorise where needed.
- Multiply and simplify, listing excluded values.
Example: (x² - x - 2)/(x² + x - 6) × (x² + 3x)/(x² + 3x + 2).
- Factorise: [(x + 1)(x - 2)]/[(x + 3)(x - 2)] × [x(x + 3)]/[(x + 1)(x + 2)].
- Simplify: x/(x + 2), if x ≠ 2, -3, -1, -2.
Dividing Algebraic Fractions
Division uses the multiplicative inverse (reciprocal).
Property: (a/b) ÷ (x/y) = (a/b) × (y/x) = ay/(bx), if b ≠ 0, x ≠ 0, y ≠ 0.
Process
- Take reciprocal of the second fraction, then multiply.
- Factorise, simplify, and list excluded values.
Example: (x² - x - 2)/(x² + x - 6) ÷ (x² + 3x + 2)/(x² + 3x).
- Rewrite: [(x + 1)(x - 2)]/[(x + 3)(x - 2)] × [x(x + 3)]/[(x + 1)(x + 2)].
- Simplify: x/(x + 2), if x ≠ 2, -3, -1, 0.
Points to Remember
- Mathematical notation uses symbols for precise communication.
- Constants are fixed; variables change; operations combine them.
- Evaluating an expression means substituting values for variables.
- Equivalent expressions yield the same value for the same input.
- Sum expressions involve addition/subtraction as the last step; product expressions involve multiplication; quotient expressions involve division.
- Polynomials have multiple terms: monomial (1 term), binomial (2 terms), trinomial (3 terms).
- Like terms have identical variable parts and are combined using commutative and associative properties.
- Expansion uses the distributive property; factorisation is its inverse.
- Difference of squares: a² - b² = (a + b)(a - b).
- Sum/difference of cubes: a³ + b³ = (a + b)(a² - ab + b²); a³ - b³ = (a - b)(a² + ab + b²).
- Algebraic fractions require factorisation to simplify, with excluded values where the denominator is zero.
Difficult Words
- Constant: A fixed value in an expression (e.g., 200 in (-1/5)x + 200).
- Variable: A symbol representing a changing value (e.g., x for price).
- Operation: Mathematical action like addition or multiplication.
- Term: A part of an expression added or subtracted (e.g., (-1/5)x).
- Coefficient: Number multiplying a variable (e.g., -1/5 in (-1/5)x).
- Polynomial: Expression with multiple terms (e.g., x² + 5x + 6).
- Factorisation: Writing a sum as a product (e.g., x² + 5x + 6 = (x + 2)(x + 3)).
- HCF: Highest common factor, the largest common factor of terms.
- LCM: Lowest common multiple, used for common denominators.
- Quotient: Result of division (e.g., x + 3 in (x² + 5x + 6)/(x + 2)).
- Excluded Values: Values making a denominator zero, rendering a fraction undefined.
Summary
The Algebraic Expressions chapter for Grade 10 Technical Mathematics covers manipulating polynomials and algebraic fractions. Students learn to represent sets using number lines, interval notation, and set builder notation, and model real-world scenarios (e.g., sales) with expressions. Key skills include adding/subtracting like terms, multiplying polynomials (monomial × binomial, binomial × binomial/trinomial), and factorising using HCF, grouping, quadratic trinomials, difference of squares, and sum/difference of cubes. Algebraic fractions are simplified, added, subtracted, multiplied, and divided using factorisation and LCM, with attention to excluded values. These skills are vital for technical applications like engineering and physics.|
1 videos|57 docs|4 tests
|
FAQs on Algebraic Expressions Chapter Notes - Mathematics for Grade 10
| 1. What are the basic rules for adding and subtracting algebraic terms? |  |
| 2. How do you multiply polynomials? |  |
| 3. What is the difference of two squares and how do you factor it? |  |
| 4. How do you factor expressions in the form ax² ± bx ± c? |  |
| 5. What is simplifying algebraic fractions and how is it done? |  |
















