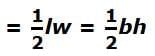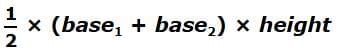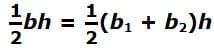Area Chapter Notes | Mathematics for Grade 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Parallelograms |

|
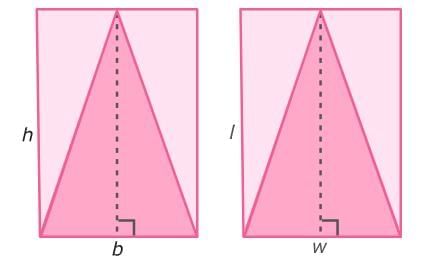
| Triangle |

|
| Trapezoids |

|
| Coordinate Plane |

|
Introduction
Parallelograms, triangles, and trapezoids are shapes with unique properties. A parallelogram has two pairs of parallel sides, including special types like rectangles and squares. Triangles are classified by sides (equilateral, isosceles, scalene) or angles (acute, right, obtuse), and their area is half the base times height. Trapezoids have one pair of parallel sides, with area calculated using both bases and height. The coordinate plane, a grid with x- and y-axes, helps plot points using ordered pairs. This guide simplifies these concepts with clear examples.
Parallelograms
What is a parallelogram?
A parallelogram is a quadrilateral with two pairs of parallel sides.

There are some special types of parallelograms:
- A rectangle is a parallelogram with four right angles.
- A rhombus is a parallelogram with four equal sides.
- A square is a parallelogram with four right angles and four equal sides.

Area of a parallelogram
Area formula
The formula for the area of a parallelogram is base times height:
Area = base × height
For Example: The base of this parallelogram is 6 units. The height of this parallelogram is 8 units.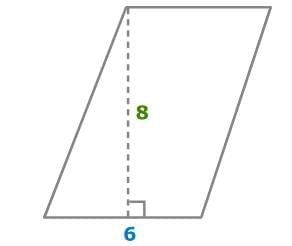 A = 6 x 8
A = 6 x 8
A = 48
So, the area of the parallelogram is 48 square units.
Why does this work?
To understand why this formula works, turn the parallelogram into a rectangle.
First, cut the parallelogram into two pieces.

Then, rearrange the pieces to form a rectangle.
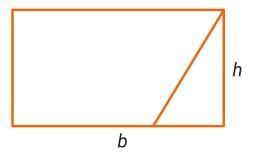
To find the area of a rectangle, you multiply its length by its width. In a parallelogram, the base is the same as the rectangle’s length, and the height is the same as the rectangle’s width. So, multiplying the base by the height gives the same result as multiplying the length by the width.
Area of rectangle = lw = bh
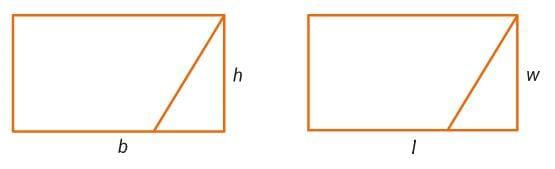
Since any parallelogram can be cut and rearranged to form a rectangle, you use the same formula to find the area of both shapes.
Perimeter of a parallelogram
To find the perimeter of any shape, you add up the lengths of all its sides. A parallelogram has two pairs of equal sides, so you can find its perimeter by doubling the length and width, then adding the two results together.
Perimeter = (2 × base) + (2 × side)
For Example: The base of this parallelogram is 6 units. The side of this parallelogram is 5 units. Plug those numbers into the equation.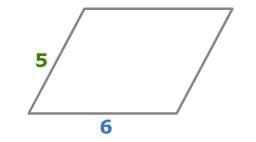
P = (2 × 6) + (2 × 5)
P = 12 + 10
P = 22
So, the perimeter of the parallelogram is 22 units!
Triangle
Area of triangles
Area formula
The formula for the area of a triangle is 1/2 times the base times the height.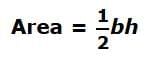 For Example: The base of this triangle is 12 units. The height of this triangle is 4 units.
For Example: The base of this triangle is 12 units. The height of this triangle is 4 units.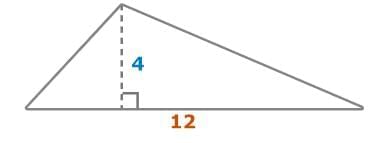 A = 1/2 x 12 x 4
A = 1/2 x 12 x 4
A = 6 x 4
A = 24
So, the area of the triangle is 24 square units.
Why does this work?
To understand why this formula works, turn the triangle into a rectangle.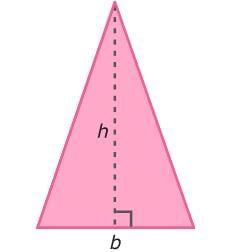 First, make a copy of the triangle.
First, make a copy of the triangle. Then, cut the copy into pieces.
Then, cut the copy into pieces.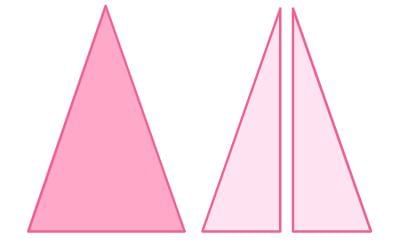 Next, rearrange the pieces to form a rectangle.
Next, rearrange the pieces to form a rectangle.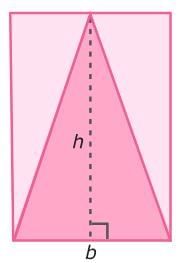 The area of a rectangle is found by multiplying its length by its width. In a triangle, the base matches the rectangle’s length, and the height matches the rectangle’s width. So, multiplying the length by the width is the same as multiplying the base by the height.
The area of a rectangle is found by multiplying its length by its width. In a triangle, the base matches the rectangle’s length, and the height matches the rectangle’s width. So, multiplying the length by the width is the same as multiplying the base by the height.
Area of rectangle = lw = bh
Since the rectangle is made up of two copies of the same triangle, the area of the triangle is 1/2 of the area of the rectangle!
Area of triangle
Types of triangles
Triangles have special names based on their side lengths and angle measures.
Classifying triangles by side length
When you classify triangles by their side lengths, you use the words equilateral, isosceles, and scalene.
Let's find out what those words mean!
An equilateral triangle has three equal sides. This is an example of an equilateral triangle.
An isosceles triangle has two equal sides. This is an example of an isosceles triangle.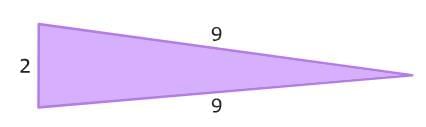 A scalene triangle has no equal sides. This is an example of a scalene triangle.
A scalene triangle has no equal sides. This is an example of a scalene triangle.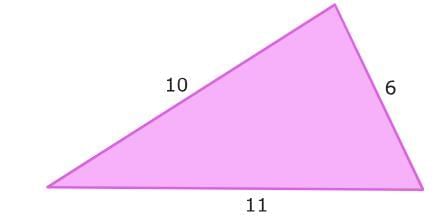
Classifying triangles by angle measure
When you classify triangles by their angle measures, you use the words acute, right, and obtuse.
Let's find out what those words mean!
An acute triangle has three acute angles. Acute angles measure less than 90°. This is an example of an acute triangle.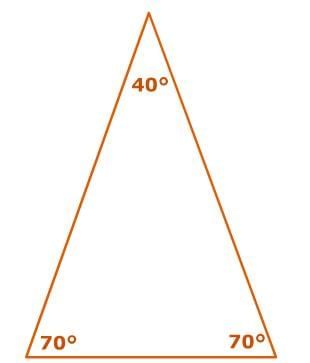 A right triangle has one right angle. Right angles measure exactly 90°. This is an example of a right triangle.
A right triangle has one right angle. Right angles measure exactly 90°. This is an example of a right triangle.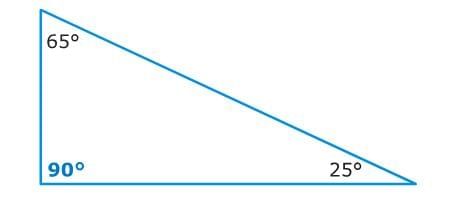 An obtuse triangle has one obtuse angle. Obtuse angles measure more than 90°. This is an example of an obtuse triangle.
An obtuse triangle has one obtuse angle. Obtuse angles measure more than 90°. This is an example of an obtuse triangle.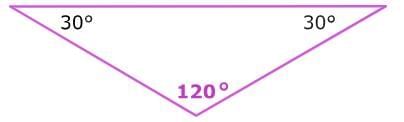
Classifying triangles two ways
This is a right isosceles triangle. It has a right angle and two equal sides.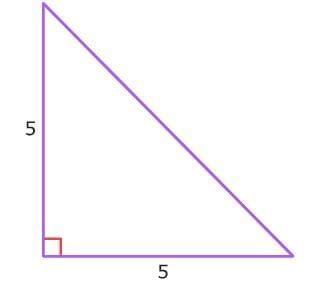
Trapezoids
What is a trapezoid?
A trapezoid is a quadrilateral with exactly one pair of parallel sides.
 Outside the United States and Canada, this shape is called a trapezium.
Outside the United States and Canada, this shape is called a trapezium.
Did you know?
Not everyone agrees on what a trapezoid is! Some people define a trapezoid as having at least one pair of parallel sides, rather than exactly one pair. With that definition, even a parallelogram would be considered a type of trapezoid.
Area of a trapezoid
The formula for the area of a trapezoid is 1/2 the sum of the two bases times the height.
Area =
For Example: The bases of this trapezoid are 6 units and 10 units. The height of this trapezoid is 7 units.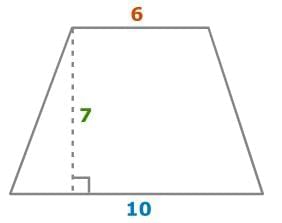
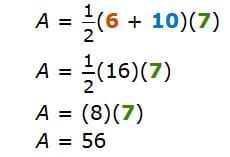
So, the area of the trapezoid is 56 square units.
Why does this work?
To understand why this formula works, turn the trapezoid into a parallelogram.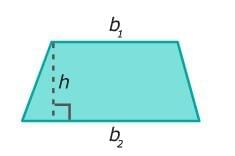 First, make a copy of the trapezoid.
First, make a copy of the trapezoid. Flip the second trapezoid. Then, rearrange the two trapezoids to form a parallelogram.
Flip the second trapezoid. Then, rearrange the two trapezoids to form a parallelogram. You can find the area of a parallelogram by multiplying the base times the height. The base of the parallelogram is equal to b1 + b2. So, plug b1 + b2 into the formula.
You can find the area of a parallelogram by multiplying the base times the height. The base of the parallelogram is equal to b1 + b2. So, plug b1 + b2 into the formula.
Area of parallelogram = bh = (b1 + b2)h
 Since the parallelogram is made up of two copies of the same trapezoid, the area of the trapezoid is 1/2 of the area of the parallelogram!
Since the parallelogram is made up of two copies of the same trapezoid, the area of the trapezoid is 1/2 of the area of the parallelogram!
Area of trapezoid =
Coordinate Plane
A coordinate plane is a grid formed by two number lines. The horizontal number line is called the x-axis. The vertical number line is called the y-axis. The two axes meet at the origin. The origin is at zero on both number lines.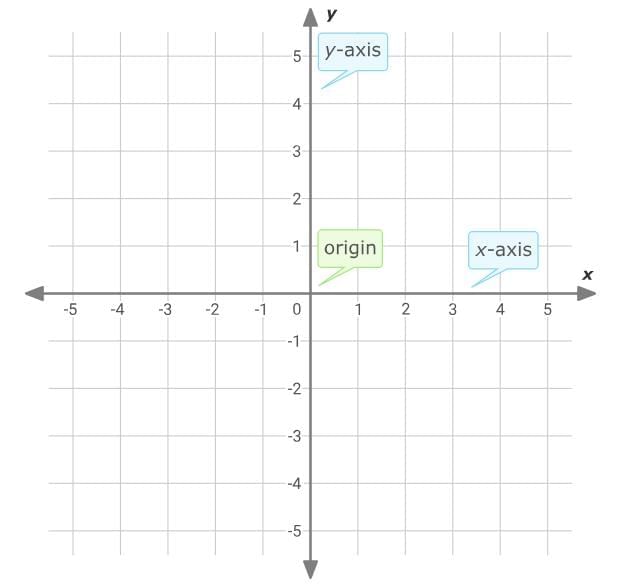 The axes divide the coordinate plane into four quadrants. The quadrants are named using Roman numerals.
The axes divide the coordinate plane into four quadrants. The quadrants are named using Roman numerals.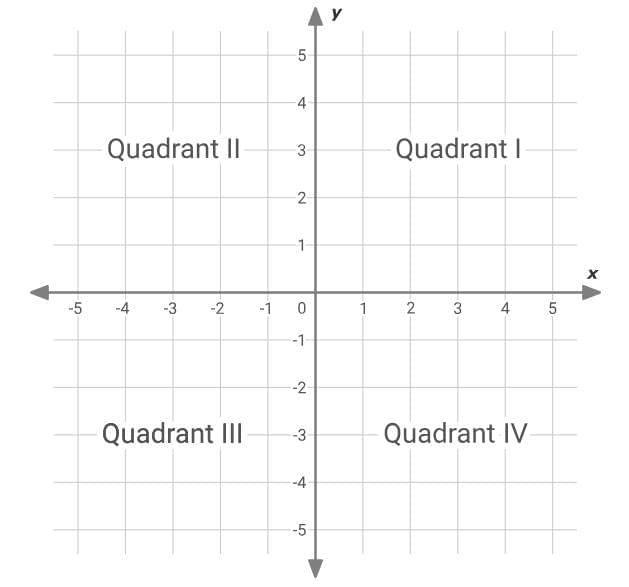
How do you plot a point on the coordinate plane?
- Each location on the coordinate plane is represented by an ordered pair. An ordered pair has two numbers written in the form (x,y). The first number is the x-coordinate. It tells you the location of the point on the x-axis. The second number is the y-coordinate. It tells you the location of the point on the y-axis.
- To plot a point on the coordinate plane, follow these steps:
- Start at the origin.
- Move left or right to find the x-coordinate on the x-axis.
- Move up or down to find the y-coordinate on the y-axis. Plot a point at this location.
- For Example: Let's try it for (4, 2).
Start at the origin.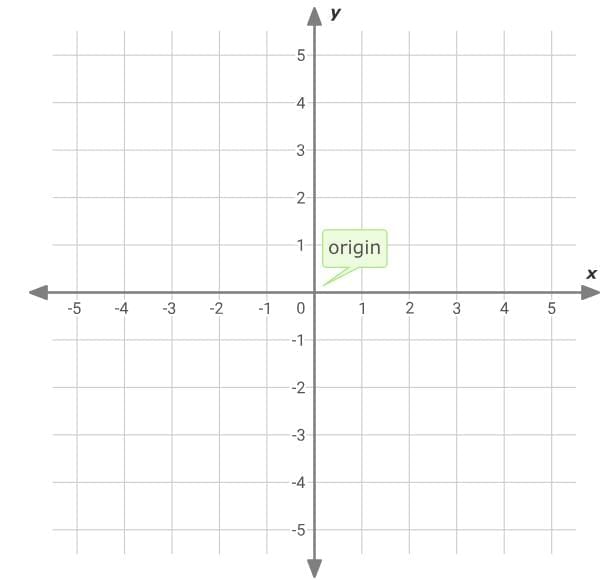 Then, find the x-coordinate on the x-axis. Since the x-coordinate in (4, 2) is 4, move to the right 4 spaces.
Then, find the x-coordinate on the x-axis. Since the x-coordinate in (4, 2) is 4, move to the right 4 spaces.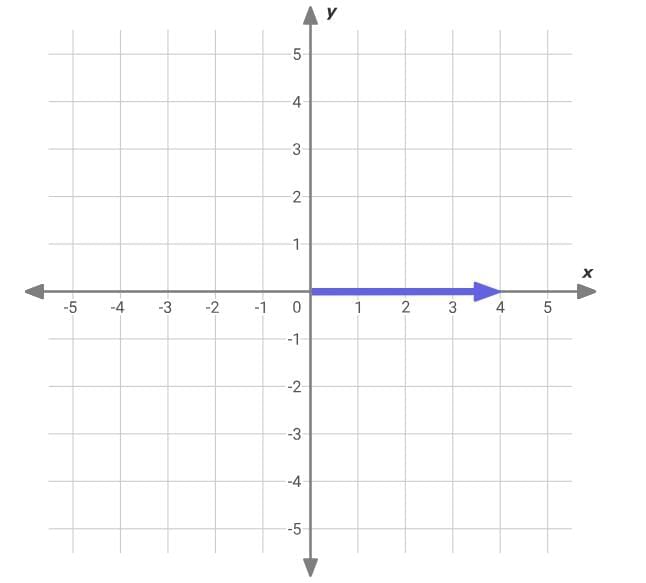 Now, find the y-coordinate on the y-axis. Since the y-coordinate in (4, 2) is 2, move up 2 spaces. Plot a point at this location.
Now, find the y-coordinate on the y-axis. Since the y-coordinate in (4, 2) is 2, move up 2 spaces. Plot a point at this location.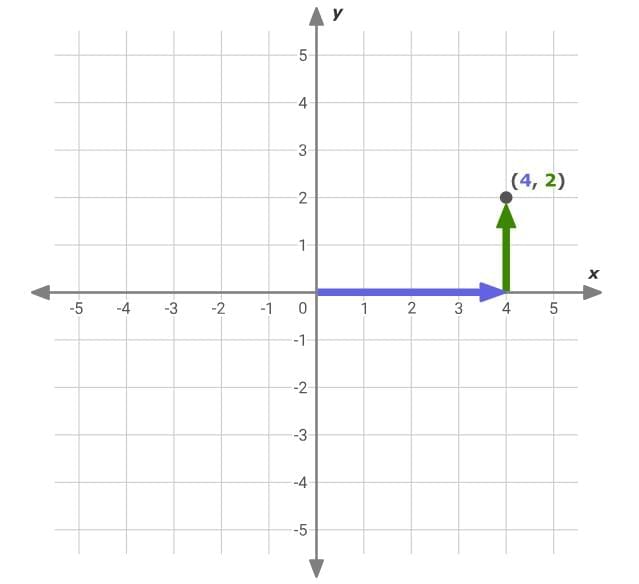
|
36 videos|63 docs|14 tests
|
FAQs on Area Chapter Notes - Mathematics for Grade 6
| 1. What is a parallelogram and how do you calculate its area? |  |
| 2. How can you find the area of a triangle? |  |
| 3. What is the formula for calculating the area of a trapezoid? |  |
| 4. How do you plot points on a coordinate plane? |  |
| 5. Why is understanding area important in real life? |  |