Arithmetic Progression Chapter Notes | Elementary Mathematics for PAT PDF Download
| Table of contents |

|
| Introduction |

|
| Arithmetic Progressions |

|
| nth term of an AP |

|
| Sum of first n terms of an AP |

|
Introduction
Patterns can be observed in our daily lives, even in something as simple as a savings account. For example, if we start with Rs. 2000 and add Rs. 500 each month, the balance follows a predictable pattern: Rs. 2000, Rs. 2500, Rs. 3000, and so on. This is called an Arithmetic progression (AP).
Arithmetic Progressions
Arithmetic Progressions (APs) are sequences of numbers in which the difference between consecutive terms remains constant. This constant difference is called the common difference. In an arithmetic progression, each term can be obtained by adding the common difference to the previous term.
Here is a list of numbers, observe the pattern of the numbers.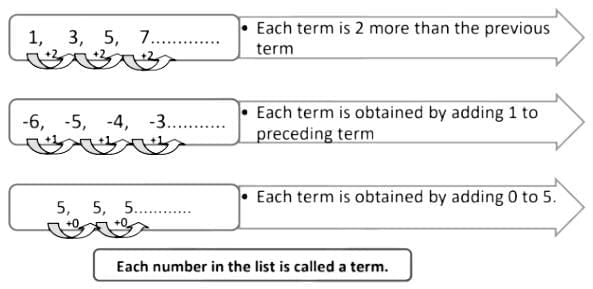
- Here, we see that each successive term is obtained by adding a fixed number to the preceding term except the first term. Such a list of numbers is said to be in arithmetic progression.
- This fixed number is called the common difference of the AP. This number can be positive, negative, or zero.
- Let us denote the first term of an AP by a1, the second term by a2,.........nth term by an and the common difference by d. Then the AP becomes a1, a2, a3, ... ... ... ... ... aₙ.
So, a1 − a2 = a3 − a2 =.........= an − an−1 = d
Arithmetic Progressions (APs) can be categorized as either finite or infinite based on the number of terms they contain.
- Finite Arithmetic Progression: A finite Arithmetic Progression (AP) refers to a sequence of numbers that has a specific and limited number of terms. The progression stops after a certain term, and there is a finite number of terms in the sequence.
Example: 229, 329, 429, 529, 629 - Infinite Arithmetic Progression: In contrast, an infinite Arithmetic Progression (AP) is a sequence of numbers that continues indefinitely without an endpoint. It goes on infinitely, and there is no fixed limit on the number of terms.
Example: 2, 4, 6, 8, 10, 12, 14, 16, 18…..…
Understanding the distinction between finite and infinite APs helps us analyze different types of sequences and apply appropriate methods and formulas accordingly.
Solved Examples
Example 1: In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?
a) The cost of digging a well after every meter of digging when it costs Rs. 150 for the first meter and rises by Rs. 50 for each subsequent meter.
Sol:
Cost of digging the first meter = Rs.150
Cost of digging second metre = Rs.(150 + 50) = Rs.200
Cost of digging third metre = Rs.(150 + 2× 50) = Rs. 250
In this case, each term is obtained by adding Rs. 50 to the preceding term. Hence, they make an AP.
b) The amount of water present in a cylinder when a vacuum pump removes 1⁄4 of the air remaining in the cylinder at a time.
Sol:
Let the amount of air present in the cylinder be x units.
According to the question,
Amount of air left in the cylinder after using vacuum pump first time= y - y4 = 3y4
Amount of air left in the cylinder after using vacuum pump the second time=
3y4 -( 14 × 3y4) = 3y4 - 3y16 = 12y - 3y16 = 9y4
List of numbers y, 3y4, 9y4, ...
a2 - a1: 3y4 - y = -y4
a3 - a2: 9y4 - 3y4 = 3y4
As the common difference of the terms is not the same, they do not form AP.
Example 2: Find the common difference of the AP
1p, 1 - 2pp, 1 - 4pp, ...
Sol:
Common difference (d) = Second Term – First Term
d = 1 - 2pp - 1p
d = 1 - 2p - 1p = -2pp = -2
Therefore, common difference = -2
Example 3: For what value of k will k + 10 , 2k, and 2k + 8 are the consecutive terms of an AP.
Sol:
If k + 10 , 2k, and 2k + 8 are in AP then,
a1 = k + 10 , a2 = 2k and a3 = 2k + 8
Common Difference (d)
d = a2 - a1 = a3 - a2
2k - (k + 10) = 2k + 8 - (2k)
k - 10 = 8
k = 18
nth term of an AP
Let a1 , a2, a3, ... ... ... ... ... an be an AP whose first term a1 is a and the common difference is d.Then,
The nth term an of the AP with the first term a and common difference d is given by
an = a + (n − 1)d
Solved Examples
Example 5: Find the 25th term of the AP: -5, -5/2, 0, 5/2
Sol:
Here, a = −5
Common Difference (d) = a2 − a1
= -52 - (-5) = -52 - (-5)1 = -5 + 102 = 52
We know, an = a + (n − 1)d
25th term, a25
= -5 + (25 - 1) × 52
⇒ -5 + 24 × 52
= -5 + 60 = 55
25th term of the given AP is 55.
Example 6: For an AP, if a18 − a14 = 36, then find the common difference d.
Sol:
We know, an = a + (n − 1)d
a18 = a + (18 − 1)d = a + 17d
a14 = a + (14 − 1)d = a + 13d
a18 − a14 = 36
a + 17d − (a + 13d) ⇒ a + 17d − a − 13d
4d = 36
d = 9
Therefore, the common difference (d) = 9
Example 7: If an = 6 − 11n, then find the common difference.
Sol:
Given: an = 6 − 11n ............... (1)
Replacing n by n+1 in eq (1) we get
a(n+1) = 6 – 11(n+1)
a(n+1) = 6 – 11n-11
a(n+1) = - 11n – 5
Common difference, d = a(n+1) – an
d= -11n-5 – (6-11n)
d = -11
Example 8: Find the 7th term of the sequence whose nth term is given by an = (−1)n−1. n2
Sol:
Given: an = (−1)n−1. n2
The 7th term of the sequence, a7 = (−1)7−1. 72
= (−1)6. 72 = 49
Example 9: An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.
Sol:
Let a be the first term and d be the common difference of the given AP.
Given: a3 = 12 and a50 = 106
We know, an = a + (n − 1)d
a3 = a + (3 − 1)d ⇒ a3 = a + 2d
a3 = a + 2d = 12→Eq 1
a50 = a + (50 − 1)d ⇒ a50 = a + 49d
a50 = a + 49d = 106→Eq 2
Subtracting Eq 1 from Eq 2
a + 49d − (a + 2d) = 106 − 12
a + 49d − a − 2d = 94
47d = 94 ⇒ d = 2
Putting the value of d in Eq 1 we get,
a + 2 × 2 = 12
a = 12 − 4 = 8
29th term, a29 = a + 28d = 8 + 28 × 2 = 8 + 56 = 64
Example 10: Find how many two-digit numbers are divisible by 7.
Sol:
Two-digit numbers are 10, 11, 12, 13, ..................97, 98, 99, 100.
Here 14, 21, 28...................... 91, 98 are divisible by 7.
This list of numbers forms an AP, where a = 14 and
d = 21 − 14 = 7
Let the number of terms be n, then an = 98
98 = 14 + (n − 1)7 ⇒ 98 = 14 + 7n − 7
7n + 7 = 98 ⇒ 7n = 98 − 7
7n = 91
n = 13
Hence, 13 two-digit numbers are divisible by 7.
Sum of first n terms of an AP
- One of the most important aspects of AP is finding the sum of its terms. The sum of the first n terms of an AP is a commonly used formula in mathematics. It allows us to quickly find the total sum of a given number of terms in an AP without having to add each term individually.
- The sum of first n terms of an AP is given by
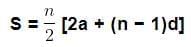
- Now, this can also be written as

- We know an = a + (n − 1)d

- If the number of terms in the AP is n then, an is the last term and an = I
therefore,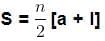
- This form of the result is useful when only the first and the last term are given and the common difference is not given.
Example 11: If the nth term of an AP is (2n + 2), find the sum of first n terms of the AP.
We have,
an = 2n + 2 ⇒ a1 = 2 × 1 + 2 = 4
Therefore, a1 = a is the first term and an = l is the last term of the AP.
As we know the first and the last term of the AP, the sum of n terms is given by,S = n2 [a + l]
S = n2 [4 + 2n + 2]
S = n2 [2n + 6] = 2n2 [n + 3] = n[n + 3]
Sum of first n terms of the given AP is n[n + 3]
Example 12: Find the sum of the first 25 terms of an AP, whose nth term is given by an = 6 − 3n.
Given: an = 6 − 3n
a1 = 6 − 3 × 1 = 3a25 = 6 − 3 × 25 = −69
Therefore, a1 = a = 3 is the first term and a25 = −69S = n2 [a + l]
S = 252 [3 + (-69)] = 252 [3 - 69] = 252 [-66]
S = 25 × (-33) = -825
Therefore, the sum of the first 25 terms of the given AP is -825.
Example 13: Find the sum of all two-digit odd positive numbers.
Two-digit odd positive numbers are 11, 13, 15..................99 which form an AP.
Here, First term a = 11, last term (l) = 99 and common difference (d) = 13 – 11 = 2
Now we have to find the number of terms.We know, l = an = a + (n − 1)d
99 = 11 + (n − 1) × 2
99 = 11 + 2n − 2 ⇒ 99 = 9 + 2n
99 − 9 = 2n ⇒ 90 = 2n
n = 45S = n2 [a + l]
S = 452 [11 + 99] = 452 [110] = 45 × 55 = 2475
Therefore, the sum of all two-digit odd positive numbers is 2475.
|
7 videos|256 docs|37 tests
|
FAQs on Arithmetic Progression Chapter Notes - Elementary Mathematics for PAT
| 1. What is an arithmetic progression (AP) and how is it defined? |  |
| 2. How do you find the nth term of an arithmetic progression? |  |
| 3. What is the formula for the sum of the first n terms of an arithmetic progression? |  |
| 4. Can you provide an example of an arithmetic progression and compute its nth term and sum? |  |
| 5. Why is understanding arithmetic progressions important in mathematics? |  |















