Circle Chapter Notes | Mathematics Class 6 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Circle |

|
| Parts of a Circle |

|
| Construction of Circles |

|
Introduction
Imagine drawing a perfect round shape, like the sun or a coin, where every point on the edge is equally far from one special point in the middle. That’s a circle! Circles are fascinating because they are simple yet appear everywhere—in wheels, clocks, and even pizza! This chapter will take you on a journey to understand the different parts of a circle, how they work together, and how to draw them using a compass and ruler. Get ready to explore this beautiful shape step by step!
Circle
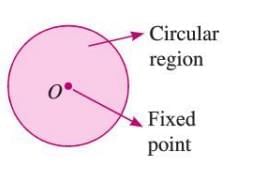
- A circle is a round shape where all points on the edge are at the same distance from a fixed point called the center.
- The area inside the circle is called the circular region.
- It is a closed curve formed in a plane.
- Example: In a figure, point O is the center, and the shaded area inside the circle is the circular region.
Parts of a Circle
Centre
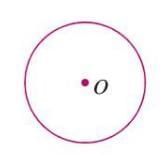
- The center is the fixed point inside the circle from which all points on the edge are equally distant.
- It is the heart of the circle, defining its position.
- Example: In a figure, point O is the center of the circle.
Radius
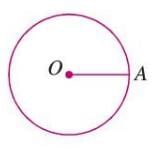
- The radius is the distance from the center to any point on the circle’s edge.
- It is the fixed length that defines the size of the circle.
- Example: In a figure, line segment OA is a radius of the circle.
- Solved Example: If the radius of a circle is 4 cm, the distance from the center O to point P on the circle is 4 cm.
Chord
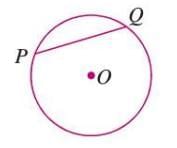
- A chord is a line segment that connects any two points on the circle’s edge.
- It lies completely inside the circle.
- Example: In a figure, line segment PQ is a chord of the circle.
- Solved Example: If points A and B lie on a circle and are joined by a line segment AB, then AB is a chord.
Segment
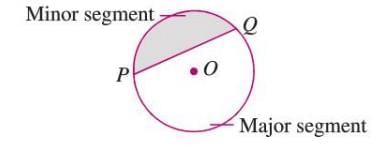
- A chord divides the circle into two parts, each called a segment.
- The larger part (more than half the circle) is the major segment.
- The smaller part (less than half the circle) is the minor segment.
- The major segment includes the center of the circle.
- Points to Remember:
- The major segment contains the center.
- A diameter splits the circle into two equal segments.
- A quarter of a circle, bounded by two perpendicular radii, is called a quadrant.
Diameter
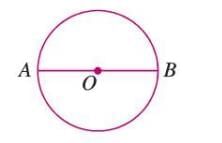
- The diameter is a special chord that passes through the center of the circle.
- It is the longest chord in a circle.
- Formula: Diameter = 2 × Radius
- It divides the circle into two equal parts, each called a semicircle.
- Example: In a figure, line segment AB is a diameter passing through the center O.
- Solved Example: If the radius of a circle is 6 cm, the diameter is 2 × 6 = 12 cm.
Circumference
- The circumference is the total length of the circle’s boundary.
- It represents the distance around the circle.
- Example: In a figure, PQR is the circumference of the circle.
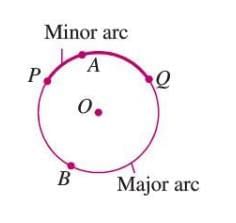
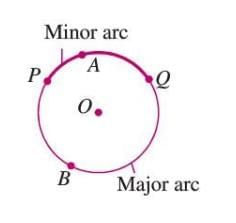
Arc
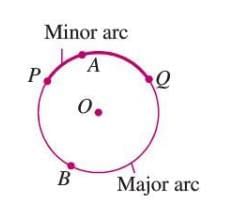
- An arc is a portion of the circumference between two points on the circle.
- If the arc is longer than half the circumference, it is a major arc.
- If the arc is shorter than half the circumference, it is a minor arc.
- Example: In a figure, arc PAQ is a minor arc, and arc PBQ is a major arc.
Sector
- A sector is the region enclosed by two radii and an arc of the circle.
- A minor sector is formed by a minor arc and two radii.
- A major sector is formed by a major arc and two radii.
- Example: In a figure, OAPB is a minor sector formed by minor arc APB and radii OA and OB. OAQB is a major sector formed by major arc AQB and radii OA and OB.
Interior and Exterior
- The interior of a circle is the set of all points inside the circle.
- The exterior of a circle is the set of all points outside the circle.
- Example: In a figure, points O, A, B, and P are inside the circle (interior), while points C, Q, and D are outside (exterior).
- Solved Example: If the radius of a circle is 5 cm and a point P is 4 cm from the center, P lies in the interior. If a point Q is 6 cm from the center, Q lies in the exterior.
Secant
- A secant is a straight line that intersects the circle at two distinct points.
- It crosses through the circle, touching it at two places.
- Example: In a figure, line AB is a secant intersecting the circle at points C and D.
Tangent
- A tangent is a straight line that touches the circle at exactly one point.
- The point where the tangent touches the circle is called the point of contact.
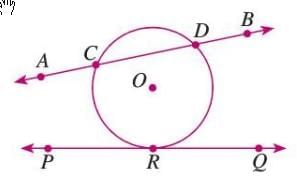
Example: In a figure, line PQ is a tangent touching the circle at point R, the point of contact.
Points to Remember:
- A circle has only one center but can have infinite radii, chords, and diameters.
Construction of Circles
To Construct a Circle of Given Radius
- Measure the desired radius using a compass and ruler.
- Mark the center point on the paper.
- Place the compass’s pointed end at the center.
- Rotate the compass to draw the circle.
Example:To draw a circle with center O and radius 5 cm: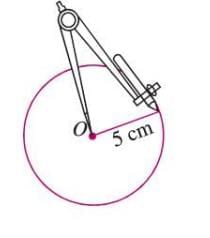
- Step 1: Use a ruler to set the compass to 5 cm.
- Step 2: Mark point O as the center.
- Step 3: Place the compass point at O.
- Step 4: Rotate the compass to draw the circle.
To Construct a Circle with Given Line Segment as a Diameter
- Find the midpoint of the line segment by drawing its perpendicular bisector.
- Use the midpoint as the center and half the line segment’s length as the radius.
- Draw the circle using a compass.
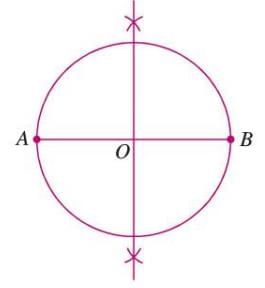
Example: To draw a circle with line segment AB of length 8 cm as the diameter:
- Step 1: Draw the perpendicular bisector of AB, intersecting at point O.
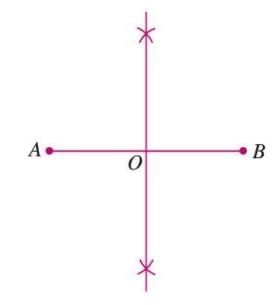
- Step 2: Use point O as the center and draw a circle with radius AO or OB (4 cm).
To Construct a Circle Passing Through Three Non-Collinear Points
- Join two pairs of the three points to form two chords.
- Draw perpendicular bisectors of these chords; their intersection is the center.
- Use the distance from the center to any of the three points as the radius.
- Draw the circle using a compass.
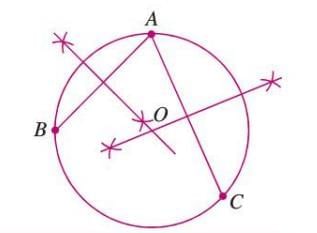
Example: To draw a circle passing through points A, B, and C:
- Step 1: Join AB and AC, then draw their perpendicular bisectors, intersecting at point O.
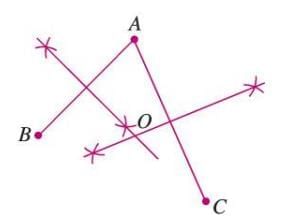
- Step 2: Draw a circle with center O and radius OA, OB, or OC.
|
44 videos|202 docs|24 tests
|
FAQs on Circle Chapter Notes - Mathematics Class 6 ICSE
| 1. What is a circle and what are its basic properties? |  |
| 2. What are the different parts of a circle? |  |
| 3. How do you construct a circle using a compass? |  |
| 4. What is the formula to find the circumference and area of a circle? |  |
| 5. Why are circles important in mathematics and real-world applications? |  |




















