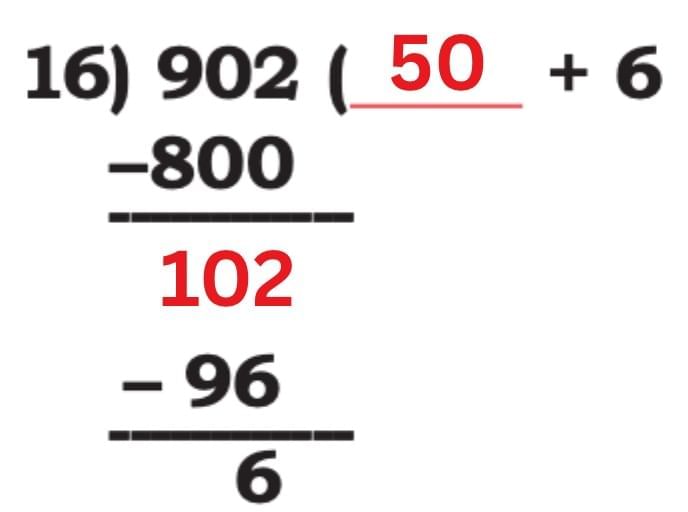Class 5 Exam > Class 5 Notes > Mathematics (Maths Mela) Class 5 - New NCERT > Chapter Notes: Coconut Farm
Coconut Farm Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
Welcome to Susie and Sunitha’s coconut farm, where coconuts make math fun. They arrange coconuts in rows to learn multiplication, share them equally to understand division, and pack them into bags to see multiplication as repeated addition. When coconuts don’t divide evenly, they discover remainders. The farm becomes their classroom, turning everyday work into exciting math practice.
What is Multiplication?
- Multiplication is a quick way to add the same number many times.
- It helps us find the total when we have equal groups.
- We use the sign “×” (times) for multiplication. The numbers we multiply are called factors, and the answer is the product.
- We use multiplication in daily life—like counting apples in baskets, chairs in rows, or boxes in a stack.
- For example, if there are 4 baskets and each basket has 2 apples, we can multiply 2 × 4 = 8 to find the total apples, instead of adding 2 + 2 + 2 + 2.
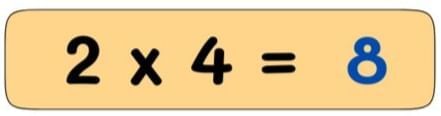
What is Division?
- Division is a way to split a number into equal parts or groups.
- It’s like sharing something so everyone gets the same amount.
- We use the sign “÷” (divide) or “/” for division. The number we divide is called the dividend, the number we divide by is the divisor, and the answer is the quotient.
- We use division in daily life - like sharing chocolates, splitting money, or making equal teams.
- For example, if there are 122 apples and 5 friends, we can divide 122 ÷ 5 = 24 to find that each friend gets 24 apples and 2 are left.

Q: Observe the following array of coconuts. Write two division facts using the given multiplication fact.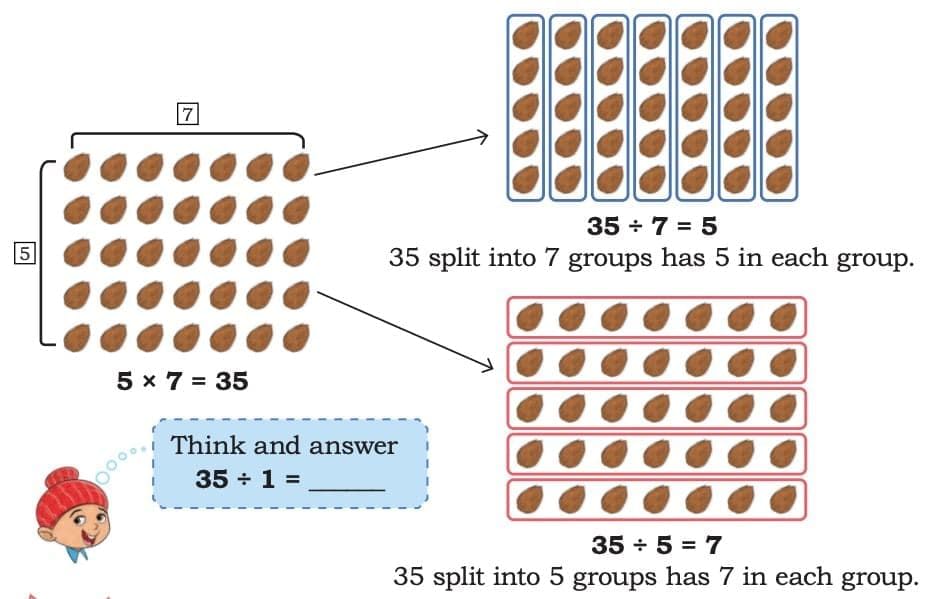
Sol: From the given multiplication fact 5 × 7 = 35, the two division facts are:
- 35 ÷ 7 = 5 → 35 split into 7 groups has 5 in each group.
- 35 ÷ 5 = 7 → 35 split into 5 groups has 7 in each group.
Example: Write the appropriate multiplication fact for the array shown below. Write two division facts that follow from the multiplication fact.

Sol:
In the picture, we see 4 rows of objects.
Each row has 8 objects.
To find the total number of objects, we multiply:
4 × 8 = 32
So, there are 32 objects in all.Now, using this multiplication fact, we can also write two division facts:
If we divide the total objects (32) into groups of 8, we get 32 ÷ 8 = 4 (which means 4 rows).
If we divide the total objects (32) into groups of 4, we get 32 ÷ 4 = 8 (which means 8 objects in each row).
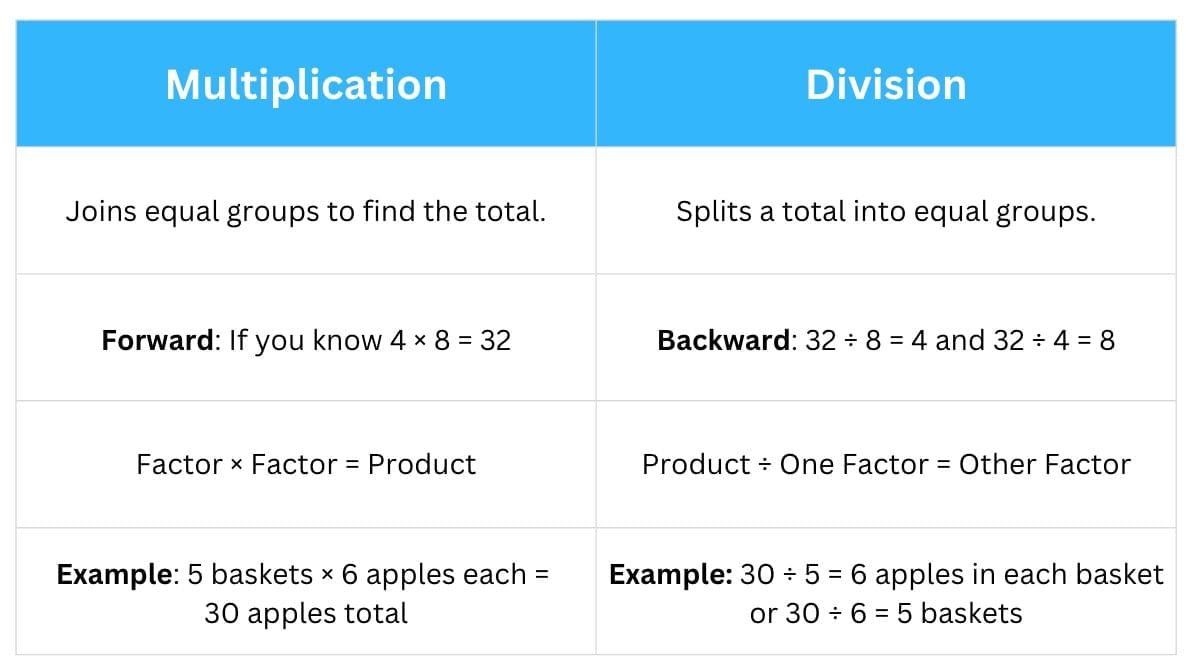
Connection between Multiplication and Division
- Multiplication and division are related.
- In Multiplication, we have two numbers (factors) that make a product.
- In Division, we take the product and divide it by one factor to find the other.
Patterns in Division
- When we divide by 10, 100, 1000, or multiples of these, a clear pattern appears in the answers.
- 10 → answer is 10 times smaller.
- 100 → answer is 100 times smaller.
- 1000 → answer is 1000 times smaller.
- In whole numbers, if the number ends with the same number of zeros as the divisor, those zeros can be removed.
Finding the Patterns in Division:

Sol:
1000 ÷ 10 = 100 because 10 × 100 = 1000.
2000 ÷ 2 = 1000 because 2 × 1000 = 2000.
3300 ÷ 3 = 1100 because 3 × 1100 = 3300.
1000 ÷ 100 = 10 because 100 × 10 = 1000.
2000 ÷ 20 = 100 because 20 × 100 = 2000.
3300 ÷ 300 = 11 because 300 × 11 = 3300.
1600 ÷ 4 = 400 because 4 × 400 = 1600.
3700 ÷ 37 = 100 because 37 × 100 = 3700.
4000 ÷ 40 = 100 because 40 × 100 = 4000.
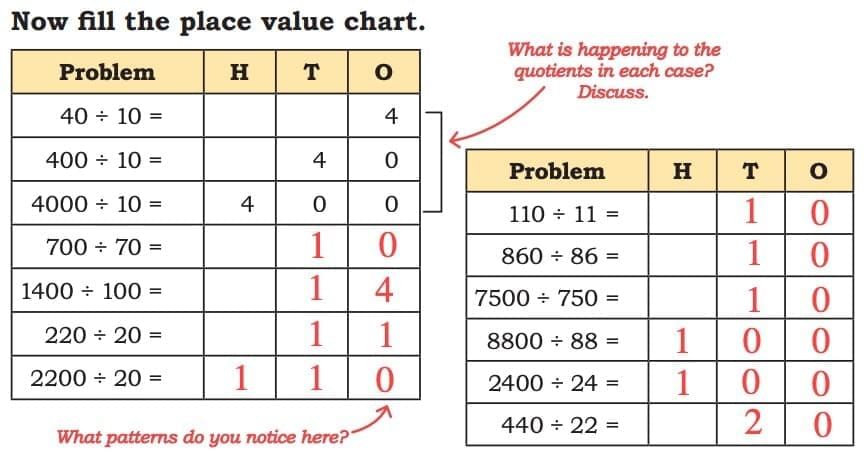
Place Value
- Dividing by 10 moves the digits 1 place to the right in the place-value chart.
- Dividing by 100 moves the digits 2 places to the right.
- Dividing by 1000 moves the digits 3 places to the right.
- In decimal numbers, the decimal point moves left the same number of places as the zeros in the divisor.
Finding Place Values:
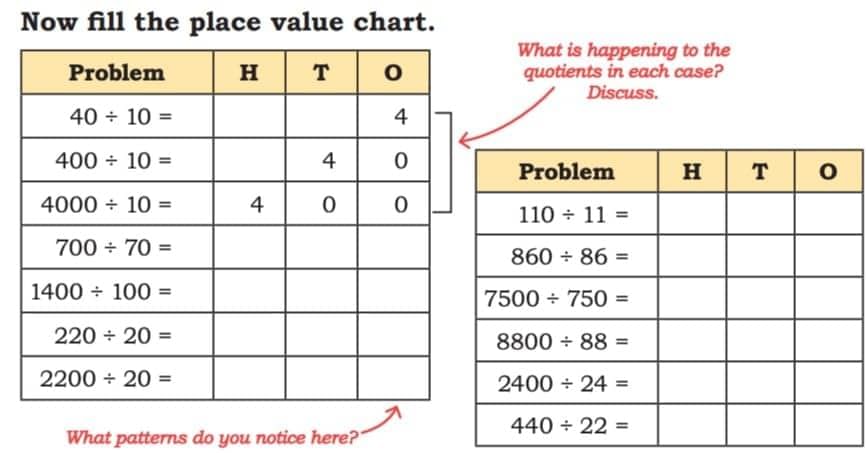
Sol:
What is happening to the quotients in each case? Discuss.
- Dividing by 10, 100, or 1000 makes the number 10, 100, or 1000 times smaller.
- This is why the digits move to the right in the place-value chart.
- If both numbers change by the same factor, the answer stays the same.
What patterns do you notice here?
- Digits move right when dividing by 10, 100, or 1000.
- More zeros in the divisor → more places moved.
- Some answers are round numbers like 10, 100, or 1000.
Application Problems
- We use division to share things equally, so everyone gets the same.
- Division helps to make equal groups when we arrange items.
- It is used to find the value for one item, one hour, or one day.
- We use division in daily life for money, time, distance, work, and other things.
- Knowing division helps us solve word problems easily.
Distance Problem:
Q: Sabina cycles 160 km in 20 days and the same distance each day. How many kilometres does she cycle each day?
Sol: Sabina cycles 160 km in 20 days.
To find how many kilometres she cycles each day:
Thus, she cycles 8 km each day.
Mental Strategies for Division
We can divide faster in our mind by using some simple tricks:- Break big numbers into smaller, easy parts, then add the results.
- Use numbers that are close and easy to divide, then adjust the answer.
- Halve the number twice if dividing by 4, and three times if dividing by 8.
- Use multiplication tables to see how many groups fit in the number.
- Estimate a close answer first to check if your result makes sense.

Try some strategies:
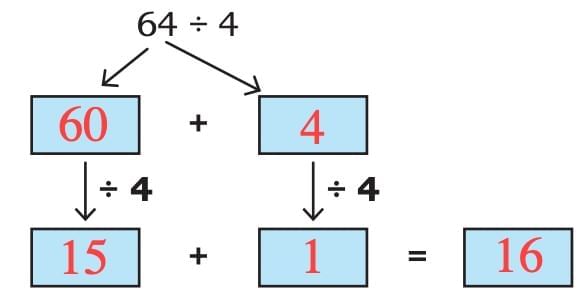
1.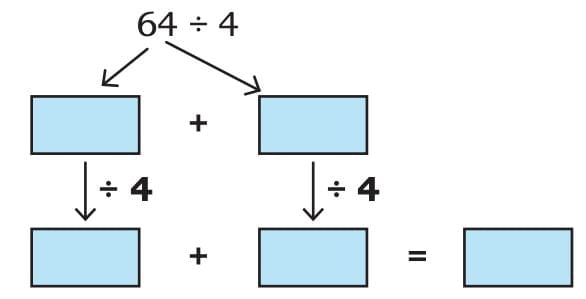
Sol:
- Break 64 into 60 + 4
Divide each part by 4:
60 ÷ 4 = 15
4 ÷ 4 = 1- Add the results: 15 + 1 = 16
So, 64 ÷ 4 = 16
2. 
Sol:
Halve 168 → 84
Halve 84 → 42
Halve 42 → 21
So, 168 ÷ 8 = 21
Susie’s Farm in Kerala
Partial-Quotients Division & Estimation
Sometimes we can solve big division problems in easy steps. This is called partial-quotients division.
- Take away big groups of the divisor again and again.
- Each time, write how many groups you took away.
- Add all the groups to get the answer.
- Bigger groups mean fewer steps.
- First, make a guess (estimate) to help choose group sizes and check your answer.
Susie and Sunitha have a large coconut farm, and they harvested 1,117 coconuts in April. They sold 582 coconuts equally to 6 regular customers. How many coconuts did each customer get?
They sold 582 ÷ 6 coconuts to each customer. Susie and Sunitha both gave two different methods: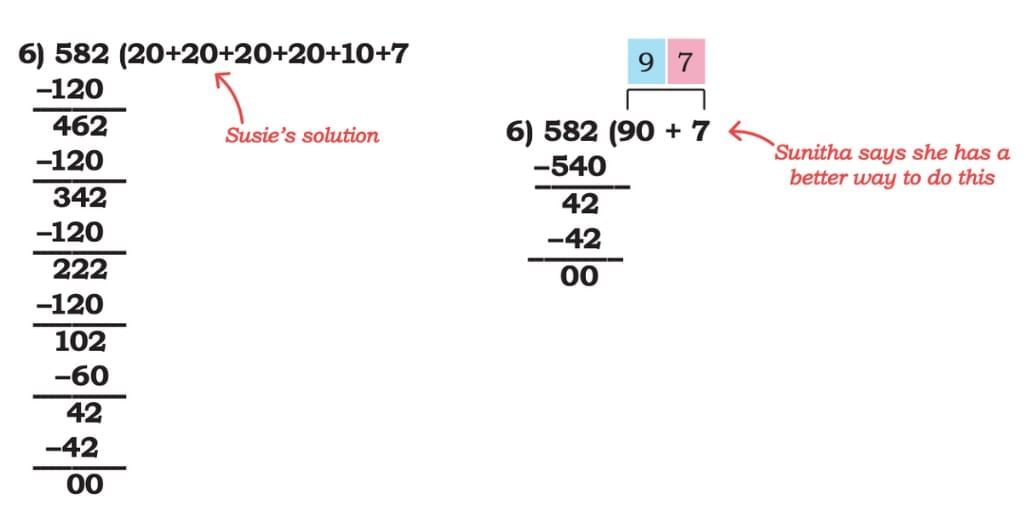 Each customer gets 97 coconuts.
Each customer gets 97 coconuts.
Do you think Sunitha’s method is better? Discuss which one you would prefer and why.
Sol: I think Sunitha’s method is better because it is faster. She takes away a big number first, so there are fewer steps. Susie’s way works, but it takes more time because she takes away small numbers many times.
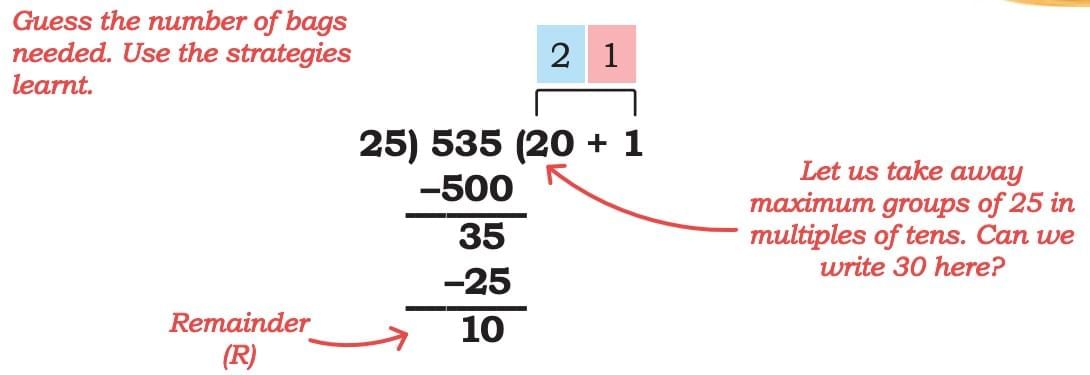
Each bag can hold 25 coconuts. How many bags would be needed to pack 97 coconuts?
Sol: 3 bags will hold 75 coconuts. They will need another bag to fill the remaining coconuts. So, each person will get 4 bags.
They pack the remaining coconuts for drying and extracting oil. They can pack 25 coconuts in each bag. How many bags will they need to pack the remaining coconuts?
Sol: The number of coconuts left after selling 582 coconuts is 1117 – 582 = 535. The number of bags needed is 535 ÷ 25.
They need 21 full bags and 1 more bag to pack the 10 remaining coconuts, that is, 22 bags.
Remainders & the Division Relationship
Sometimes, the divisor (D) does not completely divide the dividend (N) and leaves a remainder (R)
Words to know:
- Dividend = the big number we’re dividing.
- Divisor = how many in each group.
- Quotient = the number of full groups.
- Remainder = what’s left over.
The rule is: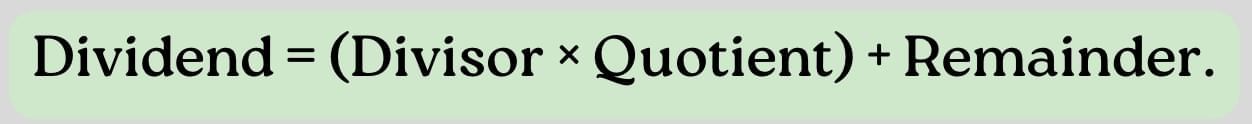 N = (D × Q) + R
N = (D × Q) + R
- The remainder is always smaller than the divisor.
- A remainder of 0 means no leftovers.
- A non-zero remainder means there are leftovers.
Identify the remainder, if any. Check if N = D × Q + R:
1. 902 ÷ 16
Sol:
Now, after solving the above, we have:
N= 902
D= 16
Q= 56
R= 6
Checking if N = D × Q + R :
902 = 16 x 56 + 6
902 = 896 + 6
902 = 902
Hence, proved that both sides are equal.
Kalpavruksha Coconut Oil
In a particular year, Susie and Sunitha used 4376 coconuts for extracting coconut oil. They can extract 1 litre of oil from 8 coconuts. What quantity of oil were they able to extract?
Sol: They would get 4376 ÷ 8 litres of coconut oil.
They extracted 547 L of oil in the year.
Division Using Place Value
- Start with the biggest place value (the leftmost digit) when dividing a number.
- Check if the divisor fits into the number or part of it.
- Regroup if the part you’re dividing is smaller than the divisor.
- Place zeros in the quotient if needed when the number doesn’t divide evenly.
- Continue dividing by moving to smaller place values (tens, hundreds, ones).
- After dividing, check the answer by multiplying the quotient with the divisor.
Candle Distribution Problem:
Sunitha’s mother has 62 candies to be distributed equally among 5 children. How many candies would each child get? She shows the following way of doing division using place value.
1. 62 ÷ 5 → Divide 62 into 5 equal parts.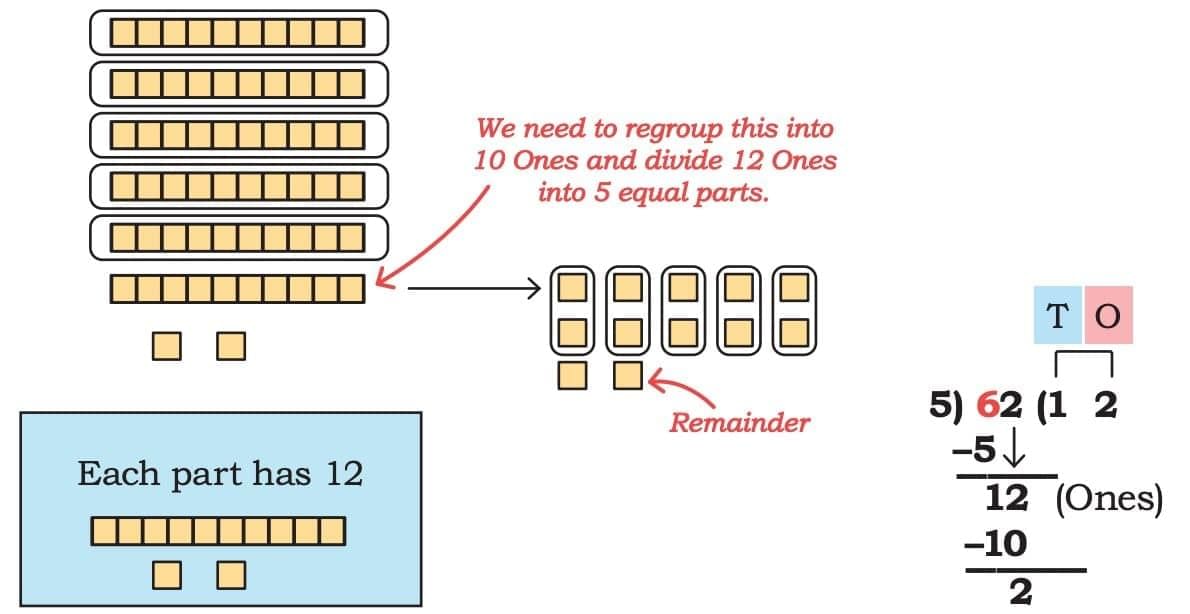
Sol:
- Sunitha’s mother has 62 candies to be shared among 5 children.
- First, divide the tens place (6 tens = 60) by 5.
Each child gets 12 candies from this (because 60 ÷ 5 = 12).- We are left with 2 candies as remainder (because 62 – 60 = 2).
- So, each child gets 12 candies and 2 candies are left over.
Answer: 62 ÷ 5 = 12 remainder 2
2. 75 ÷ 8 → Divide 75 into 8 equal parts.
Sol:
We need to divide 75 into 8 equal groups.
First, check: 8 × 9 = 72.
Subtract: 75 – 72 = 3.
So, each child gets 9 candies and 3 candies are left over.
Answer: 75 ÷ 8 = 9 remainder 3
3. 324 ÷ 3 → Divide 324 into 3 equal parts.

Sol: 324 = 3 Hundreds + 2 Tens + 4 Ones
3 Hundreds ÷ 3 = 1 Hundred.
2 Tens ÷ 3 → Not possible without regrouping, so everyone gets 0 Tens.
Regroup 2 Tens into Ones.
20 Ones + 4 Ones = 24 Ones.
24 Ones ÷ 3 = 8 Ones.
4. 136 ÷ 6 → Divide 136 into 6 equal parts.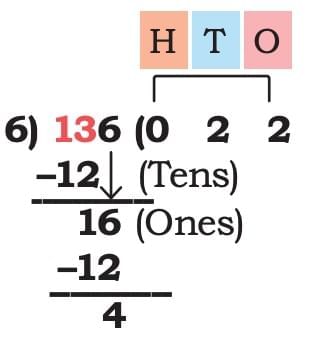
Sol: 136 = 1 Hundred + 3 Tens + 6 Ones.
1 Hundred ÷ 6 → not possible without regrouping into Tens
Regroup 1 Hundred into 10 Tens.
Total 13 Tens. Continue dividing.
Extended Word Problems
- Some problems use both multiplication and division.
- First, you might need to multiply to find a total.
- Then, divide to share that total equally or find how many groups there are.
- Do the steps in the correct order to get the right answer.
Solved Example:
Naina bought 5 kg of ice cream as a birthday treat for her 23 friends. 400 g of ice cream was left after everyone had an equal share. How much ice cream did each of her friends eat?
Sol: Naina bought 5 kg of ice cream.
That means she had 5000 grams of ice cream. (1 kg = 1000 grams)After the party, 400 grams were left.
So, the ice cream that was eaten =
grams.She had 23 friends. Everyone got the same amount.
To find each friend’s share:
grams.Thus, each friend ate 200 grams of ice cream.
Data Handling via Division
- Division helps you find missing numbers in tables or charts.
- It can also help to check totals and see if they add up correctly.
- Sometimes, you need to divide to find the value for one item or unit.
Vegetable Market:
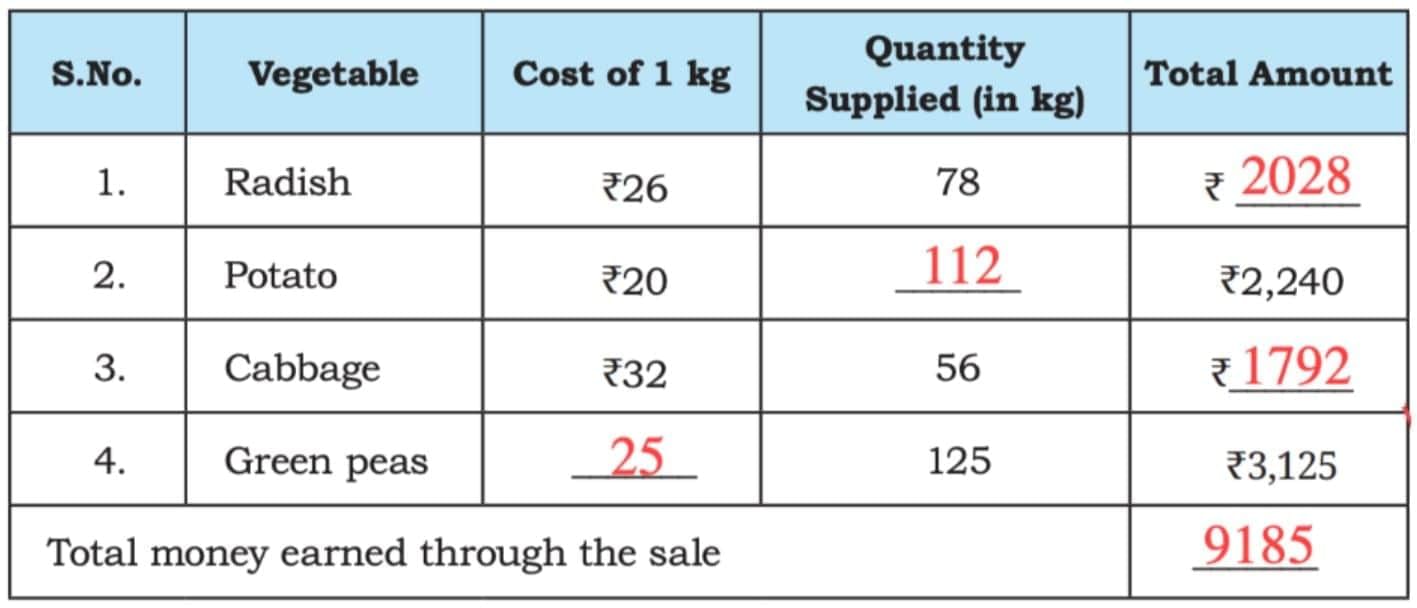
Munshi Lal has a big farm in Bihar. Every Saturday, he sells the vegetables from his farm at Sundar Sabzi Mandi. Munshi ji maintains a detailed record of the quantity of vegetables he sends to the Mandi and the cost of each vegetable.
The following table shows his record book on one Saturday. His naughty grandson has erased some numbers from his record book. Help Munshi Lal complete the table.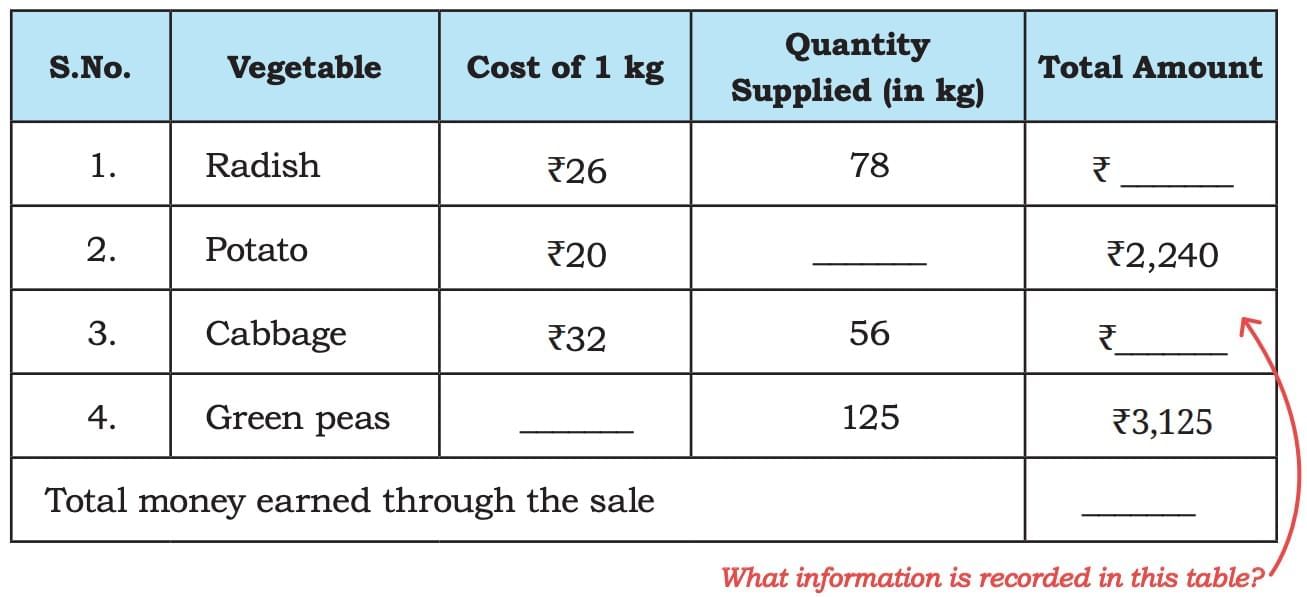
Sol:
- Radish:
Cost of 1 kg = ₹26
Quantity = 78 kg
Total amount = ₹2028- Potato:
Total amount = ₹2240
Cost of 1 kg = ₹20
Quantity = 112 kg- Cabbage:
Cost of 1 kg = ₹32
Quantity = 56 kg
Total amount = ₹1792- Green peas:
Total amount = ₹3125
Quantity = 125 kg
Cost of 1 kg = ₹25- Total money earned:
Total = ₹9185
Mathematical Statements
- When you see a math statement, decide if it’s always, sometimes, or never true.
- Think carefully about why the statement is right or wrong, and explain your reasoning.
Solved Example:
Complete the following statements such that they are true.
(a) 7 × 6 = ____ + 17
(b) 87 + 6 = ____ × 31
(c) 63 + ____ = 74 – 4
(d) ____ ÷ 9 = 16 ÷ 2
Sol:
(a)7 × 6 = ____ + 17(b)87 + 6 = ____ × 31
- 7 × 6 = 42
- 42 = ____ + 17
- 42 − 17 = 25
Answer: 7 × 6 = 25 + 17(c)63 + ____ = 74 − 4
- 87 + 6 = 93
- 93 = ____ × 31
- 93 ÷ 31 = 3
Answer: 87 + 6 = 3 × 31(d)____ ÷ 9 = 16 ÷ 2
- 74 − 4 = 70
- 63 + ____ = 70
- 70 − 63 = 7
Answer: 63 + 7 = 74 − 4
- 16 ÷ 2 = 8
- ____ ÷ 9 = 8
- 8 × 9 = 72
Answer: 72 ÷ 9 = 16 ÷ 2
The document Coconut Farm Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT is a part of the Class 5 Course Mathematics (Maths Mela) Class 5 - New NCERT.
All you need of Class 5 at this link: Class 5
|
35 videos|318 docs|7 tests
|
FAQs on Coconut Farm Chapter Notes - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What is the basic definition of multiplication and how is it used in everyday life? |  |
Ans. Multiplication is a mathematical operation that combines equal groups to find the total amount. It is often described as repeated addition. In everyday life, multiplication is used in various situations, such as calculating the total cost of multiple items, determining how many hours are in several days, or figuring out the area of a rectangle by multiplying its length by its width.
| 2. How does division relate to multiplication, and why is this connection important? |  |
Ans. Division is the inverse operation of multiplication. This means that if you multiply a number by another and then divide the result by one of those numbers, you will get the other number back. This connection is important because it helps in understanding how to solve problems involving sharing or grouping items. It allows for checking work done in multiplication and helps in developing a deeper understanding of numbers and their relationships.
| 3. What are some common patterns observed in the division process? |  |
Ans. Common patterns in division include the ability to identify factors of numbers and recognize that dividing by zero is undefined. Additionally, when dividing by 10, 100, or 1,000, the decimal point moves to the left for each zero in the divisor. In simpler cases, division by 2 results in even numbers, while division by odd numbers can help determine divisibility rules, such as those used in fractions.
| 4. How does place value impact the process of division? |  |
Ans. Place value plays a crucial role in division as it helps to understand how to break down larger numbers into manageable parts. When dividing, knowing the value of each digit in a number allows for easier calculations, especially when dealing with multi-digit dividends and divisors. By focusing on one place value at a time, such as hundreds, tens, or units, students can perform division more systematically and accurately.
| 5. What mental strategies can be employed to simplify division problems? |  |
Ans. Mental strategies for simplifying division problems include using estimation, breaking down numbers into smaller factors, and using compatible numbers that are easier to divide. For example, when dividing 48 by 6, one might round 48 to 50 and divide by 6, then adjust the answer down. Using known multiplication facts to find quotients can also speed up the process, as can recognizing patterns in division that align with multiplication tables.
Related Searches