Connecting Differentiability and Continuity: Determining When Derivatives Do and .... Chapter Notes | Calculus AB - Grade 9 PDF Download
Welcome to your guide on connecting differentiability and continuity in AP Calculus! This topic is essential for mastering derivatives by exploring when they exist and how they relate to continuity. We'll combine our understanding of continuity over intervals with derivative concepts to strengthen your skills.
Continuity and Differentiability: The Connection
In AP Calculus, most functions you'll encounter are both continuous and differentiable. However, issues arise when a function fails to meet one or both conditions. To review continuity, check out this guide:
Confirming Continuity over an Interval.
A function is differentiable if it has a derivative at every point in its domain, meaning the graph is smooth and resembles a straight line when zoomed in closely (not necessarily horizontal). For example, consider the graph of cos(x). Zooming in at the point (0, 1), the curve appears linear, indicating differentiability.
For a function to be differentiable at a specific point, the left-hand and right-hand derivatives must match the derivative at that point:
limx→a⁻ f'(x) = limx→a⁺ f'(x) = f'(a)
Key rule: If a function is differentiable, it must be continuous. However, continuity does not guarantee differentiability. A function may fail to be differentiable if it is discontinuous, has a sharp change in slope, or features a vertical tangent.
When Is a Function Not Differentiable?
Let's explore scenarios where a function lacks differentiability, using graphs to illustrate each case.
1. Discontinuous Graphs
Discontinuity often leads to non-differentiability because the derivatives from the left and right sides of a point don't align.
Example: Unequal Derivatives
For most discontinuous graphs, we can see that the derivatives approaching the point from either side will not be equal.
For example,
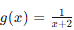 looks like the following in the graph below. Since the denominator cannot equal 0, x ≠ 2. The domain of this graph is (−∞,−2)∪(−2,∞).
looks like the following in the graph below. Since the denominator cannot equal 0, x ≠ 2. The domain of this graph is (−∞,−2)∪(−2,∞).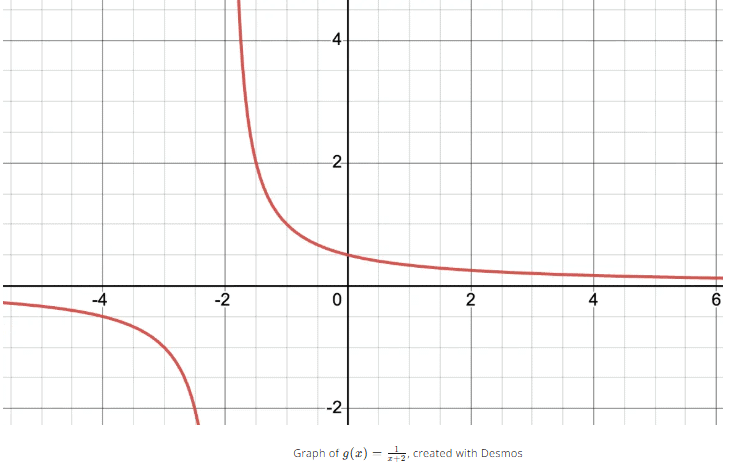
We also see that 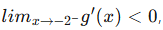 while
while 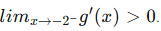 Hence, we can conclude that this graph is not continuous, and therefore not differentiable at x = −2.
Hence, we can conclude that this graph is not continuous, and therefore not differentiable at x = −2.
Jump Discontinuity
A jump discontinuity occurs when the function's values jump abruptly. For instance, in a graph where limx→2⁻ f'(x) > 0 and limx→2⁺ f'(x) < 0, the derivatives are unequal, confirming non-differentiability.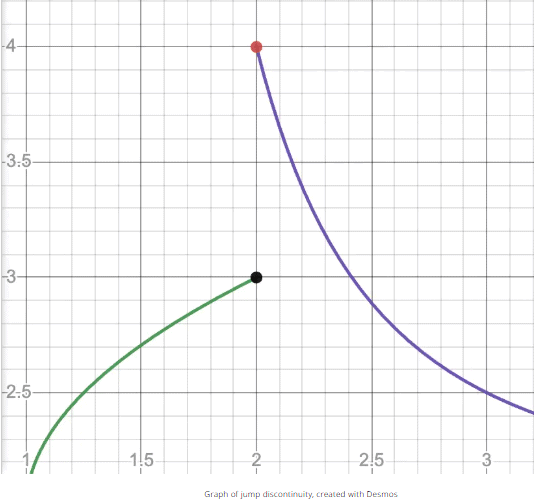
Removable Discontinuity
For a removable discontinuity, we have to take it a step further. Take a look at the graph of  below. We can see that there is a removable discontinuity at x = 2.
below. We can see that there is a removable discontinuity at x = 2.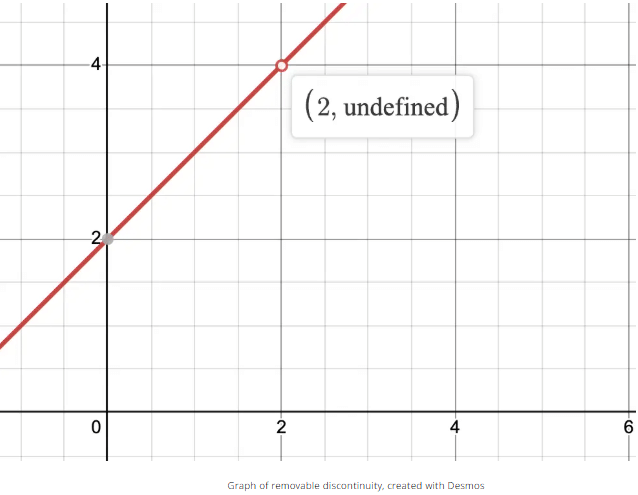 We can determine, by hand or with a calculator, that the derivative is equal to 1 at all points except for x = 2. But what about at x = 2? The calculator will tell us that the derivative is undefined, or does not exist. Since limx→2−h′(x) = limx→2+h′(x) but ≠ f′(2), we determine that the function is not differentiable at x = 2.
We can determine, by hand or with a calculator, that the derivative is equal to 1 at all points except for x = 2. But what about at x = 2? The calculator will tell us that the derivative is undefined, or does not exist. Since limx→2−h′(x) = limx→2+h′(x) but ≠ f′(2), we determine that the function is not differentiable at x = 2.
Therefore, if the curve is discontinuous at a point, it cannot be differentiable.
2. Vertical Tangents
Consider f(x) = 2(x + 2)(1/3) below.
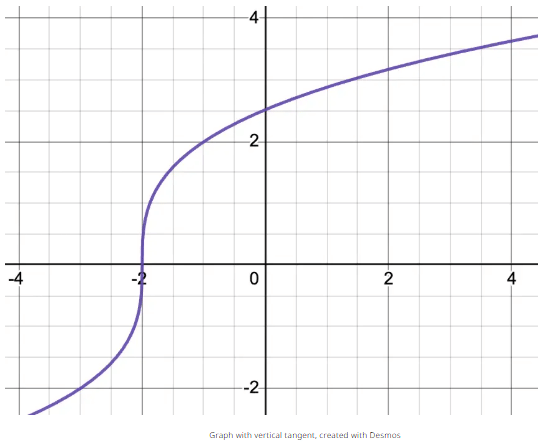
What would the derivative at x = −2 be equal to? If we think about the slope of a line tangent to f(x)$ at $x = -2, the slope would be ∞ because the change in y values would be a number divided by the change in x values: 0. Therefore, the derivative at x = −2 does not exist, and makes the curve not differentiable at x = −2.
3. Corners and Cusps
We can determine that a curve will not be differentiable at a corner or a cusp because the derivative will not approach the same value on both sides of the point. Additionally, there may be a vertical tangent! Let's observe the graphs below.
This is the graph of
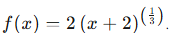 We can see that this graph would have a vertical tangent line as we approach x = 3, so it cannot be differentiable.
We can see that this graph would have a vertical tangent line as we approach x = 3, so it cannot be differentiable.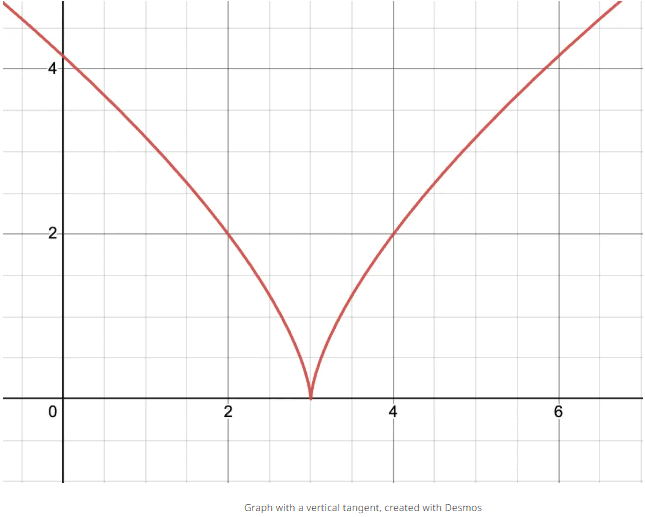 Let’s look at another graph! This is the graph of g(x) = ∣x∣. This function has a corner, and is not diffferentiable because limx→0−g′(x)<0 while limx→0−g′(x) > 0, and cannot be equal.
Let’s look at another graph! This is the graph of g(x) = ∣x∣. This function has a corner, and is not diffferentiable because limx→0−g′(x)<0 while limx→0−g′(x) > 0, and cannot be equal.
Practice Problems
Problem 1: Graphically Identifying Differentiability
Determine the number of points where the following piecewise function is not differentiable.
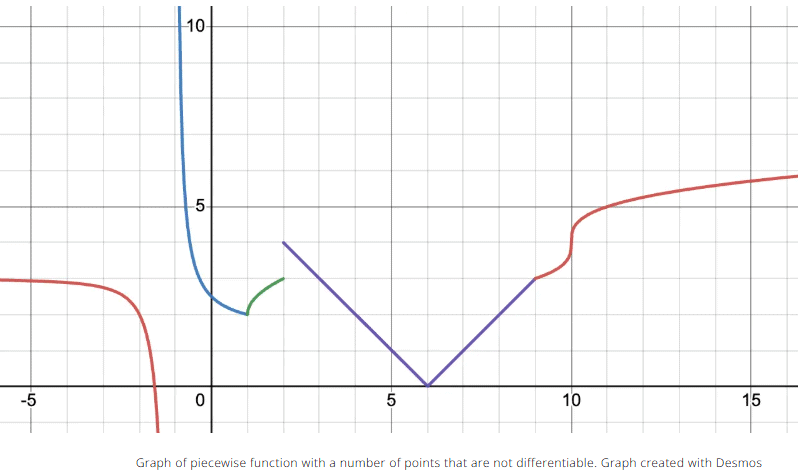
Solution: The function has 6 points of non-differentiability:
- Infinite discontinuity at x = -1.
- Jump discontinuity at x = 2.
- Cusp at (1, 2).
- Cusp at (9, 3).
- Corner at (6, 0).
- Vertical tangent at (10, 4).
Problem 2: Determining Differentiability Algebraically
From the 2003 AP Calculus AB Exam, courtesy of College Board.
Given the piecewise function:
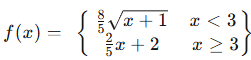
Assuming f(x) is continuous at x = 3, is it differentiable?
Solution: Step 1: Left-hand derivative (x < 3)
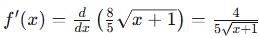
Therefore, 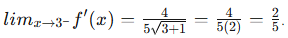
Step 2: Right-hand derivative (x ≥ 3)
For f(x) = (2/5)x + 2, the derivative is:
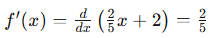
Therefore, 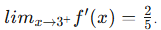
Step 3: Derivative at x = 3
To check the derivative at the point, we need to take the derivative of the equation representing the function when x = 3, which is the same as when x ≥ 3.
Therefore, 
Now we check that all of the limits equal each other, and find that the function $f(x)$ is differentiable at x = 3 ! Check the graph below to confirm our work.

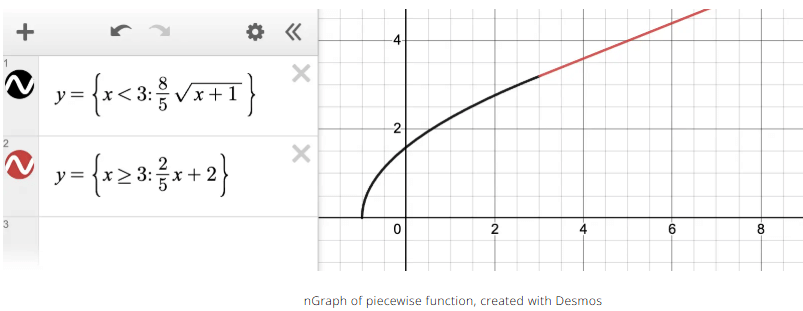 As we can see from the graph, the function f(x) is smooth at x=3, and is therefore differentiable.
As we can see from the graph, the function f(x) is smooth at x=3, and is therefore differentiable.
Closing
You're mastering these concepts, and with practice, you'll navigate derivatives and continuity with confidence. Determining when derivatives exist and ensuring continuity is a crucial skill in AP Calculus. As you encounter questions on the exam, remember to check for domain restrictions and assess piecewise continuity.
Key Terms to Know
- Continuous Function: A function with no breaks, holes, or jumps, drawable without lifting the pen.
- Differentiability: A function has a derivative at every point in its domain, indicating a smooth graph with a defined slope.
- Differentiable Function: A function with derivatives throughout its domain, allowing slope calculation at any point.
- Function: A relation where each input has exactly one output.
- Limit Definition of the Derivative: A formula to find a function’s instantaneous rate of change as the change in x approaches zero.
- Limit: The value a function approaches as the input nears a specific point or infinity.
- Piecewise Function: A function defined by different rules for different intervals of the input.
- Point of Discontinuity: A point where the function’s graph breaks or jumps, losing continuity.
- Step Function: A piecewise function that jumps between constant values, resembling a staircase.
|
26 videos|75 docs|38 tests
|
FAQs on Connecting Differentiability and Continuity: Determining When Derivatives Do and .... Chapter Notes - Calculus AB - Grade 9
| 1. What is the relationship between continuity and differentiability in functions? |  |
| 2. What are common examples of functions that are not differentiable? |  |
| 3. How can you determine if a function is not differentiable at a specific point? |  |
| 4. Can a function be differentiable on an interval and fail to be differentiable at a point within that interval? |  |
| 5. Why is understanding the connection between continuity and differentiability important in calculus? |  |















