Open App

Class 8 Exam > Class 8 Notes > Mathematics Class 8 ICSE > Chapter Notes: Constructions (Using Ruler and Compasses Only)

Constructions (Using Ruler and Compasses Only) Chapter Notes | Mathematics Class 8 ICSE PDF Download

Q: 4. How can you construct parallel lines using a ruler and compass?

Ans. To construct parallel lines, follow these steps:1. Start with a line segment AB.2. Choose a point C not on line AB, where you want the parallel line to be drawn.3. Using a compass, draw a circle centered at point A, and another at point B with the same radius.4. Mark the intersections of the circles with a line drawn through point C.5. Draw a line through point C that passes through the intersection points; this line will be parallel to line AB.

Q: 5. What are the steps to construct a rectangle using a ruler and compass?

Ans. To construct a rectangle, follow these steps:1. Draw a line segment AB, which will be one side of the rectangle.2. At point A, use a compass to draw a circle with a radius equal to the desired width of the rectangle.3. Repeat this step at point B.4. Mark the intersection points of the circles as C and D.5. Draw straight lines connecting points A to C and B to D.6. Finally, connect points C and D to complete the rectangle ABCD.

Table of contents
Introduction
Construction of an Angle
Construction of Bisector of a Line Segment
Construction of Perpendicular Bisector of a Line Segment
Construction of Perpendicular to a Line
Constructions of Parallel Lines
Construction of Quadrilateral ABCD
Construction of Parallelogram ABCD
Construction of Rectangle ABCD
Construction of Rhombus ABCD
Construction of Square ABCD

Introduction

This chapter focuses on geometric constructions using only a ruler and compasses, essential tools for creating accurate geometric figures without measuring angles or lengths directly. It covers constructing angles, bisecting lines and angles, drawing perpendiculars, parallel lines, and various quadrilaterals like parallelograms, rectangles, rhombuses, and squares. These constructions help develop precision and understanding of geometric properties, laying the foundation for more advanced geometric concepts.

Construction of an Angle

Constructing an angle equal to a given angle:
Draw a line segment of any length as the base for the new angle.
Using the vertex of the given angle as the center, draw an arc to intersect both arms of the angle, marking two points.
With the same radius, draw an arc from the vertex of the new angle to intersect the base at a point.
Measure the distance between the two points on the given angle using the compass.
Using this distance, draw an arc from the point on the new base to intersect the previous arc, marking another point.
Join the vertex of the new angle to this intersection point to form the desired angle.
Example:To construct ∠DEF equal to ∠ABC:
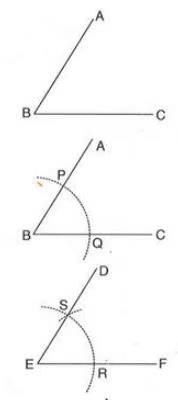
- Draw line segment EF.
- With B as center, draw an arc cutting AB at P and BC at Q.
- With E as center and same radius, draw an arc cutting EF at R.
- With R as center and radius equal to PQ, draw an arc intersecting the previous arc at S.
- Join E to S and extend to D. Thus, ∠DEF = ∠ABC.
Drawing the bisector of a given angle:
Draw an arc with the vertex of the angle as the center, intersecting both arms at two points.
From these two points, draw arcs of equal radius inside the angle to intersect at a point.
Join the vertex to this intersection point to create the bisector, dividing the angle into two equal parts.
Example:To draw the bisector of ∠ABC:
- With B as center, draw an arc cutting AB at D and BC at E.
- With D and E as centers, draw arcs of equal radius (more than half DE) intersecting at O.
- Join B to O and extend to P. Thus, BP is the bisector, and ∠ABP = ∠PBC = ½ ∠ABC.
Construction of angles of 60°, 30°, 90°, and 45°:
Angle of 60°:
- Draw a line segment of any length.
- With one endpoint as the center, draw an arc to intersect the segment at a point.
- Using this intersection point as the center with the same radius, draw another arc to intersect the first arc.
- Join the first endpoint to this intersection point to form a 60° angle.
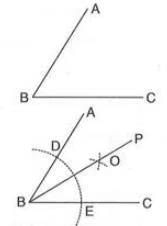
- Example:To construct ∠ABC = 60°:
  - Draw line segment BC.
  - With B as center, draw an arc cutting BC at D.
  - With D as center and same radius, draw an arc intersecting the previous arc at E.
  - Join B to E and extend to A. Thus, ∠ABC = 60°.
Angle of 30°:
- Construct a 60° angle as described above.
- Draw the bisector of this 60° angle to get a 30° angle.
- Example:To construct ∠PBC = 30°:
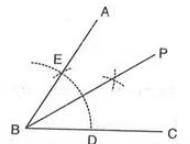
  - Construct ∠ABC = 60° as above.
  - Draw BP, the bisector of ∠ABC. Thus, ∠PBC = ½ × 60° = 30°.
Angle of 90°:
- Draw a line segment of any length.
- With one endpoint as the center, draw an arc to intersect the segment.
- With this intersection point as the center, draw another arc to intersect the first arc.
- With this new intersection point as the center, draw a third arc to intersect the first arc again.
- From the last two intersection points, draw arcs to intersect each other above the line.
- Join the original endpoint to this new intersection point to form a 90° angle.
- Example:To construct ∠ABC = 90°:
  - Draw line segment BC.
  - With B as center, draw an arc cutting BC at D.
  - With D as center and same radius, draw an arc cutting the previous arc at E.
  - With E as center and same radius, draw an arc cutting the first arc at F.
  - With E and F as centers and radius more than half EF, draw arcs intersecting at P.
  - Join B to P and extend to A. Thus, ∠ABC = 90°.
Angle of 45°:
- Construct a 90° angle as described above.
- Draw the bisector of this 90° angle to get a 45° angle.
- Example:To construct ∠ABC = 45°:
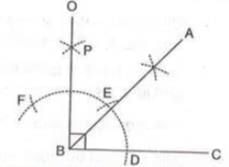
  - Draw line segment BC.
  - Construct ∠OBC = 90° as above.
  - Draw BA, the bisector of ∠OBC. Thus, ∠ABC = ½ × 90° = 45°.

Construction of Bisector of a Line Segment

First Method:
Draw the given line segment.
At one endpoint, construct an angle of any measure.
At the other endpoint, construct an equal angle.
From each angle’s arm, cut off equal lengths.
Join these two points to bisect the line segment.
Example:To bisect line segment BC:
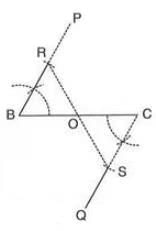
- Draw line segment BC.
- At B, construct ∠PBC of any measure.
- At C, construct ∠QCB = ∠PBC.
- From BP, cut BR of any length, and from CQ, cut CS = BR.
- Join R and S. RS intersects BC at O, where OB = OC.
Alternative Method:
Draw the line segment.
With one endpoint as the center and radius more than half the segment’s length, draw arcs on both sides.
With the other endpoint as the center and the same radius, draw arcs to intersect the previous arcs.
Join the intersection points to bisect the line segment.
Example:To bisect line segment BC:
Draw line segment BC.
With B as center and radius more than half BC, draw arcs on both sides.
With C as center and same radius, draw arcs intersecting at P and Q.
Join P and Q. PQ intersects BC at O, where OB = OC.

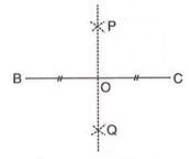
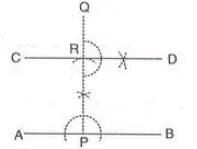
Construction of Perpendicular Bisector of a Line Segment

Draw the given line segment.
With one endpoint as the center and radius more than half the segment’s length, draw arcs on both sides.
With the other endpoint as the center and the same radius, draw arcs to intersect the previous arcs.
Join the intersection points to create a line that bisects the segment and is perpendicular to it.
Example:To construct the perpendicular bisector of BC:

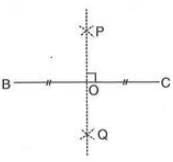
Constructions (Using Ruler and Compasses Only) Chapter Notes | Mathematics Class 8 ICSE

Draw line segment BC.
With B as center and radius more than half BC, draw arcs on both sides.
With C as center and same radius, draw arcs intersecting at P and Q.
Join P and Q. PQ intersects BC at O, where OB = OC and ∠POC = 90°.

Construction of Perpendicular to a Line

Perpendicular at a given point on the line:
With the given point as the center, draw an arc to intersect the line at two points.
From these two points, draw arcs of equal radius to intersect inside or outside the line.
Join the given point to this intersection point to form the perpendicular.
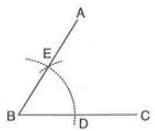
Example:To construct a perpendicular at point P on line AB:
- With P as center, draw an arc cutting AB at C and D.
- With C and D as centers, draw arcs of equal radius (more than half CD) intersecting at O.
- Join P to O. Thus, OP is perpendicular, with ∠OPA = ∠OPB = 90°.
Perpendicular from an external point to the line:
With the external point as the center, draw an arc to intersect the line at two points.
From these two points, draw arcs of equal radius to intersect on the opposite side of the line.
Join the external point to this intersection point, intersecting the line to form the perpendicular.
Example:To construct a perpendicular from point P to line AB:
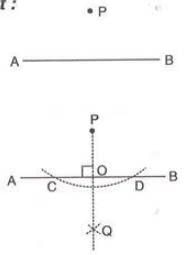
With P as center, draw an arc cutting AB at C and D.
With C and D as centers, draw arcs of equal radius (more than half CD) intersecting at Q on the other side.
Join P to Q, intersecting AB at O. Thus, OP is perpendicular, with ∠AOP = ∠BOP = 90°.

Constructions of Parallel Lines

Parallel line through a given point (First Method - Alternate Angles):
Join the given point to any point on the given line.
At the given point, construct an angle equal to the angle formed at the line’s point.
Extend this angle’s arm to form the parallel line.
Example:To construct a line parallel to AB through point P:
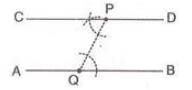
- Join P to point Q on AB.
- At P, construct ∠CPQ = ∠PQB.
- Extend CP to D. Thus, CPD is parallel to AB.
Alternative Method (Corresponding Angles):
Join the given point to a point on the line and extend it.
At the given point, construct an angle equal to the angle at the line’s point.
Extend this angle’s arm to form the parallel line.
Example:To construct a line parallel to AB through point P:
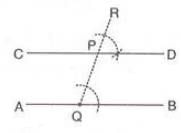
- Join QP and extend to R.
- At P, construct ∠RPD = ∠PQB.
- Extend DP to C. Thus, CPD is parallel to AB.
Parallel line at a given distance:
At any point on the given line, draw a perpendicular.
From this point, mark the given distance along the perpendicular.
At this new point, draw another perpendicular to the first perpendicular.
Extend this line to form the parallel line at the specified distance.
Example:To construct a line parallel to AB at 3.6 cm:
- At point P on AB, draw PQ perpendicular to AB.
- With P as center and radius 3.6 cm, draw an arc cutting PQ at R.
- At R, draw RD perpendicular to PQ.
- Extend DR to C. Thus, CD is parallel to AB at 3.6 cm.

Construction of Quadrilateral ABCD

When four sides and one angle are given:
Draw one side of the quadrilateral.
At one endpoint, construct the given angle and mark the second side.
From the other endpoint of the second side, draw an arc with the length of the third side.
From the first side’s other endpoint, draw an arc with the length of the fourth side to intersect the previous arc.
Join the points to form the quadrilateral.
Example:To construct quadrilateral ABCD with AB = 4 cm, BC = 3.6 cm, CD = 3.5 cm, DA = 3 cm, and ∠A = 60°:
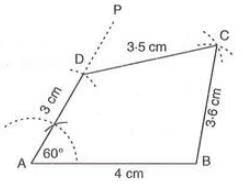
- Draw AB = 4 cm.
- At A, construct ∠PAB = 60° and cut DA = 3 cm from AP.
- With D as center and radius 3.5 cm (CD), draw an arc.
- With B as center and radius 3.6 cm (BC), draw an arc intersecting at C.
- Join CD and CB. Thus, ABCD is the quadrilateral.
When three consecutive sides and two included angles are given:

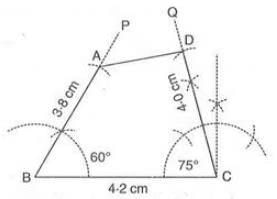
Constructions (Using Ruler and Compasses Only) Chapter Notes | Mathematics Class 8 ICSE

Draw the middle side of the three consecutive sides.
At one endpoint, construct one given angle and mark the first side.
At the other endpoint, construct the second given angle and mark the third side.
Join the endpoints to complete the quadrilateral.
When four sides and one diagonal are given:
Draw one side of the quadrilateral.
From one endpoint, draw an arc with the length of the diagonal.
From the other endpoint, draw an arc with the length of the second side to intersect the diagonal arc.
From this intersection point, draw an arc with the length of the third side.
From the first side’s other endpoint, draw an arc with the length of the fourth side to intersect the previous arc.
Join the points to form the quadrilateral.
Example:To construct quadrilateral ABCD with AB = 4 cm, BC = 3.8 cm, CD = 3.5 cm, DA = 4.2 cm, and diagonal AC = 5.5 cm:
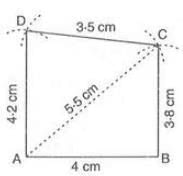
- Draw AB = 4 cm.
- With B as center and radius 3.8 cm (BC), draw an arc.
- With A as center and radius 5.5 cm (AC), draw an arc intersecting at C.
- With C as center and radius 3.5 cm (CD), draw an arc.
- With A as center and radius 4.2 cm (DA), draw an arc intersecting at D.
- Join CD and DA. Thus, ABCD is the quadrilateral.

Construction of Parallelogram ABCD

When two consecutive sides and the included angle are given:
Draw one side of the parallelogram.
At one endpoint, construct the given angle and mark the second side.
From the other endpoint of the second side, draw an arc with the length of the first side (opposite sides are equal).
From the first side’s other endpoint, draw an arc with the length of the second side to intersect the previous arc.
Join the points to form the parallelogram.
Example:To construct parallelogram ABCD with BC = 4.2 cm, CD = 3.6 cm, and ∠C = 60°:
- Draw BC = 4.2 cm.
- At C, construct ∠PCB = 60° and cut CD = 3.6 cm from CP.
- With D as center and radius 4.2 cm (AD = BC), draw an arc.
- With B as center and radius 3.6 cm (AB = CD), draw an arc intersecting at A.
- Join AB and AD. Thus, ABCD is the parallelogram.
When two consecutive sides and one diagonal are given:
Draw one side of the parallelogram.
From one endpoint, draw an arc with the length of the second side.
From the other endpoint, draw an arc with the length of the diagonal to intersect the previous arc.
From this intersection point, draw an arc with the length of the first side.
From the first side’s other endpoint, draw an arc with the length of the second side to intersect the previous arc.
Join the points to form the parallelogram.
Example:To construct parallelogram ABCD with AB = 4.5 cm, BC = 3.7 cm, and diagonal AC = 6.2 cm:
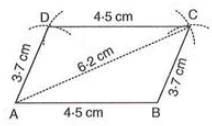
- Draw AB = 4.5 cm.
- With B as center and radius 3.7 cm (BC), draw an arc.
- With A as center and radius 6.2 cm (AC), draw an arc intersecting at C.
- With C as center and radius 4.5 cm (CD = AB), draw an arc.
- With A as center and radius 3.7 cm (AD = BC), draw an arc intersecting at D.
- Join AD and CD. Thus, ABCD is the parallelogram.
When both diagonals and the angle between them are given:
Draw one diagonal.
Construct its perpendicular bisector to find the midpoint.
Through the midpoint, draw a line at the given angle to the diagonal.
Mark half the length of the second diagonal on both sides of the midpoint along this line.
Join the endpoints to form the parallelogram.
Example:To construct parallelogram ABCD with diagonal AC = 5.5 cm, diagonal BD = 6.0 cm, and angle between them = 60°:
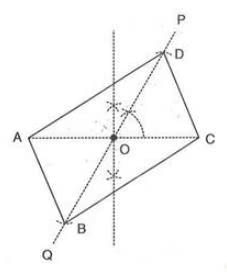
- Draw AC = 5.5 cm.
- Draw the perpendicular bisector of AC, intersecting at O (midpoint).
- Through O, construct line POQ with ∠POC = 60°.
- From PQ, cut OD = OB = 3.0 cm (½ BD).
- Join AB, BC, CD, and DA. Thus, ABCD is a parallelogram.

Construction of Rectangle ABCD

When two adjacent sides are given:
Draw one side of the rectangle.
At one endpoint, construct a 90° angle and mark the second side.
From the other endpoint of the second side, draw an arc with the length of the first side.
From the first side’s other endpoint, draw an arc with the length of the second side to intersect the previous arc.
Join the points to form the rectangle.
Example:To construct rectangle ABCD with AB = 5.0 cm and BC = 3.5 cm:
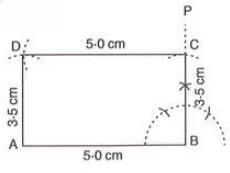
- Draw AB = 5.0 cm.
- At B, construct ∠PBA = 90° and cut BC = 3.5 cm from BP.
- With C as center and radius 5.0 cm (DC = AB), draw an arc.
- With A as center and radius 3.5 cm (AD = BC), draw an arc intersecting at D.
- Join AD and CD. Thus, ABCD is the rectangle.
When one side and one diagonal are given:
Draw the given side.
At one endpoint, construct a 90° angle.
From the other endpoint, draw an arc with the length of the diagonal to intersect the 90° angle’s arm.
From this intersection point, draw an arc with the length of the given side.
From the first side’s other endpoint, draw an arc with the length of the opposite side to intersect the previous arc.
Join the points to form the rectangle.
Example:To construct rectangle ABCD with AB = 4.8 cm and diagonal AC = 6.2 cm:
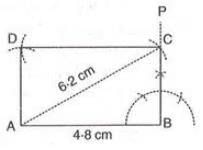
- Draw AB = 4.8 cm.
- At B, construct ∠PBA = 90°.
- With A as center and radius 6.2 cm (AC), draw an arc cutting BP at C.
- With C as center and radius 4.8 cm (CD = AB), draw an arc.
- With A as center and radius equal to BC, draw an arc intersecting at D.
- Join AD and CD. Thus, ABCD is the rectangle.
When one diagonal and the angle between the two diagonals are given:
Draw the given diagonal.
Construct its perpendicular bisector to find the midpoint.
Through the midpoint, draw a line at the given angle to the diagonal.
Mark half the length of the diagonal on both sides of the midpoint along this line.
Join the endpoints to form the rectangle.
Example:To construct rectangle ABCD with diagonal AC = 6.4 cm and angle between diagonals = 60°:
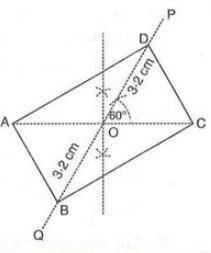
- Draw AC = 6.4 cm.
- Draw the perpendicular bisector of AC, intersecting at O (midpoint).
- Through O, construct line POQ with ∠POC = 60°.
- From OP, cut OD = 3.2 cm, and from OQ, cut OB = 3.2 cm.
- Join AB, BC, CD, and DA. Thus, ABCD is the rectangle.

Construction of Rhombus ABCD

When one side and one angle are given:
Draw one side of the rhombus.
At one endpoint, construct the given angle and mark another side.
From the other endpoint of the second side, draw an arc with the side length.
From the first side’s other endpoint, draw an arc with the side length to intersect the previous arc.
Join the points to form the rhombus.
Example:To construct rhombus ABCD with AB = 4.5 cm and ∠A = 60°:
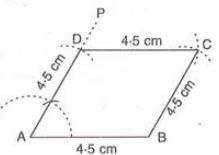
- Draw AB = 4.5 cm.
- At A, construct ∠PAB = 60° and cut AD = 4.5 cm from AP.
- With D as center and radius 4.5 cm, draw an arc.
- With B as center and radius 4.5 cm, draw an arc intersecting at C.
- Join BC and DC. Thus, ABCD is the rhombus.
When one side and one diagonal are given:
Draw one side of the rhombus.
From one endpoint, draw an arc with the length of the diagonal.
From the other endpoint, draw an arc with the side length to intersect the diagonal arc.
From this intersection point, draw an arc with the side length.
From the first side’s other endpoint, draw an arc with the side length to intersect the previous arc.
Join the points to form the rhombus.
Example:To construct rhombus ABCD with AB = 5 cm and diagonal AC = 7 cm:
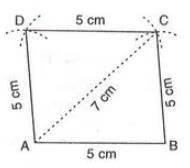
- Draw AB = 5 cm.
- With A as center and radius 7 cm (AC), draw an arc.
- With B as center and radius 5 cm, draw an arc intersecting at C.
- With C as center and radius 5 cm, draw an arc.
- With A as center and radius 5 cm, draw an arc intersecting at D.
- Join BC, CD, and DA. Thus, ABCD is the rhombus.
When both diagonals are given:
Draw one diagonal.
Construct its perpendicular bisector to find the midpoint.
Along the perpendicular bisector, mark half the length of the other diagonal on both sides of the midpoint.
Join the endpoints to form the rhombus.
Example:To construct rhombus ABCD with diagonal AC = 4.8 cm and diagonal BD = 5.4 cm:
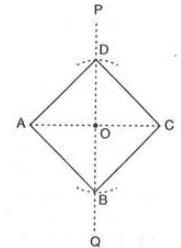
- Draw AC = 4.8 cm.
- Draw the perpendicular bisector PQ of AC, intersecting at O.
- From OP, cut OD = 2.7 cm, and from OQ, cut OB = 2.7 cm (½ BD).
- Join AB, BC, CD, and DA. Thus, ABCD is the rhombus.

Construction of Square ABCD

When one side is given:
Draw one side of the square.
At one endpoint, construct a 90° angle and mark another side.
From the other endpoint of the second side, draw an arc with the side length.
From the first side’s other endpoint, draw an arc with the side length to intersect the previous arc.
Join the points to form the square.
Example:To construct square ABCD with side AB = 4.5 cm:
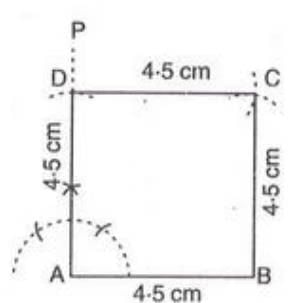
- Draw AB = 4.5 cm.
- At A, construct ∠PAB = 90° and cut AD = 4.5 cm from AP.
- With D as center and radius 4.5 cm, draw an arc.
- With B as center and radius 4.5 cm, draw an arc intersecting at C.
- Join BC and DC. Thus, ABCD is the square.
When a diagonal is given:
Draw the given diagonal.
Construct its perpendicular bisector to find the midpoint.
Along the perpendicular bisector, mark half the length of the diagonal on both sides of the midpoint.
Join the endpoints to form the square.
Example:To construct square ABCD with diagonal AC = 6.4 cm:
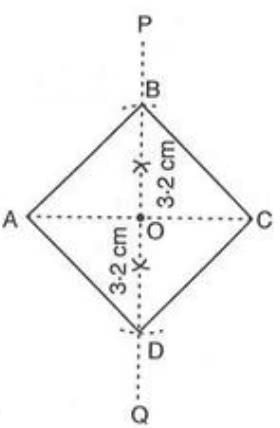
- Draw AC = 6.4 cm.
- Construct perpendicular bisector POQ of AC, intersecting at O.
- From OP, cut OB = 3.2 cm, and from OQ, cut OD = 3.2 cm (½ AC).
- Join AB, BC, CD, and DA. Thus, ABCD is the square.

The document Constructions (Using Ruler and Compasses Only) Chapter Notes | Mathematics Class 8 ICSE is a part of the Class 8 Course Mathematics Class 8 ICSE.

All you need of Class 8 at this link: Class 8

	Mathematics Class 8 ICSE 23 videos\|98 docs\|14 tests

Mathematics Class 8 ICSE

23 videos|98 docs|14 tests

Join Course for Free

FAQs on Constructions (Using Ruler and Compasses Only) Chapter Notes - Mathematics Class 8 ICSE

1. What tools are needed for constructions using ruler and compasses?

Ans. To perform constructions using a ruler and compasses, you need a straightedge (ruler without markings) and a compass. These tools allow you to draw straight lines and circles, which are essential for various geometric constructions.

2. How do you construct the bisector of a line segment?

Ans. To construct the bisector of a line segment, follow these steps: 1. Draw the line segment AB. 2. Place the compass at point A and draw a circle with radius greater than half of AB. 3. Without changing the compass width, place the compass at point B and draw another circle. 4. Mark the points where the two circles intersect as C and D. 5. Draw a straight line through points C and D; this line is the bisector of segment AB.

3. What is the method to construct a perpendicular bisector of a line segment?

Ans. To construct a perpendicular bisector of a line segment, follow these steps: 1. Draw the line segment AB. 2. Using a compass, place it at point A and draw a circle that exceeds the length of half of segment AB. 3. Keeping the same compass width, place it at point B and draw another circle. 4. Mark the intersection points of the two circles as C and D. 5. Draw a straight line through points C and D; this line is the perpendicular bisector of segment AB.

4. How can you construct parallel lines using a ruler and compass?

Ans. To construct parallel lines, follow these steps: 1. Start with a line segment AB. 2. Choose a point C not on line AB, where you want the parallel line to be drawn. 3. Using a compass, draw a circle centered at point A, and another at point B with the same radius. 4. Mark the intersections of the circles with a line drawn through point C. 5. Draw a line through point C that passes through the intersection points; this line will be parallel to line AB.

5. What are the steps to construct a rectangle using a ruler and compass?

Ans. To construct a rectangle, follow these steps: 1. Draw a line segment AB, which will be one side of the rectangle. 2. At point A, use a compass to draw a circle with a radius equal to the desired width of the rectangle. 3. Repeat this step at point B. 4. Mark the intersection points of the circles as C and D. 5. Draw straight lines connecting points A to C and B to D. 6. Finally, connect points C and D to complete the rectangle ABCD.

About this Document

4.86/5 Rating

Oct 06, 2025 Last updated

Related Exams

Class 8

Document Description: Chapter Notes: Constructions (Using Ruler and Compasses Only) for Class 8 2025 is part of Mathematics Class 8 ICSE preparation. The notes and questions for Chapter Notes: Constructions (Using Ruler and Compasses Only) have been prepared according to the Class 8 exam syllabus. Information about Chapter Notes: Constructions (Using Ruler and Compasses Only) covers topics like Introduction, Construction of an Angle, Construction of Bisector of a Line Segment, Construction of Perpendicular Bisector of a Line Segment, Construction of Perpendicular to a Line, Constructions of Parallel Lines, Construction of Quadrilateral ABCD, Construction of Parallelogram ABCD, Construction of Rectangle ABCD, Construction of Rhombus ABCD, Construction of Square ABCD and Chapter Notes: Constructions (Using Ruler and Compasses Only) Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Constructions (Using Ruler and Compasses Only).

Introduction of Chapter Notes: Constructions (Using Ruler and Compasses Only) in English is available as part of our Mathematics Class 8 ICSE for Class 8 & Chapter Notes: Constructions (Using Ruler and Compasses Only) in Hindi for Mathematics Class 8 ICSE course. Download more important topics related with notes, lectures and mock test series for Class 8 Exam by signing up for free. Class 8: Constructions (Using Ruler and Compasses Only) Chapter Notes | Mathematics Class 8 ICSE

Description

Full syllabus notes, lecture & questions for Constructions (Using Ruler and Compasses Only) Chapter Notes | Mathematics Class 8 ICSE - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 8 ICSE | Best notes, free PDF download

Information about Chapter Notes: Constructions (Using Ruler and Compasses Only)

In this doc you can find the meaning of Chapter Notes: Constructions (Using Ruler and Compasses Only) defined & explained in the simplest way possible. Besides explaining types of Chapter Notes: Constructions (Using Ruler and Compasses Only) theory, EduRev gives you an ample number of questions to practice Chapter Notes: Constructions (Using Ruler and Compasses Only) tests, examples and also practice Class 8 tests

	Mathematics Class 8 ICSE 23 videos\|98 docs\|14 tests

Mathematics Class 8 ICSE

23 videos|98 docs|14 tests

Join Course for Free

Download as PDF

Explore Courses for Class 8 exam

mock tests for examination

Objective type Questions

video lectures

pdf

practice quizzes

Extra Questions

ppt

study material

MCQs

Constructions (Using Ruler and Compasses Only) Chapter Notes | Mathematics Class 8 ICSE

Important questions

Constructions (Using Ruler and Compasses Only) Chapter Notes | Mathematics Class 8 ICSE

Previous Year Questions with Solutions

Sample Paper

Exam

past year papers

shortcuts and tricks

Free

Constructions (Using Ruler and Compasses Only) Chapter Notes | Mathematics Class 8 ICSE

Viva Questions

Summary

Semester Notes

;

Additional Information about Chapter Notes: Constructions (Using Ruler and Compasses Only) for Class 8 Preparation

Chapter Notes: Constructions (Using Ruler and Compasses Only) Free PDF Download

The Chapter Notes: Constructions (Using Ruler and Compasses Only) is an invaluable resource that delves deep into the core of the Class 8 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Constructions (Using Ruler and Compasses Only) now and kickstart your journey towards success in the Class 8 exam.

Importance of Chapter Notes: Constructions (Using Ruler and Compasses Only)

The importance of Chapter Notes: Constructions (Using Ruler and Compasses Only) cannot be overstated, especially for Class 8 aspirants. This document holds the key to success in the Class 8 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Chapter Notes: Constructions (Using Ruler and Compasses Only)

Chapter Notes: Constructions (Using Ruler and Compasses Only) Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Chapter Notes: Constructions (Using Ruler and Compasses Only). It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Constructions (Using Ruler and Compasses Only) Notes on EduRev are your ultimate resource for success.

Chapter Notes: Constructions (Using Ruler and Compasses Only) Class 8 Questions

The "Chapter Notes: Constructions (Using Ruler and Compasses Only) Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Chapter Notes: Constructions (Using Ruler and Compasses Only) on the App

Students of Class 8 can study Chapter Notes: Constructions (Using Ruler and Compasses Only) alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Chapter Notes: Constructions (Using Ruler and Compasses Only), students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Chapter Notes: Constructions (Using Ruler and Compasses Only) is prepared as per the latest Class 8 syllabus.

Education Revolution

Signup to see your scores go up within 7 days!

Access 1000+ FREE Docs, Videos and Tests

Continue with Google

Takes less than 10 seconds to signup