Constructions Chapter Notes | Mathematics Class 6 ICSE PDF Download
Introduction
Imagine a time when there were no computers or fancy gadgets to create perfect shapes and angles. People relied on their hands, a ruler, and a compass to draw everything from straight lines to precise angles. This chapter, "Constructions," takes us back to those days, teaching us how to use simple tools to create accurate geometric figures. It's like becoming an artist and a mathematician at the same time, crafting line segments, angles, and perpendiculars with precision. Let's dive into the world of geometric constructions and learn how to build shapes step by step using just a ruler and a compass!
Construction of a Line Segment of Given Length
This method helps us draw a line segment of a specific length using a ruler and a compass.
Steps:
- Draw a line and mark a point A on it.

- Place the compass point on the zero mark of the ruler and adjust the pencil end to the desired length (e.g., 3.5 cm).
- Keep the compass opening fixed, place the point at A, and draw an arc to intersect the line at B.
- AB is the line segment of the required length.
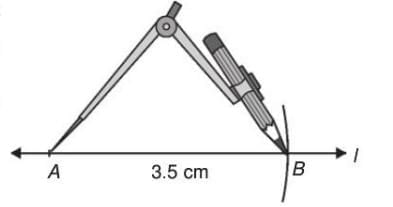
This method can also copy the length of an existing line segment.
To Draw a Perpendicular Bisector of a Line Segment
A perpendicular bisector is a line that divides a line segment into two equal parts at a 90° angle.
Steps:
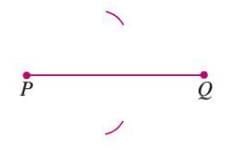
- Draw a line segment PQ.

- With P as the center, draw arcs on both sides of PQ with a radius more than half of PQ’s length.
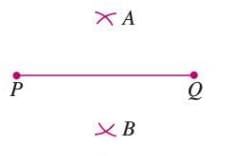
- Without changing the compass, draw arcs from Q to intersect the previous arcs at A and B.
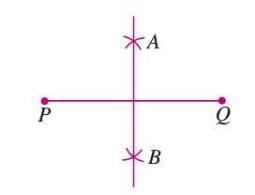
- Join A and B to form the perpendicular bisector AB.
Use of Protractor to Construct an Angle
A protractor helps draw angles of specific measures accurately.
Steps:
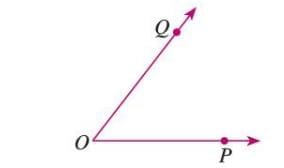
- Draw a ray OP with O as the initial point.
- Place the protractor’s midpoint at O, aligning the baseline with OP.
- Since the 0° mark aligns with OP, use the inner scale and mark the desired angle (e.g., 50°) at point Q.
- Remove the protractor and join O to Q to form ∠POQ.
Example: To construct a 50° angle:
- Draw ray OP.

- Align the protractor’s midpoint with O and baseline with OP.
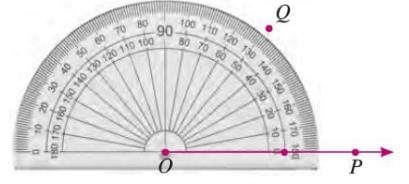
- Mark 50° on the inner scale at Q.
- Join OQ to form ∠POQ = 50°.
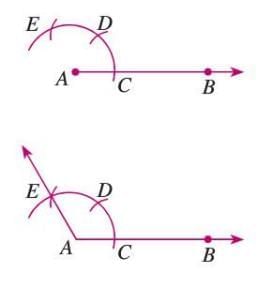
To Construct an Angle Equal to a Given Angle
This method copies an angle using a compass and ruler.
Steps:
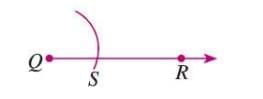
- Draw a ray QR with Q as the initial point.
- In the given angle ∠ABC, draw an arc with center B, intersecting BC at D and BA at E.
- With the same compass setting, draw an arc from Q to intersect QR at S.
- Measure the distance DE with the compass, then from S, draw an arc to intersect the previous arc at P.
- Join QP to form ∠PQR, equal to ∠ABC.
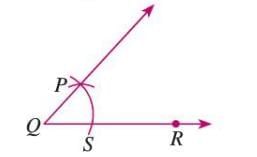
Example: To construct an angle equal to ∠ABC: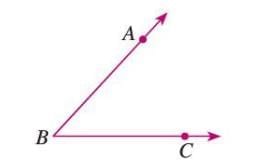
- Draw ray QR.

- From B in ∠ABC, draw an arc to intersect BC at D and BA at E.
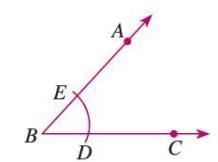
- Draw the same arc from Q to intersect QR at S.
- Set the compass to DE, draw an arc from S to intersect at P.

- Join QP to form ∠PQR = ∠ABC.
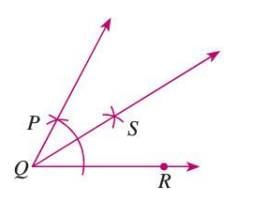
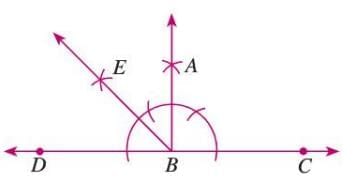
To Construct a Bisector of an Angle
An angle bisector divides an angle into two equal parts.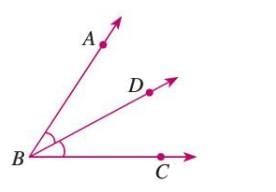
Steps:
- Draw an arc with center Q in ∠PQR, intersecting QP at S and QR at T.
- From T, draw an arc with radius more than half TS.
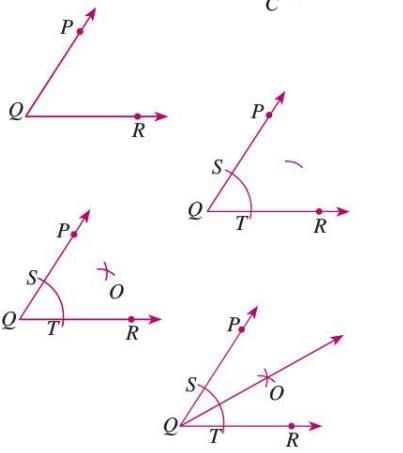
- From S, draw an arc with the same radius to intersect at O.
- Join QO to form the bisector, where ∠PQO = ∠RQO.
To Construct Angle of Standard Magnitude
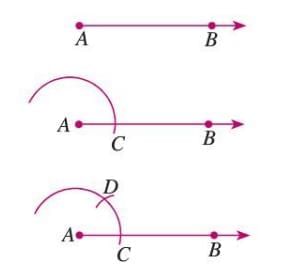
An Angle of 60°
Steps:
- Draw ray AB with A as the initial point.
- Draw an arc from A to intersect AB at C.
- With the same radius, from C, draw an arc to intersect the previous arc at D.
- Join AD to form ∠DAB = 60°.
Example: To construct a 60° angle:
- Draw ray AB.
- From A, draw an arc to intersect AB at C.
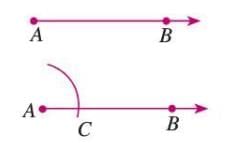
- From C, draw an arc to intersect at D.
- Join AD to form ∠DAB = 60°.
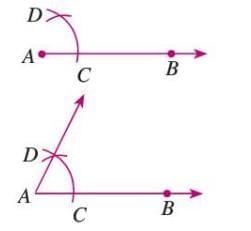
An Angle of 30°
Steps:
- Construct a 60° angle ∠PQR.
- Bisect ∠PQR by drawing ray QS, where ∠PQS = ∠RQS = 30°.
Formula: ∠PQS = ∠RQS = 60° ÷ 2 = 30°.
An Angle of 90°
Steps (Method 1):
- Draw ray AB with A as the initial point.
- Draw an arc from A to intersect AB at C.
- From C, draw an arc of radius AC to intersect at D.
- From D, draw an arc of radius AC to intersect at E.
- From D, draw an arc with radius > half DE.
- From E, draw an arc to intersect at O.
- Join AO to form ∠OAB = 90°.
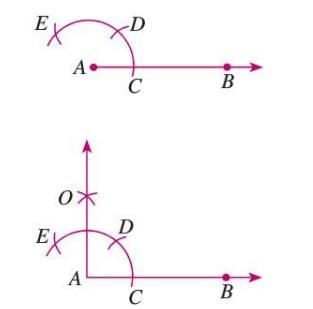
Alternate Method:
- Draw line AB with point O.
- Draw an arc from O to intersect AB at C and D.
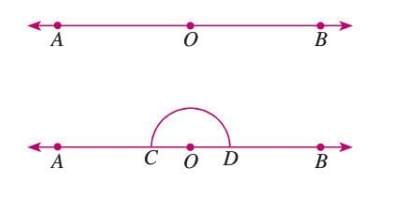
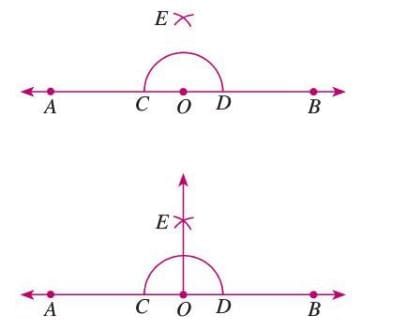
- From C, draw an arc with radius > half CD.
- From D, draw an arc to intersect at E.
- Join OE to form ∠EOB = 90°.
An Angle of 45°
Steps:
- Construct a 90° angle ∠PQR.
- Bisect ∠PQR by drawing ray QS, where ∠PQS = ∠RQS = 45°.
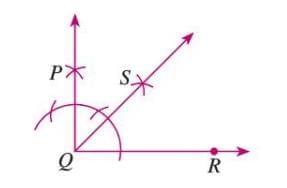
Formula: ∠PQS = ∠RQS = 90° ÷ 2 = 45°.
An Angle of 120°
Steps:
- Draw ray AB.
- Draw an arc from A to intersect AB at C.
- From C, draw an arc with the same radius to intersect at D.
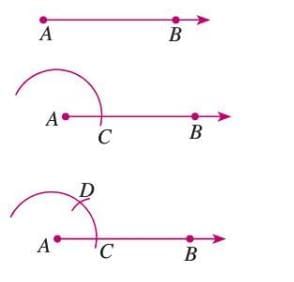
- From D, draw an arc to intersect the arc from A at E.
- Join AE to form ∠EAB = 120°.
An Angle of 135°
Steps:
- Construct a 90° angle ∠ABC.
- Bisect ∠ABD to draw ray BE, where ∠ABE = ∠DBE = 45°.
- ∠EBC = 45° + 90° = 135°.
Formula: ∠EBC = 45° + 90° = 135°.
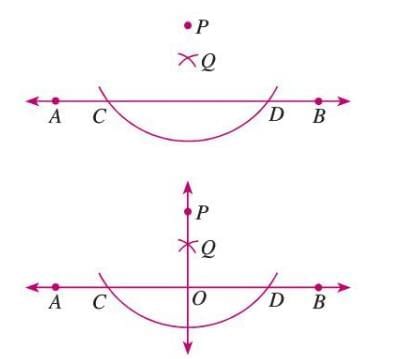
To Draw a Perpendicular to a Line
From a Point Not on the Line
Steps:
- Draw line AB and a point P not on it.
- From P, draw an arc to intersect AB at C and D.
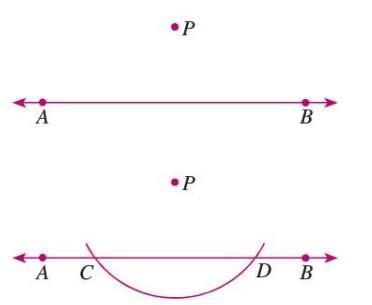
- From C, draw an arc with radius > half CD.
- From D, draw an arc to intersect at Q.
- Join PQ, intersecting AB at O, where PO is perpendicular to AB.
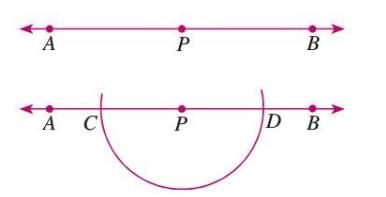
From a Point on the Line
Steps:
- Draw a line AB with point P on it.
- From P, draw an arc to intersect AB at C and D.
- From C, draw an arc with radius more than half CD.
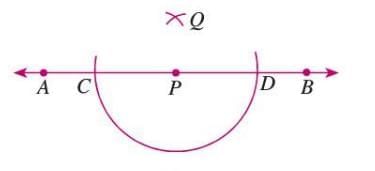
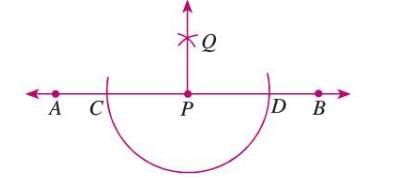
- From D, draw an arc to intersect at Q.
- Join PQ, which is perpendicular to AB.
|
44 videos|202 docs|24 tests
|
FAQs on Constructions Chapter Notes - Mathematics Class 6 ICSE
| 1. What are the steps to construct a line segment of a given length? |  |
| 2. How can I draw a perpendicular bisector of a line segment? |  |
| 3. What is the procedure to use a protractor to construct an angle? |  |
| 4. How do you construct an angle equal to a given angle? |  |
| 5. What is the method to construct a bisector of an angle? |  |
















