Decimals Chapter Notes | Mathematics Olympiad for Class 3 PDF Download
| Table of contents |

|
| Introduction |

|
| What is a Decimal? |

|
| How to Read a Decimal? |

|
| Types of Decimals |

|
Introduction
A decimal is a numerical representation comprising both an integer and a fractional component. Positioned between integers, decimal numbers express the value of quantities as a combination of a whole number and a fraction thereof.

For example, in the given image, we have one whole pizza and a half of another pizza. This can be represented in two ways:
Fractional form: In fraction form, we can write that there is one and one-half of a pizza. That is  pizza.
pizza.
Decimal form: When expressing it in decimal form, we represent this as 1.5 pizzas. In this notation, the dot serves as the decimal point. The digit preceding the dot, namely "1," signifies a complete pizza, while the digit following the decimal point signifies the additional half pizza or the fractional portion.
You might have seen decimal numbers like these when you go grocery shopping or on a weighing machine.

What is a Decimal?

Decimals result from dividing a whole into smaller units. A decimal number comprises two elements: a whole number segment and a fractional segment. The place value system for the whole part of a decimal mirrors that of whole numbers. The fractional part of the decimal is obtained by progressing to the right of the decimal point. The accompanying illustration depicts the decimal place value chart.
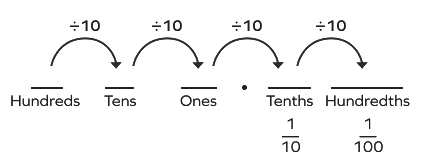
Note that as we go from left to right in the decimal place value system, each values is 1/100 times smaller than the value to its left.
- The first place after the decimal point is called the “tenths”, which represents a place value of 1/1000 of the whole or one-tenth of the whole. In decimal form, this fraction is written as “0.1”. Such fractions whose denominator is 10 or a positive power of 10 is called a decimal fraction.
- The second place is called the “hundredths”, which represents a place value of 1/100 of the whole or one-hundredth of the whole. In numerical form, this decimal fraction is written as “0.01”.
- And the third place is called the “thousandths”, which represents a place value of 1/1000 of the whole or one-thousandth of the whole. In numerical form, this decimal fraction is written as “0.001”.
Here’s an example of a decimal number 17.48, in which 17 is the whole number, while 48 is the decimal part.

How to Read a Decimal?
- Informally, one can read a decimal by pronouncing the whole part as if it were a regular whole number, and then interpreting the decimal point as "point," followed by individually pronouncing each digit of the fractional part.
- For instance, the decimal 27.48 can be informally read as "twenty-seven point four eight."
- On the other hand, a more formal approach involves reading the whole part as a complete number, interpreting the decimal point as "and," and then pronouncing the fractional part as a whole, considering the place value of the last digit.
- For example, consider the number 34.678. In this case, the whole part is 34, and the place value of the last digit, 8, is thousandths. Therefore, the formal reading of this number would be "Thirty-four and six hundred seventy-eight thousandths."
Types of Decimals
Based on the count of digits following the decimal point, decimal numbers can be classified into two types:
- Similar decimals: Decimal numbers are considered "like" if they share the same number of digits after the decimal point. For instance, 6.34 and 2.67 both exhibit two digits after the decimal point, making them similar decimals.
- Dissimilar decimals: Decimal numbers are labeled "unlike" if they possess a varying number of digits after the decimal point. For instance, 5.3 and 6.873 differ in the number of digits after the decimal point, categorizing them as dissimilar decimals.
|
42 videos|35 docs|56 tests
|
FAQs on Decimals Chapter Notes - Mathematics Olympiad for Class 3
| 1. What is a decimal and how is it different from a whole number? |  |
| 2. How do you read a decimal number? |  |
| 3. How do you compare two decimal numbers? |  |
| 4. How can decimals be used in real life? |  |
| 5. What are some activities to help understand decimals better? |  |

|
Explore Courses for Class 3 exam
|

|

















