Differentiating Inverse Functions Chapter Notes | Calculus AB - Grade 9 PDF Download
Welcome to our AP Calculus study session! Today, we’re diving into differentiating inverse functions, building on our knowledge of the chain rule and implicit differentiation. Let’s strengthen those derivative skills!
Understanding Inverse Function Derivatives
For a differentiable and invertible function f(x), its inverse f⁻¹(x) has a derivative given by:
d/dx [f⁻¹(x)] = 1 / f'(f⁻¹(x))
If we denote the inverse of f(x) as g(x), the formula becomes:
d/dx [g(x)] = 1 / f'(g(x))
A handy way to remember this is: the derivative of the inverse is the reciprocal of the original function’s derivative. This follows because if f(a) = b, then f⁻¹(b) = a. For additional review, check out this Inverse Functions Guide.
The graph below illustrates this concept, showing that the slopes of a function and its inverse are reciprocals at corresponding points, such as f(1) = 8.
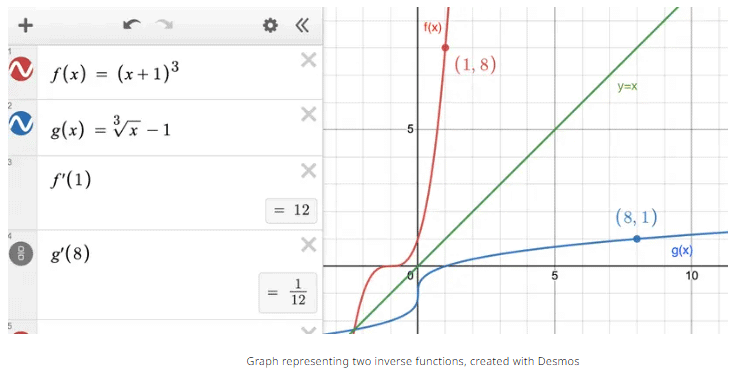
Practice Problems
Let’s solidify our understanding with a couple of practice problems.
Problem 1: Finding the Derivative of an Inverse Function
Given f(x) = 2x + 1, compute (f⁻¹)'(1).
To find (f⁻¹)'(1), which is d/dx [f⁻¹(1)], we first need f⁻¹(1). Start by determining the inverse function.
Swap variables in f(x) = 2x + 1 to get x = 2f⁻¹(x) + 1. Solve for f⁻¹(x):
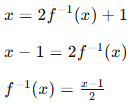
Now that we have the inverse function, we can solve for f−1(1) by plugging 1 into it.
f⁻¹(1) = (1 - 1) / 2 = 0
Next, apply the inverse derivative formula:
d/dx [f⁻¹(1)] = 1 / f'(f⁻¹(1)) = 1 / f'(0)
Since f(x) = 2x + 1, its derivative is f'(x) = 2, so f'(0) = 2. Thus:
d/dx [f⁻¹(1)] = 1 / 2
Problem 2: Tangent Line to an Inverse Function (2007 AP Calculus AB FRQ)
Consider differentiable functions f and g, where g is strictly increasing. A table provides values and derivatives at selected x values (see table from 2007 AP Calculus AB exam).

If g⁻¹ is the inverse of g, find the equation of the tangent line to y = g⁻¹(x) at x = 2.
Step a: Find the slope at x = 2
We need the slope of the tangent to y = g⁻¹(x) at x = 2. Since g(1) = 2, it follows that g⁻¹(2) = 1. Using the inverse derivative formula:
d/dx [g⁻¹(2)] = 1 / g'(g⁻¹(2)) = 1 / g'(1)
From the table, g'(1) = 5, so:
d/dx [g⁻¹(2)] = 1 / 5
Step b: Write the tangent line equation
To write the equation of the line tangent to the graph of y = g−1(x) at x = 2, we will need to plug into this formula:
y − y1 = m(x − x1).
We just calculated the value of mm, which equals 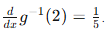 . We know that x1 = 2, and found that y(2) = g−1(2) = 1
. We know that x1 = 2, and found that y(2) = g−1(2) = 1
We can just plug it into the equation now! We can now answer that y − 1 = 1/5(x−2)
Amazing job! Our answers would have earned 3/3 points for this question. This one was tough since we had three different functions to look at: g(x), g−1(x), and g′(x), and had to take the calculations a step further.
|
26 videos|75 docs|38 tests
|
FAQs on Differentiating Inverse Functions Chapter Notes - Calculus AB - Grade 9
| 1. What is the definition of an inverse function? |  |
| 2. How do you find the derivative of an inverse function? |  |
| 3. Can all functions have inverses? |  |
| 4. What is the relationship between the derivatives of a function and its inverse? |  |
| 5. How do you apply the derivative of an inverse function in practice problems? |  |




















