Energy Chapter Notes | Technical Science for Grade 10 PDF Download
| Table of contents |

|
| Gravitational Potential Energy |

|
| Kinetic Energy |

|
| Mechanical Energy |

|
| Points to Remember |

|
| Difficult Words |

|
| Summary |

|
Gravitational Potential Energy
This section introduces gravitational potential energy, its dependence on mass and height, and how to calculate it.
What is Gravitational Potential Energy?
Definition: Gravitational potential energy is the energy an object has due to its position in a gravitational field.Explanation: When an object is lifted higher, energy is transferred to it, increasing its gravitational potential energy. This energy can later be used to do work.
Key Terms:
- Gravitational: The energy results from Earth’s gravitational pull on the object.
- Potential: The energy is stored and can be converted to other forms, like kinetic energy, to perform tasks.
Example: A heavy pole-driver head gains gravitational potential energy when lifted. When dropped, this energy drives the pole into the ground.
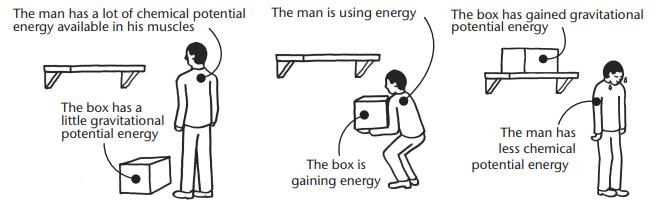
Factors Affecting Gravitational Potential Energy
- Mass: The greater the mass of an object, the more gravitational potential energy it has.
- Height: The higher an object is raised, the more gravitational potential energy it gains.
- Explanation: These factors determine how much energy is stored in an object due to its position.
Zero Height Position
Definition: The zero height position is the reference point where the height is considered zero for calculating gravitational potential energy.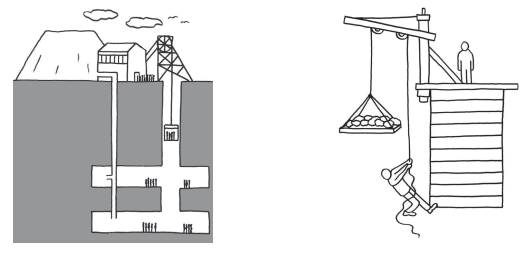 Explanation: A reference point is chosen to measure height consistently. Common choices include:
Explanation: A reference point is chosen to measure height consistently. Common choices include:
- The ground surface (e.g., for objects lifted outdoors).
- A tabletop (e.g., in classroom experiments).
Examples:
- For a mine headgear lifting materials, the ground is typically the zero height position.
- For a crane on a tower, the base of the structure might be chosen.
Calculating Gravitational Potential Energy
Formula: Gravitational potential energy = mass × acceleration due to gravity × height- In symbols: Ep = m g h (or U = m g h)
- Ep or U: Gravitational potential energy (Joules, J)
- m: Mass (kilograms, kg)
- g: Acceleration due to gravity (9.8 m/s² on Earth)
- h: Height above the reference position (meters, m)
Unit: The Joule (J) is the standard unit for energy in the SI system.
Examples:
- An object of 4 kg held 2 m above the ground:
Ep = 4 × 9.8 × 2 = 78.4 J - A 0.5 kg object at shoulder height (1.5 m) on the third floor (3 floors × 3.3 m):
Total height = (3 × 3.3) + 1.5 = 11.4 m
Ep = 0.5 × 9.8 × 11.4 = 55.9 J
Kinetic Energy
This section explores kinetic energy, the energy of motion, its forms, and how to calculate it.

What is Kinetic Energy?
Definition: Kinetic energy is the energy an object has due to its motion.Explanation: Any moving object possesses kinetic energy, which depends on its mass and speed. This energy can be transferred to other objects or used to do work.
Examples:
- In snooker, the kinetic energy of the white ball breaks up the triangle of balls, transferring energy to them.
- A skateboarder’s kinetic energy determines how high they go up a ramp. Faster speed means more kinetic energy and a higher jump.
Forms of Kinetic Energy
- Translational Motion: Energy from moving from one position to another.
Example: A soccer ball kicked across a field has translational kinetic energy. - Vibrational Motion: Energy from the vibration of atoms in a solid.
Example: Atoms in a metal bar vibrate, contributing to its kinetic energy. - Rotational Motion: Energy from spinning or rotating objects.
Example: The blades of a wind generator rotate, possessing rotational kinetic energy.

Factors Affecting Kinetic Energy
- Mass: The greater the mass of a moving object, the more kinetic energy it has.
- Speed: The faster an object moves, the more kinetic energy it has. The effect of speed is significant because kinetic energy depends on the square of the speed.
- Explanation: A heavier or faster object has more energy to transfer or do work.
Calculating Kinetic Energy
Formula: Kinetic energy = (1/2) × mass × speed squared- In symbols: Ek = (1/2) m v²
- Ek: Kinetic energy (Joules, J)
- m: Mass (kilograms, kg)
- v: Speed (meters per second, m/s)
Unit: Like gravitational potential energy, kinetic energy is measured in Joules (J).
Examples:
- A 12 kg object moving at 3 m/s:
Ek = (1/2) × 12 × 3² = 54 J - A 1.5 kg object with 14.3 J of kinetic energy:
v = sqrt((2 × 14.3) / 1.5) = 1.54 m/s - An object moving at 23 cm/s (0.23 m/s) with 0.5 J of kinetic energy:
m = (2 × 0.5) / 0.23² = 18.9 kg
Mechanical Energy
This section combines gravitational potential energy and kinetic energy into the concept of mechanical energy and introduces the conservation of energy.
What is Mechanical Energy?
Definition: Mechanical energy is the sum of an object’s gravitational potential energy and kinetic energy.Explanation: It represents the total energy of an object due to its motion (kinetic) and position (potential). Mechanical energy is conserved in ideal conditions (no air resistance or friction).
Formula: Mechanical energy = gravitational potential energy + kinetic energy
- In symbols: EM = Ep + Ek
- EM: Mechanical energy (Joules, J)
- Ep: Gravitational potential energy (Joules, J)
- Ek: Kinetic energy (Joules, J)
Examples:
- An object with Ep = 20 J and Ek = 30 J:
EM = 20 + 30 = 50 J - An object with EM = 10.5 J and Ep = 3.2 J:
Ek = 10.5 - 3.2 = 7.3 J
Calculating Mechanical Energy Components
Finding Kinetic Energy: Ek = EM - Ep
Finding Potential Energy: Ep = EM - Ek
Finding Speed or Height:
- Use Ep = m g h to find height or potential energy.
- Use Ek = (1/2) m v² to find speed or kinetic energy.
Examples:
An object with EM = 100 J, mass = 1 kg, height = 5 m:
- Ep = 1 × 9.8 × 5 = 49 J
- Ek = 100 - 49 = 51 J
- v = 10.1 m/s
A 0.7 kg object with EM = 1.1 J and Ek = 0.6 J:
- v = 1.31 m/s
- Ep = 1.1 - 0.6 = 0.5 J
- h = 0.5 / (0.7 × 9.8) = 0.07 m
Conservation of Energy (Extension)
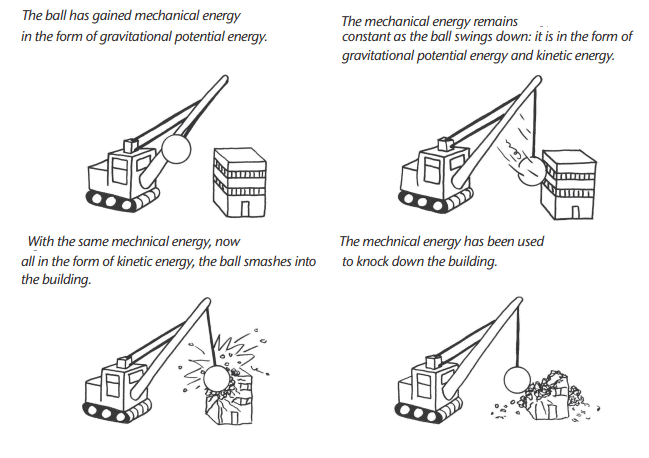
Principle: Energy cannot be created or destroyed; it can only change from one form to another.Explanation: In ideal conditions (no air resistance or friction), an object’s mechanical energy remains constant as it moves. Gravitational potential energy converts to kinetic energy, or vice versa, but the total mechanical energy stays the same.
Example: A skateboarder on a ramp:
- At the top (point A), they have maximum gravitational potential energy and zero kinetic energy.
- At the bottom (point B), potential energy is zero, and kinetic energy is maximum.
- At an intermediate point (point C), both forms of energy are present, but EM remains constant.
Mechanical Energy and Work (Extension)
Definition: Mechanical energy is the ability to do work.Explanation: Mechanical energy (potential or kinetic) can be used to perform tasks, such as knocking down a building or generating electricity.
Examples:
- A demolition crane’s steel ball gains gravitational potential energy when lifted. As it swings down, potential energy converts to kinetic energy, which does the work of demolishing a building.
- In a hydroelectric power station, the mechanical energy of moving water (kinetic energy) turns turbines to generate electricity.
Points to Remember
- Gravitational potential energy is the energy an object has due to its position in a gravitational field, calculated as Ep = m g h.
- The zero height position is the reference point where height is zero, often the ground or a tabletop.
- Kinetic energy is the energy of motion, calculated as Ek = (1/2) m v², and depends on mass and the square of speed.
- Forms of kinetic energy include translational (motion from one place to another), vibrational (atomic vibrations), and rotational (spinning objects).
- Mechanical energy is the sum of gravitational potential energy and kinetic energy, EM = Ep + Ek.
- In ideal conditions, mechanical energy is conserved, meaning the total energy remains constant as potential and kinetic energy convert between each other.
- The Joule (J) is the unit for all types of energy in the SI system.
- Mechanical energy can do work, such as demolishing buildings or generating electricity.
- Greater mass or height increases gravitational potential energy; greater mass or speed increases kinetic energy.
- The conservation of energy states that energy cannot be created or destroyed, only transformed.
Difficult Words
- Energy: The ability to do work or cause change, measured in Joules (J).
- Gravitational Potential Energy: Energy stored in an object due to its height in a gravitational field.
- Zero Height Position: The reference point where height is considered zero for energy calculations.
- Kinetic Energy: Energy an object has because it is moving.
- Translational Motion: Movement of an object from one place to another.
- Vibrational Motion: Small, rapid movements of atoms or particles, like in a solid.
- Rotational Motion: Spinning or turning motion, like a wheel or turbine.
- Mechanical Energy: The total energy of an object, combining its gravitational potential energy and kinetic energy.
- Conservation of Energy: The principle that energy cannot be created or destroyed, only changed from one form to another.
- Joule (J): The standard unit for measuring energy in the SI system.
Summary
This chapter explores energy, focusing on gravitational potential energy, kinetic energy, and mechanical energy. Gravitational potential energy, gained when an object is lifted, depends on its mass and height (Ep = m g h) and requires a zero height reference point, like the ground. Kinetic energy, the energy of motion, depends on an object’s mass and the square of its speed (Ek = (1/2) m v²) and exists in forms like translational, vibrational, and rotational motion. Mechanical energy is the sum of gravitational potential and kinetic energy (EM = Ep + Ek) and remains constant in ideal conditions due to the conservation of energy, where energy transforms between forms without loss. Mechanical energy enables work, such as demolishing structures or generating electricity. All energy is measured in Joules (J), and understanding these concepts is crucial for analyzing motion and energy transformations in real-world applications.
|
1 videos|77 docs|5 tests
|
FAQs on Energy Chapter Notes - Technical Science for Grade 10
| 1. What is gravitational potential energy and how is it calculated? |  |
| 2. How does kinetic energy differ from gravitational potential energy? |  |
| 3. What is mechanical energy and how is it related to kinetic and potential energy? |  |
| 4. Can you give examples of situations where gravitational potential energy and kinetic energy are transformed into each other? |  |
| 5. Why is it important to understand the concepts of gravitational potential energy, kinetic energy, and mechanical energy in real-life applications? |  |



















