Equal Groups Class 4 Notes Maths Chapter 9 Free PDF

Introduction

• Leo, the Lion loved visiting the watering hole, not just for a drink, but to watch his friends play! One sunny afternoon, Freddy the Frog, Squeaky the Squirrel, and Rosie the Rabbit decided to have a jumping race towards a big, juicy mango that had fallen from a tree.
• Freddy decided he would take big jumps, covering 3 steps each time. Squeaky, being smaller, took jumps of 4 steps. Rosie, with her long legs, decided on jumps of 6 steps.
• "Who will reach the mango first?" wondered Leo. "And what spots will they land on along the way?"

Just like Leo watching his friends, this chapter will help us explore how things move or are grouped in equal steps. We will learn about multiples, multiplication, and division by looking at animal jumps, arranging flowers, and even solving some magical number puzzles! Let's jump in!

Understanding Equal Groups and Multiples

When we talk about "equal groups," we mean sets that have the same number of items. Think about pairs of shoes (groups of 2), or eggs in a carton (maybe groups of 6 or 12). Understanding equal groups helps us count things faster using multiplication and share things fairly using division.

Multiplication is like making several equal jumps. 

Division is like figuring out how many equal jumps were made or how many are in each jump.

Animal Jumps

Let's go back to Leo's friends and see where they land! This helps us understand multiples.

Frog Jumps (3 Steps)

• Freddy the Frog jumps 3 steps at a time.
• Frog jumping on a number line showing multiples of 3.

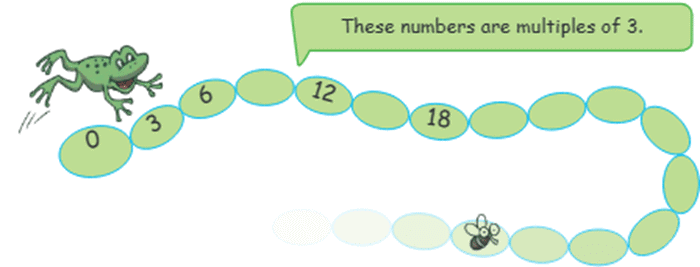
Numbers touched: 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...

These numbers are called multiples of 3.

Will the frog touch 67?

 No, because 67 is not a multiple of 3 (67 divided by 3 leaves a remainder).

Squirrel Jumps (4 Steps)

• Squeaky the Squirrel jumps 4 steps at a time.
• Squirrel jumping on a number line showing multiples of 4.

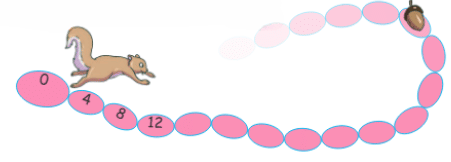
Numbers touched: 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ... 60.

These numbers are multiples of 4.

How many jumps to reach 60? 

Since 60 divided by 4 is 15, the squirrel needs to jump 15 times.

Rabbit Jumps (6 Steps)

• Rosie the Rabbit jumps 6 steps at a time.
• Rabbit jumping on a number line showing multiples of 6.

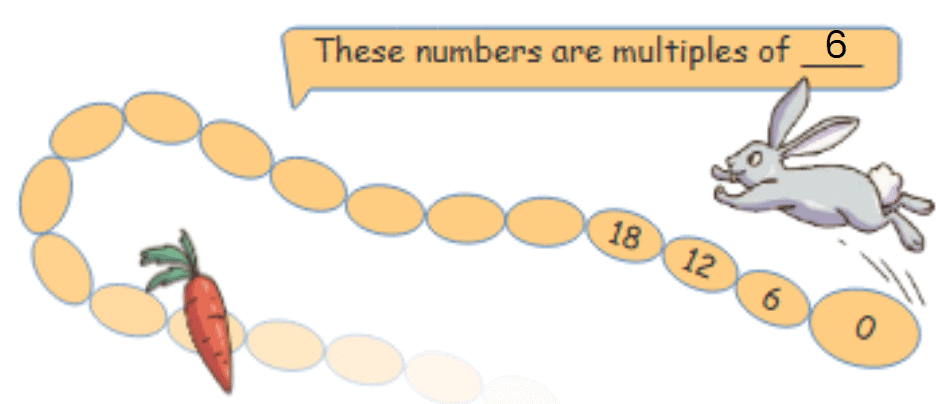
Numbers touched: 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...

These numbers are multiples of 6.

Smallest 3-digit number the rabbit will land on? 

We need the smallest multiple of 6 that is 100 or greater. 6 x 16 = 96. 6 x 17 = 102. So, the smallest 3-digit number is 102.

How many jumps to reach 102?

 The rabbit jumped 17 times.

Kangaroo Jumps (8 Steps)

• Kevin the Kangaroo joins in, jumping 8 steps at a time.
• Kangaroo jumping on a number line showing multiples of 8.

Numbers touched: 0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...

These numbers are multiples of 8.

What are Multiples?

A multiple of a number is the result you get when you multiply that number by any whole number (like 1, 2, 3, 4, ...).

Multiples of 3 are: 3 (3x1), 6 (3x2), 9 (3x3), 12 (3x4), ...

Multiples of 4 are: 4 (4x1), 8 (4x2), 12 (4x3), 16 (4x4), ...

Common Multiples

Sometimes, different animals land on the same spot! These numbers are called common multiples.

Frog (3) and Squirrel (4): Which numbers do they both touch?

 Looking at their lists, they both land on 12, 24, 36, ... These are common multiples of 3 and 4.

Rabbit (6) and Kangaroo (8): Which numbers do they both touch? 

They both land on 24, 48, 72, ... These are common multiples of 6 and 8.

Gulabo's Garden

1. Gulabo has a garden full of lily flowers. She tells us that:

• Each lily flower has 3 petals.

• She has 12 lily flowers.Gulabo's Garden

We want to find:

How many petals in 12 lily flowers?

Sol: Each flower = 3 petals
So, if we have 12 flowers, we do:

12 × 3 = ?

OR

We can break it into two parts:

• 10 flowers × 3 petals = 30 petals

• 2 flowers × 3 petals = 6 petals

Now, add them: 30 petals + 6 petals = 36 petals

Gulabo has 36 petals in 12 lily flowers!

2. Now Gulabo counts her hibiscus flowers. She knows:

• Each hibiscus flower has 5 petals.

• She counted 80 petals in total.

We want to find:

How many flowers does she have?

Sol: This is a division problem: 80 ÷ 5 = ?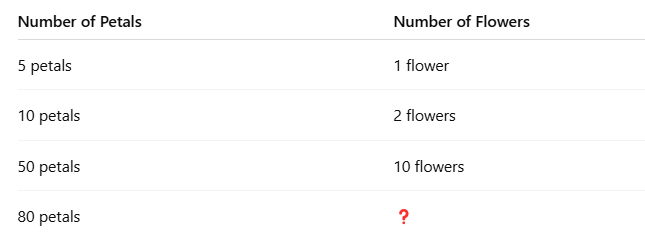

Now think:
How many groups of 5 fit into 80?

We can divide:

Gulabo has 16 hibiscus flowers.

The Doubling Magic

Doubling means multiplying by 2.

Magician Anvi doubling flowers. Anvi starts with 23 flowers. 

Abracadabra! She doubles them.

Now she has 23 x 2 = 46 flowers.

Note: When you double any whole number, the result is always an even number. The ones digit of a doubled number can only be 0, 2, 4, 6, or 8. You can never get 1, 3, 5, 7, or 9 in the ones place after doubling a whole number.

Multiplication Chart Patterns

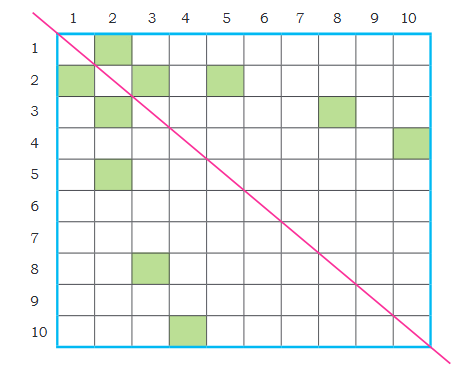10x10 Multiplication Chart

Filling a multiplication chart reveals many patterns!

Symmetry: Row 7 (7, 14, 21...) is the same as Column 7 (7, 14, 21...). This is because multiplication is commutative (a x b = b x a).

Even Rows: Rows 2, 4, 6, 8, 10 contain only even numbers because you are multiplying by an even number.

Odd Rows: Rows 1, 3, 5, 7, 9 contain a mix of odd and even numbers (Odd x Odd = Odd, Odd x Even = Even).

Ones Digit Patterns: Look at the last digit in each row. 

For example, in row 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80. The ones digits are 8, 6, 4, 2, 0, 8, 6, 4, 2, 0... a repeating pattern!

Multiples of Tens

Let's understand how multiples of tens work using some examples!

1. Counting Wheels in Tricycles

• A tricycle has 3 wheels.

• If we want to count the wheels in 10 tricycles, we can do this by multiplying:

  $10\times 3=30wheels in 10 tricycles.10\; \backslash times\; 3\; =\; 30\; \backslash quad\; \backslash text\{wheels\; in\; 10\; tricycles.\}$ wheels in 10 tricycles.

• If we want to count the wheels in 20 tricycles, we multiply:

  $20\times 3=60wheels in 20 tricycles.20\; \backslash times\; 3\; =\; 60\; \backslash quad\; \backslash text\{wheels\; in\; 20\; tricycles.\}$wheels in 20 tricycles.

  We can also break it down like this:

  $10\times 3=\mathrm{30\; and }and10\times 3=30so\mathrm{ so\; 30}+30=60.10\; \backslash times\; 3\; =\; 30\; \backslash quad\; \backslash text\{and\}\; \backslash quad\; 10\; \backslash times\; 3\; =\; 30\; \backslash quad\; \backslash text\{so\}\; \backslash quad\; 30\; +\; 30\; =\; 60.$

2. Counting Wheels in Cars

Now, let's think about cars. Each car has 4 wheels.

• If we want to count the wheels in 10 cars, we multiply:

  $10\times 4=40wheels in 10 cars.10\; \backslash times\; 4\; =\; 40\; \backslash quad\; \backslash text\{wheels\; in\; 10\; cars.\}$ wheels in 10 cars.

• If we want to count the wheels in 30 cars, we can do:

  $30\times 4=120wheels in 30 cars.30\; \backslash times\; 4\; =\; 120\; \backslash quad\; \backslash text\{wheels\; in\; 30\; cars.\}$wheels in 30 cars.

  This can also be broken into smaller steps:

  $10\times 4=40,10\times 4=40,10\times 4=4010\; \backslash times\; 4\; =\; 40,\; \backslash quad\; 10\; \backslash times\; 4\; =\; 40,\; \backslash quad\; 10\; \backslash times\; 4\; =\; 40$

  Then:

  $40+40+40=120$

What Happens When the Number of Groups is a Multiple of 10?

When we have a multiple of 10 (like 10, 20, 30, etc.) in the problem, it simply means that we are counting in big groups. It is easier to multiply by 10 or its multiples because the pattern is simple, and the answer increases by 10, 20, 30, etc. each time!

$40\; +\; 40\; +\; 40\; =\; 120$

Multiplying using 10s 

Think of 18 as 10 + 8.

10 boxes have 4 cupcakes in each. So, 10 x 4 = 40.

8 boxes have 4 cupcakes in each. So, 8 x 4 = 32.

⇒ (10 x 4) + (8 x 4)

⇒ 40 + 32 = 72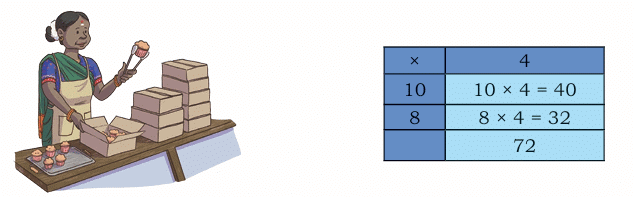

Division

1. A factory has ordered 58 wheels for the small tempos that they make. Each tempo has 3 wheels. In how many tempos can they fix the wheels?

Sol: We will divide 58 ÷ 3 — because we are sharing 58 wheels into groups of 3.

We will start by subtracting groups of 3 wheels (each group makes one tempo) until we use up most of the wheels.

Step 1:

We know:

• 10 tempos need $10\times 3=30$ wheels.

So,

• After making 10 tempos, 30 wheels are used.

• Wheels left:

  $58-30=28wheels\; left.58\; -\; 30\; =\; 28\; \backslash text\{\; wheels\; left.\}$ wheels left.

Step 2:

We know:

• 5 tempos need $5\times 3=155\; \times \; 3\; =\; 15$ wheels.

So,

• After making 5 more tempos, 15 wheels are used.

• Wheels left:

  $28-15=13wheels\; left.28\; -\; 15\; =\; 13\; \backslash text\{\; wheels\; left.\}$ wheels left.

Step 3:

We know:

• 3 tempos need $3\times 3=93\; \times \; 3\; =\; 9$ wheels.

So,

• After making 3 more tempos, 9 wheels are used.

• Wheels left:

  $13-9=4wheels\; left.13\; -\; 9\; =\; 4\; \backslash text\{\; wheels\; left.\}$ wheels left.

We know:

• 1 tempo needs $1\times 3=3$ wheels.

So,

• After making 1 more tempo, 3 wheels are used.

• Wheels left:

  $4-3=1wheel\; left.4\; -\; 3\; =\; 1\; \backslash text\{\; wheel\; left.\}$4−3 =1 wheel left.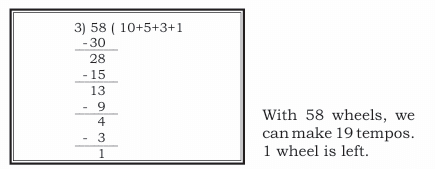

No! Because 1 wheel is not enough to make a tempo (we need 3 wheels per tempo).

2.  A dairy farm has many cows. Chippi the lizard is surprised to see 88 legs. How many cows are there in the farm?

Sol: Each cow has 4 legs. So we divide:

$88÷4=$Number of cows

Let’s take away groups of 10 cows at a time:

Each group of 10 cows has:

$10\times 4=40legs10\; \times \; 4\; =\; 40\; \backslash text\{\; legs\}$  legs

Now subtract from the total:

$88-40=48legs\; left88\; -\; 40\; =\; 48\; \backslash text\{\; legs\; left\}$ legs left

Take out another group of 10 cows:

$10\times 4=40legs10\; \times \; 4\; =\; 40\; \backslash text\{\; legs\}$ legs

$48-40=8legs\; left48\; -\; 40\; =\; 8\; \backslash text\{\; legs\; left\}$ legs left

Now use 2 more cows (2 × 4 = 8 legs)

$8-8=0legs\; left8\; -\; 8\; =\; 0\; \backslash text\{\; legs\; left\}$ legs left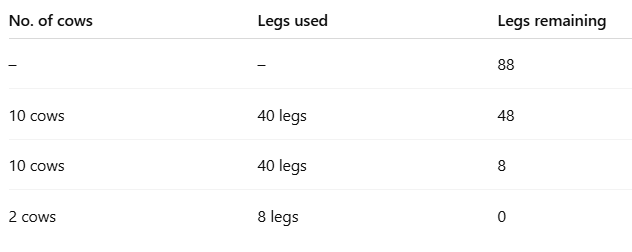

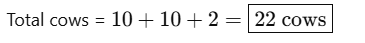
Multiples of 100

When you multiply by hundreds, you are doing a small multiplication first, and then adding two zeros.

Example 1: 2 people on each bike

• If there are 100 bikes and each bike has 2 people:

  • 100 × 2 = 200 people

• If there are 200 bikes:

  • 200 × 2 = 400 people

How did we find it?
First, multiply 2 × 2 = 4 and then add two zeros → 400

When multiplying numbers like 100, 200, 500:

• First multiply the number without zeros (like 1, 2, or 5) with the given number.

• Then add the two zeros from 100.

More Multiplication

1. Big electric autorickshaws run in small towns of India and can carry 8 passengers. How many people can travel in 125 such autos in a single round?

Sol: Let’s break 125 autos into parts we can easily multiply:

• 100 autos

• 20 autos

• 5 autos

We will multiply each by 8 passengers.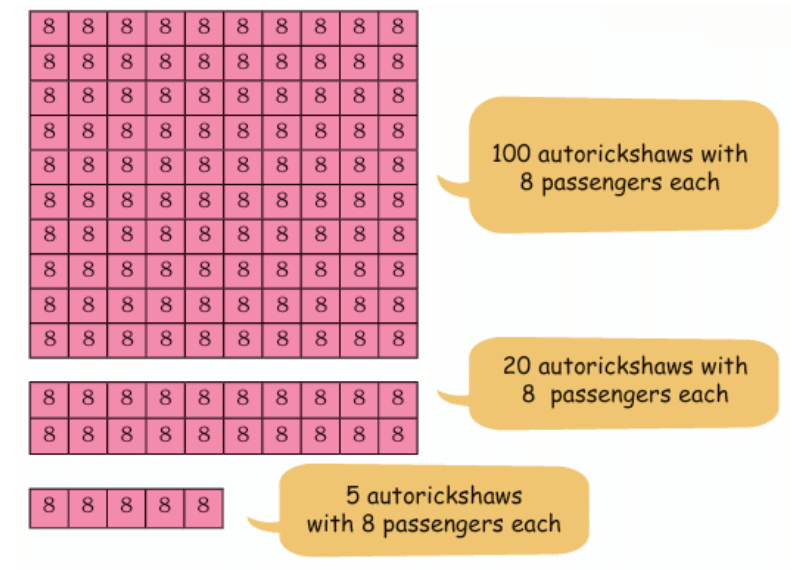

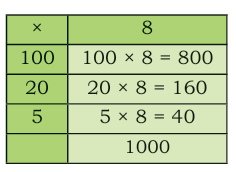• 100 autos × 8 passengers = 800 passengers
• 20 autos × 8 passengers = 160 passengers
• 5 autos × 8 passengers = 40 passengers

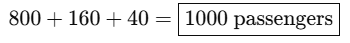
125 electric autorickshaws can carry 1000 people in a single round! 

2. Kahlu and Rabia are potters and make earthen pots   (kulhad) for trains. They pack 6 kulhads in a box and have packed 174 boxes for delivery. How many kulhads have they made? The total number of kulhads is ________.

Sol: Split 174 into parts:

• 100 boxes

• 70 boxes

• 4 boxes

Each box has 6 kulhads.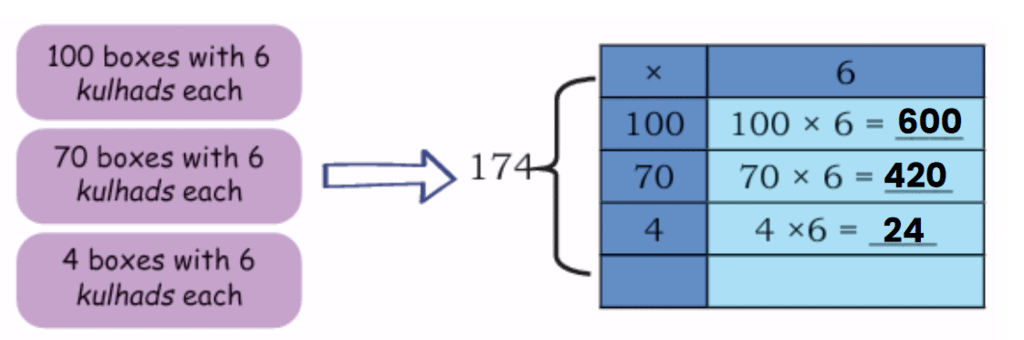

• 100 × 6 = 600 kulhads
• 70 × 6 = 420 kulhads
• 4 × 6 = 24 kulhads

Kahlu and Rabia have made 1044 kulhads in total!

More Division

Imagine there are 108 people standing near a river. They all want to cross the river using 9 boats. Each boat must carry the same number of people. So, the question is: How many people should sit in each boat?

Ans: 108 people need to go in 9 boats.

To find out how many people in 1 boat, we divide:

1. Suppose we put 5 people in each boat.

   • 5 × 9 = 45 people are now sitting.

2. But 108 is a much bigger number.
   So we add 5 more people to each boat (5 + 5 = 10 people in each boat).

   • 10 × 9 = 90 people are now sitting.

3. Still, some people are left!

   • 108 - 90 = 18 people are still waiting.

4. We now share the 18 people among the 9 boats.

   • 18 ÷ 9 = 2 more people for each boat.

5. So, now each boat will carry:

   • 10 + 2 = 12 people.

Patterns in Division

 Imagine you and your two friends (total 3 children) get some money, and you have to share it equally.

• ₹30 shared equally among 3 children:

  • 30 ÷ 3 = 10

  • Each child gets ₹10.

• ₹900 shared equally among 3 children:

  • 900 ÷ 3 = 300

  • Each child gets ₹300.

Some Solved Examples

Example 1: What are the first 5 multiples of 7?

Sol: We multiply 7 by 1, 2, 3, 4, and 5.

7 x 1 = 7

7 x 2 = 14

7 x 3 = 21

7 x 4 = 28

7 x 5 = 35

The first 5 multiples of 7 are 7, 14, 21, 28, and 35.

Example 2: Find the first two common multiples of 2 and 5.

Sol: Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, ...

Multiples of 5: 5, 10, 15, 20, 25, 30, ...

The numbers that appear in both lists are the common multiples.

The first two common multiples of 2 and 5 are 10 and 20.

Example 3: Calculate 42 x 6.

Sol: Break down 42 into 40 + 2.

Multiply each part by 6:

40 x 6 = 240

2 x 6 = 12

Add the results: 240 + 12 = 252

 42 x 6 = 252.