Grade 9 Exam > Grade 9 Notes > Calculus AB > Chapter Notes: Estimating Derivatives of a Function at a Point
Estimating Derivatives of a Function at a Point Chapter Notes | Calculus AB - Grade 9 PDF Download
| Table of contents |
|
| Understanding Derivatives |
|
| Methods for Estimating Derivatives |
|
| Estimating Derivatives by Hand |
|
| Estimating Derivatives with Technology |
|
Understanding Derivatives
A derivative measures how a function changes at a given point, essentially capturing the instantaneous rate of change. When we estimate a derivative, we’re approximating this rate at a specific point, denoted as f'(x) or f'(a), where x or a is the point of interest. To get a precise estimate, we use a small interval around that point—the smaller the interval, the better the approximation.
Methods for Estimating Derivatives
There are three main approaches to estimate derivatives:
- By Hand: Using the limit definition of a derivative to approximate the rate of change.
- Graphically: Drawing a tangent line at the point on the function’s graph and estimating its slope.
- Using Technology: Leveraging tools like graphing calculators or software such as Desmos for quick calculations.
In practice, you’ll often combine manual calculations with technology. Let’s explore these methods with examples.
Estimating Derivatives by Hand
To estimate a derivative manually, we calculate the slope between two points close to the target point, using the difference quotient formula:
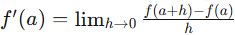This formula approximates the derivative by finding the slope over a tiny interval, as h approaches zero. Let’s apply this to a real-world problem from the 2021 AP Calculus AB exam (credit to College Board).[Intext Question]
Example: Bacteria Density in a Petri Dish
A bacteria population’s density in a circular petri dish, measured in milligrams per square centimeter, is given by a differentiable, increasing function f(r), where r is the distance in centimeters from the dish’s center. A table provides f(r) values for specific r values (data courtesy of College Board).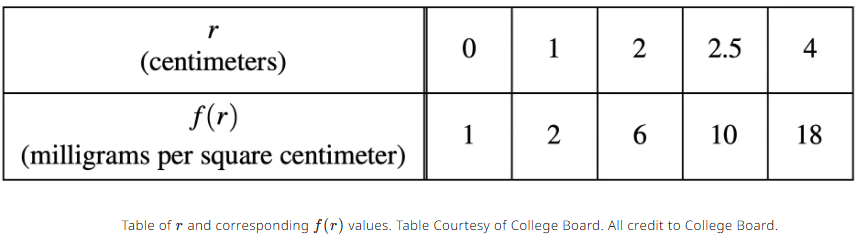
Use the data in the table to estimate f′(2.25). Using correct units, interpret the meaning of your answer in the context of this problem.
Step 1: Estimating f'(2.25)
Remember that a derivative can be found using this definition: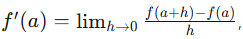 
where we are calculating the slope between two points close to one another.
In this case, the best points to use would be (2, 6)and (2.5, 10) because they are an equal distance away from the point r = 2.25.
Therefore, you can estimate f′(2.5) with the following: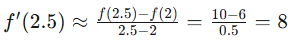
b) Interpreting f′(2.25)
When you interpret data, you have to put the math into context of the question, which in this case, is the density of bacteria.
When the radius of the petri dish is 2.25 centimeters, the density of bacteria, in milligrams per square centimeter, will be increasing by 8 milligrams per square centimeter per centimeter.
The above answers would accumulate 2/2 points for this part of the FRQ!
Estimating Derivatives with Technology
Technology simplifies derivative estimation, especially for complex functions. Graphing calculators like the TI-Nspire or online tools like Desmos can compute derivatives quickly. Let’s see how to estimate a derivative using both.
Example: Derivative of a Trigonometric Function
Estimate the derivative of f(x) =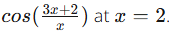 
Using a graphing calculator is the fastest way to calculate f′(x) in this scenario.
For the TI-Nspire specifically, you can go to Menu > Calculus > Numerical Derivative at a Point. Make sure your calculator is set to radian mode!
Since the dependent variable of this function is x, we must take the derivative with respect to x. The value we are trying to calculate at is 2, and we are calculating only the first derivative. Then you can plug in the expression for f(x), and your function should look similar to this: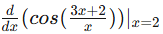
When you press enter, the calculator will give you the value of −0.378401.
So f′(2) = −0.378401.
Estimating Derivatives with Desmos
Now let’s attempt this question with Desmos. First, input the function into the Desmos calculator as f(x) =
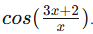Then, you can simply type f′(2) and Desmos will calculate the value for you! You should get that f′(2) = −0.378401247654. Looking at the graph, we can guess that f′(2) should be negative, since the function f(x) is decreasing at x = 2, so we should have everything calculated correctly.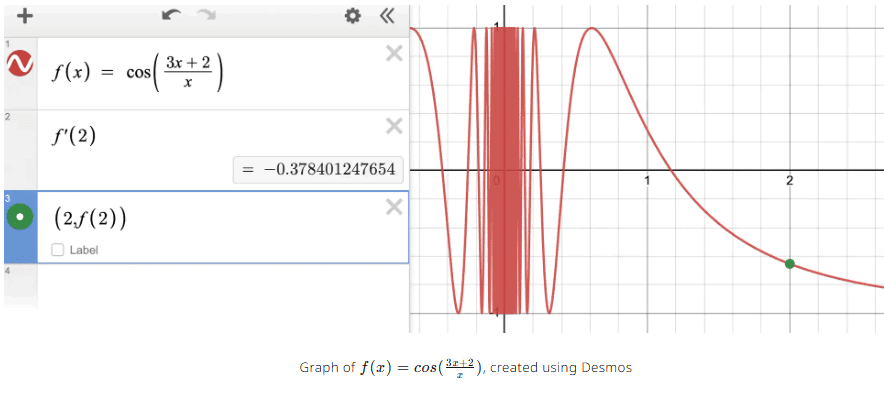
[Intext Question]
Key Terms to Know
- Calculator: An electronic device for performing mathematical operations, from basic arithmetic to advanced functions.
- Computer Software: Programs and instructions that enable computers to perform tasks, including system and application software.
- Difference Quotient: A formula that calculates the average rate of change between two points on a graph, divided by their x-value difference.
- Estimating Derivatives: Approximating a function’s derivative at a point when exact computation is challenging.
- Function: A relation where each input (domain) maps to exactly one output (range).
- Rate of Change: The ratio of change in one variable relative to another, measuring how quickly a quantity changes.
- Slope: A measure of a line’s steepness, calculated as the rise over the run.
- Tangent Line: A line that touches a curve at one point without crossing it, used to approximate instantaneous rates of change.
The document Estimating Derivatives of a Function at a Point Chapter Notes | Calculus AB - Grade 9 is a part of the Grade 9 Course Calculus AB.
All you need of Grade 9 at this link: Grade 9
|
26 videos|75 docs|38 tests
|
FAQs on Estimating Derivatives of a Function at a Point Chapter Notes - Calculus AB - Grade 9
| 1. What is a derivative and why is it important in mathematics? |  |
Ans.A derivative represents the rate of change of a function at a given point. It is important because it helps us understand how a function behaves, allowing us to analyze trends, optimize values, and solve real-world problems related to motion, growth, and decay.
| 2. How can I estimate the derivative of a function by hand? | |
Ans.To estimate the derivative of a function by hand, you can use the definition of the derivative, which involves calculating the limit of the average rate of change as the interval approaches zero. This usually involves finding the difference quotient (f(x+h) - f(x))/h and evaluating it as h approaches zero.
| 3. What technology tools can I use to estimate derivatives effectively? | |
Ans.You can use graphing calculators, computer software like Desmos or GeoGebra, and programming languages like Python with libraries such as NumPy and Matplotlib. These tools can help visualize functions and calculate derivatives more efficiently than manual methods.
| 4. How do I interpret the value of a derivative at a specific point? | |
Ans.The value of a derivative at a specific point indicates the slope of the tangent line to the function at that point. A positive derivative means the function is increasing, while a negative derivative indicates it is decreasing. A zero derivative suggests a possible maximum, minimum, or inflection point.
| 5. Can derivatives be estimated for non-linear functions? | |
Ans.Yes, derivatives can be estimated for non-linear functions. In fact, many functions are non-linear, and the process of estimating their derivatives is essential for understanding their behavior. The same methods, both by hand and with technology, can be applied to non-linear functions as well.
About this Document
Oct 05, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Estimating Derivatives of a Function at a Point for Grade 9 2025 is part of Calculus AB preparation.
The notes and questions for Chapter Notes: Estimating Derivatives of a Function at a Point have been prepared according to the Grade 9 exam syllabus. Information about Chapter Notes: Estimating Derivatives of a Function at a Point covers topics
like Understanding Derivatives, Methods for Estimating Derivatives, Estimating Derivatives by Hand, Estimating Derivatives with Technology and Chapter Notes: Estimating Derivatives of a Function at a Point Example, for Grade 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Estimating Derivatives of a Function at a Point.
Introduction of Chapter Notes: Estimating Derivatives of a Function at a Point in English is available as part of our Calculus AB
for Grade 9 & Chapter Notes: Estimating Derivatives of a Function at a Point in Hindi for Calculus AB course.
Download more important topics related with notes, lectures and mock test series for Grade 9
Exam by signing up for free. Grade 9: Estimating Derivatives of a Function at a Point Chapter Notes | Calculus AB - Grade 9
Description
Full syllabus notes, lecture & questions for Estimating Derivatives of a Function at a Point Chapter Notes | Calculus AB - Grade 9 - Grade 9 | Plus excerises question with solution to help you revise complete syllabus for Calculus AB | Best notes, free PDF download
Information about Chapter Notes: Estimating Derivatives of a Function at a Point
In this doc you can find the meaning of Chapter Notes: Estimating Derivatives of a Function at a Point defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Estimating Derivatives of a Function at a Point theory, EduRev gives you an ample number of questions to practice Chapter Notes: Estimating Derivatives of a Function at a Point tests, examples and also practice Grade 9
tests
Related Searches
past year papers
,Summary
,Previous Year Questions with Solutions
,Estimating Derivatives of a Function at a Point Chapter Notes | Calculus AB - Grade 9
,Viva Questions
,ppt
,practice quizzes
,Extra Questions
,study material
,Estimating Derivatives of a Function at a Point Chapter Notes | Calculus AB - Grade 9
,Sample Paper
,shortcuts and tricks
,Exam
,Free
,Important questions
,Estimating Derivatives of a Function at a Point Chapter Notes | Calculus AB - Grade 9
,video lectures
,MCQs
,mock tests for examination
,Semester Notes
,Objective type Questions
;
Additional Information about Chapter Notes: Estimating Derivatives of a Function at a Point for Grade 9 Preparation
Chapter Notes: Estimating Derivatives of a Function at a Point Free PDF Download
The Chapter Notes: Estimating Derivatives of a Function at a Point is an invaluable resource that delves deep into the core of the Grade 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Estimating Derivatives of a Function at a Point now and kickstart your journey towards success in the Grade 9 exam.
Importance of Chapter Notes: Estimating Derivatives of a Function at a Point
The importance of Chapter Notes: Estimating Derivatives of a Function at a Point cannot be overstated, especially for Grade 9 aspirants.
This document holds the key to success in the Grade 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Estimating Derivatives of a Function at a Point
Chapter Notes: Estimating Derivatives of a Function at a Point Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Estimating Derivatives of a Function at a Point.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Estimating Derivatives of a Function at a Point Notes on EduRev are your ultimate resource for success.
Chapter Notes: Estimating Derivatives of a Function at a Point Grade 9 Questions
The "Chapter Notes: Estimating Derivatives of a Function at a Point Grade 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Grade 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Estimating Derivatives of a Function at a Point on the App
Students of Grade 9 can study Chapter Notes: Estimating Derivatives of a Function at a Point alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Estimating Derivatives of a Function at a Point,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Estimating Derivatives of a Function at a Point is prepared as per the latest Grade 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup