Factors and Multiples Chapter Notes | Mathematics for Grade 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Factors |

|
| Greatest common factor |

|
| Multiples |

|
| Least common multiple |

|
Introduction
Factors and multiples are key math concepts for understanding numbers. Factors are numbers you multiply to get a specific number, like 1, 2, 4, and 8 for 8. Multiples are the results of multiplying a number by whole numbers, like 3, 6, 9 for 3. The greatest common factor (GCF) is the largest number two numbers share, useful for simplifying fractions. The least common multiple (LCM) is the smallest number two numbers both divide into, helpful for adding fractions.
Factors
What are factors?
- Factors are numbers you multiply together to get another number.
- For example, what are the factors of the number 8? Think about all of the whole numbers you can multiply to get 8.
1 × 8 = 8
2 × 4 = 8
So, the factors of 8 are 1, 2, 4, and 8. - A factor of a number divides the number evenly, with no remainder.
How do you find all the factors of a number?
You can use factor pairs to find all the factors of 24. A factor pair consists of two numbers that multiply to give 24. Let’s go step by step.
- Step 1: Start with 1
Multiply 1 × 24 to get 24. So, 1 and 24 are factors of 24.
1 × 24 = 24
Place 1 at the beginning and 24 at the end of the factor list. - Step 2: Try 2
Multiply 2 × 12 to get 24.
2 × 12 = 24
Add 2 and 12 to the factor list. - Step 3: Try 3
Multiply 3 × 8 to get 24.
3 × 8 = 24
Add 3 and 8 to the factor list. - Step 4: Try 4
Multiply 4 × 6 to get 24.
4 × 6 = 24
Add 4 and 6 to the factor list. - Step 5: Try 5
The number 24 cannot be divided by 5 evenly, so 5 is not a factor. - Step 6: Check 6 and Beyond
Since 6 is already on the list, we stop here as higher numbers will repeat factor pairs. - Final List of Factors
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
Fun Fact: Every positive whole number has at least 2 factors, 1 and the number itself. If these are the only two factors, the number is a prime number. If there are more than 2 factors, the number is a composite number.
Greatest common factor
What is the greatest common factor?
- The greatest common factor (GCF) of two numbers is the largest factor that the two numbers share. Finding the GCF can help you with other skills, such as simplifying fractions.
- For Example: Let's try it with 16 and 24.
First, find all of the factors of each number:
16: 1, 2, 4, 8, 16
24: 1, 2, 3, 4, 6, 8, 12, 24
Next, look for the common factors. Find the largest one.
16: 1, 2, 4, 8, 16
24: 1, 2, 3, 4, 6, 8, 12, 24
So, the greatest common factor of 16 and 24 is 8!
How can you use the greatest common factor to simplify fractions?
- You can divide the numerator and denominator of a fraction by their GCF to find the simplest form!
- For Example: Let's try it with 16/24.
You know the greatest common factor of 16 and 24 is 8. So, divide both 16 and 24 by 8.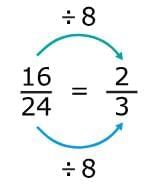 The simplest form of 16/24 is 2/3!
The simplest form of 16/24 is 2/3!
Multiples
What are multiples?
- When you multiply a number by a whole number, you get a multiple of that first number.
- For example, start with 3. If you multiply 3 by 4, you get 12. So, 12 is a multiple of 3.
The number 3 has many multiples. Let's find the first few.
3 × 1 = 3
3 × 2 = 6
3 × 3 = 9
3 × 4 = 12
3 × 5 = 15
So, the first few multiples of 3 are 3, 6, 9, 12, and 15!
Tips
- Every whole number is a multiple of its factors. For example:
- 3 is a factor of 6
- 6 is a multiple of 3
- When you start at a number and skip-count by that number, you are saying its multiples! Try it with 5.
- These are all multiples of 5: 5, 10, 15, 20, 25, ...
Least common multiple
What is the least common multiple?
- The least common multiple (LCM) of two numbers is the smallest multiple that the two numbers have in common. Finding the LCM can help you with other skills, such as finding equivalent fractions with like denominators.
- For Example: Let's try it with 6 and 8.
First, list a few multiples of each number.
6: 6, 12, 18, 24, 30, 36, 42, 48...
8: 8, 16, 24, 32, 40, 48, 56, 64...
Next, look at the common multiples. Find the smallest one.
6: 6, 12, 18, 24, 30, 36, 42, 48...
8: 8, 16, 24, 32, 40, 48, 56, 64...
So, the LCM of 6 and 8 is 24!
Why is the least common multiple useful?
- Let's say you want to add two fractions with different denominators. You'll want to make equivalent fractions that have like denominators. To do that, you can use the least common multiple of the two denominators. This is also known as the least common denominator, or LCD.
- For Example: Let's try it with 1/5 and 3/4.
First, list a few multiples of each denominator. Find the smallest multiple they have in common.
5: 5, 10, 15, 20, 25...
4: 4, 8, 12, 16, 20...
The LCD of 1/5 and 3/4 is 20.
Next, create equivalent fractions using the LCD as the denominator. To make an equivalent fraction, multiply the numerator and denominator by the same number.
For 1/5, multiply the numerator and denominator by 4.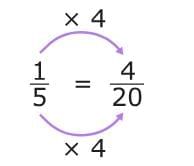 The equivalent fraction is 4/20!
The equivalent fraction is 4/20!
For 3/4, multiply the numerator and denominator by 5. The equivalent fraction is 15/20. Now the fractions have the same denominator, so they're ready for you to add!
The equivalent fraction is 15/20. Now the fractions have the same denominator, so they're ready for you to add!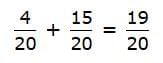
Finding the least common multiple through prime factors
- You can also use prime factorization to find the LCM of two numbers.
- For Example: Let's try it with 20 and 24.
First, write out the prime factorization of each number.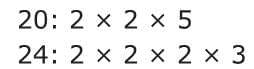 Then, line up any matching prime numbers vertically.
Then, line up any matching prime numbers vertically.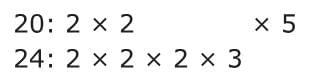 Bring down the prime numbers in each column. The least common multiple is the product of these prime factors.
Bring down the prime numbers in each column. The least common multiple is the product of these prime factors.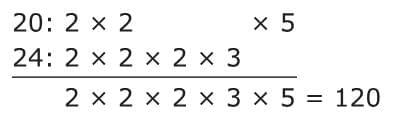 So, the LCM of 20 and 24 is 120!
So, the LCM of 20 and 24 is 120!
|
36 videos|76 docs|14 tests
|
FAQs on Factors and Multiples Chapter Notes - Mathematics for Grade 6
| 1. What are factors, and how do you find them for a given number? |  |
| 2. How do you determine the greatest common factor (GCF) of two numbers? |  |
| 3. What are multiples, and how can you find the first few multiples of a number? |  |
| 4. What is the least common multiple (LCM), and how can you calculate it for two numbers? |  |
| 5. Why are factors and multiples important in mathematics? |  |














