Grade 9 Exam > Grade 9 Notes > Calculus AB > Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions
Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Chapter Notes | Calculus AB - Grade 9 PDF Download
Welcome to your guide for conquering advanced trigonometric derivatives in AP Calculus! If you’ve already nailed the derivatives of sin(x) and cos(x), you’re ready to tackle the rest. Memorizing these rules will make your calculus journey smoother and more intuitive.
Overview of Trigonometric Derivatives
Below is a concise table summarizing the derivatives of tangent, cotangent, secant, and cosecant functions. Note that these derivatives apply only when angles are in radians, not degrees.
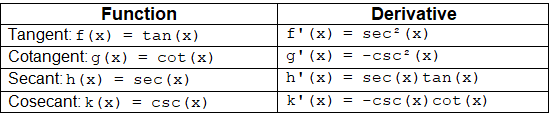
Tip: Familiarize yourself with trigonometric identities like tan(x) = sin(x)/cos(x) and cot(x) = 1/tan(x) to simplify expressions before differentiating.
Derivative of tan(x)
The derivative of tan(x) is sec²(x). Let’s explore an example:
Consider the function: f(x) = 3tan(x) + 2x²
Differentiate each term separately:
- For 3tan(x), the derivative is 3sec²(x).
- For 2x², the derivative is 4x.
Thus, the derivative is: f'(x) = 3sec²(x) + 4x.
Derivative of cot(x)
The derivative of cot(x) is -csc²(x). Here’s an example:
Given: f(x) = 5cot(x) + x
We again have to differentiate the two terms separately! The derivative of cot x is −csc2x, so the derivative of the first term is −5csc2x. The derivative of x is 1. Therefore, f′(x)=−5csc2x + 1 or f′(x) = 1 − 5csc2x.
Derivative of sec(x)
The derivative of sec(x) is sec(x)tan(x). For example:
Take: f(x) = 2sec(x) + 3x³
Knowing the above trig derivative rule, the derivative of the first term is 2secx tanx. The derivative of 3x3 is 9x2. Thus, f′(x) = 2secx tanx + 9x2.
Derivative of csc(x)
The derivative of csc(x) is -csc(x)cot(x). Here’s an example:
Consider: f(x) = 4csc(x) + 7x²
Differentiate each part:
- The derivative of 4csc(x) is -4csc(x)cot(x).
- The derivative of 7x² is 14x.
Therefore: f'(x) = -4csc(x)cot(x) + 14x.
Practice Problems
Test your understanding with these practice questions. Apply the chain rule, sum rule, and quotient rule where necessary.
- f(x) = 2tan(x) + sec(x)
- f(x) = cot(x)/csc(x)
- g(x) = tan²(6x)
- h(x) = 5cot(x)
Solutions
- f'(x) = 2sec²(x) + sec(x)tan(x)
- f'(x) = -csc²(x)
- g'(x) = 2tan(6x)(1/cos²(6x))
- h'(x) = -5csc²(x)
These problems integrate multiple derivative rules. If you need a refresher, review the power rule, sum/difference rules, product rule, quotient rule, and derivatives of basic functions like sin(x), cos(x), ex, and ln(x).
Question for Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant FunctionsTry yourself: What is the derivative of tan(x)?View Solution
Key Terms to Understand
- Chain Rule: A method for differentiating composite functions, multiplying the derivative of the outer function by the derivative of the inner function.
- Cotangent: A trigonometric ratio defined as the adjacent side over the opposite side in a right triangle.
- (cot(x))': The derivative of the cotangent function, indicating its rate of change.
- -csc²(x): The derivative of the cosecant function squared, with a negative sign.
- -csc(x)cot(x): The product of cosecant and cotangent functions, negated, used in derivative calculations.
- Derivatives: Measures of how a function changes as its input varies.
- sec²(x): The derivative of the secant function, representing its rate of change.
- Secant: A trigonometric ratio defined as the hypotenuse over the adjacent side in a right triangle.
- sec(x)': The derivative of the secant function, showing its rate of change.
- Tangent: A line that touches a curve at one point, sharing the same slope as the curve at that point.
The document Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Chapter Notes | Calculus AB - Grade 9 is a part of the Grade 9 Course Calculus AB.
All you need of Grade 9 at this link: Grade 9
|
26 videos|75 docs|38 tests
|
FAQs on Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Chapter Notes - Calculus AB - Grade 9
| 1. What are the basic derivatives of trigonometric functions? |  |
Ans. The basic derivatives of trigonometric functions are as follows:
- The derivative of sin(x) is cos(x).
- The derivative of cos(x) is -sin(x).
- The derivative of tan(x) is sec^2(x).
- The derivative of cot(x) is -csc^2(x).
- The derivative of sec(x) is sec(x)tan(x).
- The derivative of csc(x) is -csc(x)cot(x).
| 2. How do you find the derivative of the tangent function? | |
Ans. To find the derivative of the tangent function, you use the formula:
The derivative of tan(x) is sec^2(x). This can be derived from the quotient rule since tan(x) is sin(x)/cos(x), or you can memorize this derivative as a key trigonometric derivative.
| 3. What is the derivative of cotangent, and how is it derived? | |
Ans. The derivative of cotangent is -csc^2(x). This can be derived by applying the quotient rule to cot(x) = cos(x)/sin(x), which results in the derivative being -csc^2(x) after simplification.
| 4. Can you explain how to differentiate secant and cosecant functions? | |
Ans. Yes! The derivative of sec(x) is sec(x)tan(x), which can be understood by applying the product rule and the chain rule. For cosecant, the derivative is -csc(x)cot(x), which is also derived using the quotient rule.
| 5. Why are trigonometric derivatives important in calculus? | |
Ans. Trigonometric derivatives are important in calculus because they help in solving problems involving rates of change, optimization, and modeling periodic phenomena. They are essential in higher-level mathematics and physics, where understanding the behavior of trigonometric functions is crucial.
About this Document
Oct 05, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions for Grade 9 2025 is part of Calculus AB preparation.
The notes and questions for Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions have been prepared according to the Grade 9 exam syllabus. Information about Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions covers topics
like Overview of Trigonometric Derivatives, Practice Problems and Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Example, for Grade 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions.
Introduction of Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions in English is available as part of our Calculus AB
for Grade 9 & Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions in Hindi for Calculus AB course.
Download more important topics related with notes, lectures and mock test series for Grade 9
Exam by signing up for free. Grade 9: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Chapter Notes | Calculus AB - Grade 9
Description
Full syllabus notes, lecture & questions for Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Chapter Notes | Calculus AB - Grade 9 - Grade 9 | Plus excerises question with solution to help you revise complete syllabus for Calculus AB | Best notes, free PDF download
Information about Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions
In this doc you can find the meaning of Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions theory, EduRev gives you an ample number of questions to practice Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions tests, examples and also practice Grade 9
tests
Related Searches
and/or Cosecant Functions Chapter Notes | Calculus AB - Grade 9
,study material
,practice quizzes
,video lectures
,Cotangent
,Finding the Derivatives of Tangent
,Secant
,Sample Paper
,Previous Year Questions with Solutions
,Extra Questions
,Objective type Questions
,Cotangent
,mock tests for examination
,shortcuts and tricks
,Summary
,Cotangent
,Important questions
,Finding the Derivatives of Tangent
,and/or Cosecant Functions Chapter Notes | Calculus AB - Grade 9
,Free
,ppt
,past year papers
,Semester Notes
,Secant
,MCQs
,Finding the Derivatives of Tangent
,Exam
,Secant
,and/or Cosecant Functions Chapter Notes | Calculus AB - Grade 9
,Viva Questions
;
Additional Information about Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions for Grade 9 Preparation
Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Free PDF Download
The Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions is an invaluable resource that delves deep into the core of the Grade 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions now and kickstart your journey towards success in the Grade 9 exam.
Importance of Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions
The importance of Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions cannot be overstated, especially for Grade 9 aspirants.
This document holds the key to success in the Grade 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions
Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Notes on EduRev are your ultimate resource for success.
Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Grade 9 Questions
The "Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions Grade 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Grade 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions on the App
Students of Grade 9 can study Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions is prepared as per the latest Grade 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup