Fractions Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
Introduction to Fractions
A fraction is a way of representing a part of a whole.
When a complete item is split into equal sections, each section is known as a fraction of the whole.
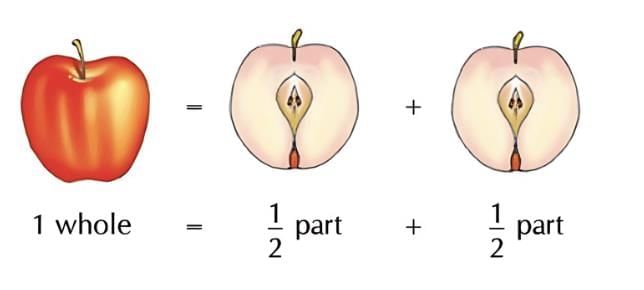 It has two parts:
It has two parts:
Numerator (the top number): shows how many equal parts are taken.
Denominator (the bottom number): shows into how many equal parts the whole is divided.

Comparison of Fractions with Different Denominators
Fractions only make sense when we know what the whole is.
Two fractions like and can be directly compared only if they come from the same whole.
This means that when fractions have different denominators, you cannot compare them directly. To make them comparable, we convert them into equivalent fractions with the same denominator.
Let's understand this using an example
Tamanna is a fifth-grade student. She has two chocolates of different sizes
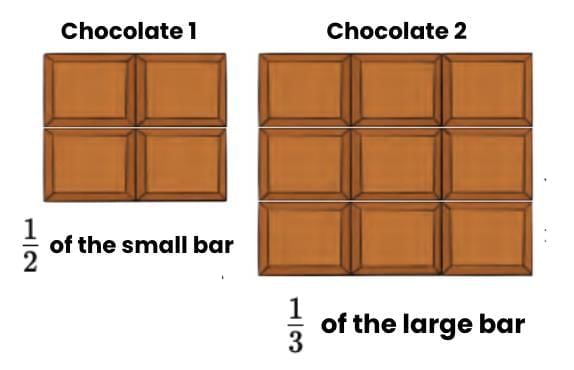
She says that: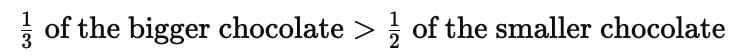
We can see that chocolate 2 is a lot bigger than chocolate 1; they are of different sizes, so we can't really compare them.
Let's learn about the rule for comparing fractions!
To compare fractions correctly:
The whole must be the same.
Example: Compare and of the same chocolate. Here, is always bigger.
But if the wholes are different, the result depends on the size of the wholes.
Therefore, before comparing fractions, make sure they are taken from the same whole object.
Playing with a Grid
Fractions can sometimes feel tricky, but grids make them easy to see and understand.
By shading parts of a grid, we can visualise how much of a whole a fraction represents.
What is a grid?
A grid is divided into equal parts (like boxes in a chocolate bar).
 Grid A
Grid AEach small box represents one equal part of the whole.
When we shade some parts, we show a fraction of the total.
Example 1: Shade 1/3 on the grid A red
Divide a grid into 3 equal parts.
Shade 1 out of 3 parts.
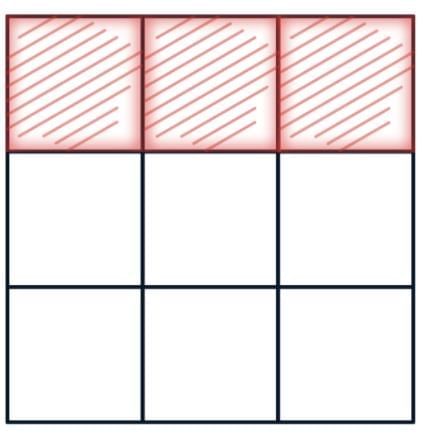
This shows 1/3, or “one-third of the whole.”
Example 2: Shade 2/3 on the grid A black
Divide a grid into 3 equal parts.
Shade 2 out of 3 parts.

This shows 2/3, or “two-thirds of the whole.”
Understanding Equivalent Fractions
These are fractions that represent the same value or part of a whole, even though they have different numerators and denominators.
For example: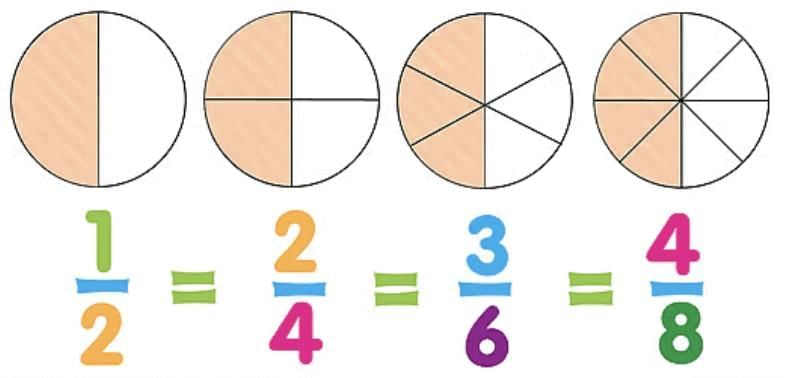
Let's Check!
Look at the grid below. The grid is divided into 6 equal parts.

Is 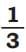 equal to
equal to 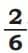 ? Explain using the shaded parts.
? Explain using the shaded parts.
Solution:
Step 1: Shade 2 out of 6 parts of the grid

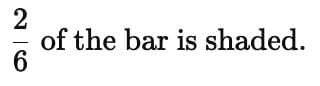
Step 2: Now, let’s divide the same grid into 3 equal parts.
Step 3: Shade 1 out of 3 parts of the grid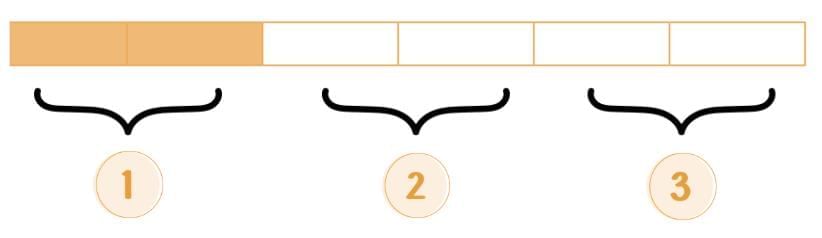
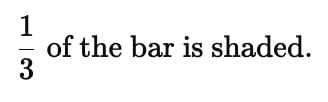
Now, compare the shaded regions. In both cases, the same amount of the bar is shaded.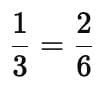
Fractions that represent the same portion of a whole are called Equivalent Fractions.
Fun with Fraction Kit
Using a fraction kit helps us understand how fractions work. A fraction kit contains strips divided into equal parts.
A whole can be divided into many equal parts: halves, thirds, fourths, fifths, sixths, etc.
The denominator tells us how many equal parts the whole is divided into.
Adding all the equal parts together gives 1 whole
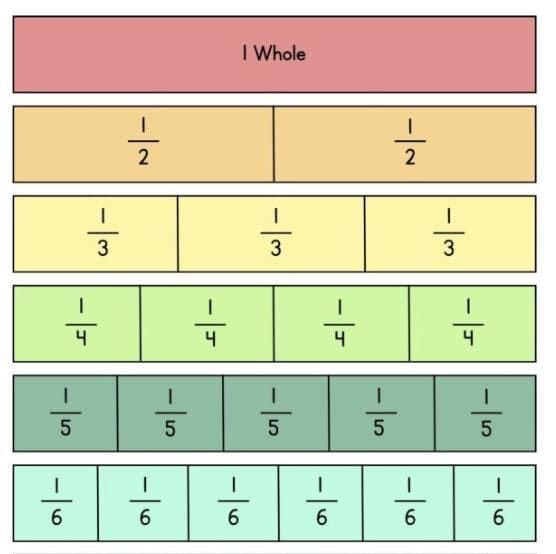
Making a Whole with Fractions
A whole can be made using smaller fraction pieces.
Example: If we use pieces, we need 5 pieces to make 1 whole.

Combining Different Fraction Pieces
Sometimes, we can use different fractions together to form a whole.
- Example: One piece of 1/2 and two pieces of 1/4 make a whole

This shows us:
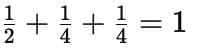
A half () can be divided into two quarters ().
Therefore,
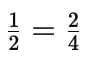 (equivalent fractions)
(equivalent fractions)
Making Equivalent Fractions
To make equivalent fractions, we change the numerator (top number) and denominator (bottom number) in the same way.
This is done by multiplying or dividing both by the same number.
1. Using Multiplication
If we multiply the numerator and denominator of a fraction by the same number, the fraction’s value does not change.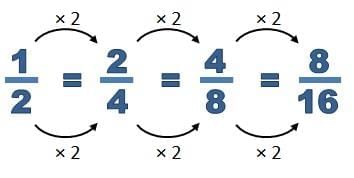
2. Using Division (Simplifying)
If the numerator and denominator have a common factor, we can divide both by the same number.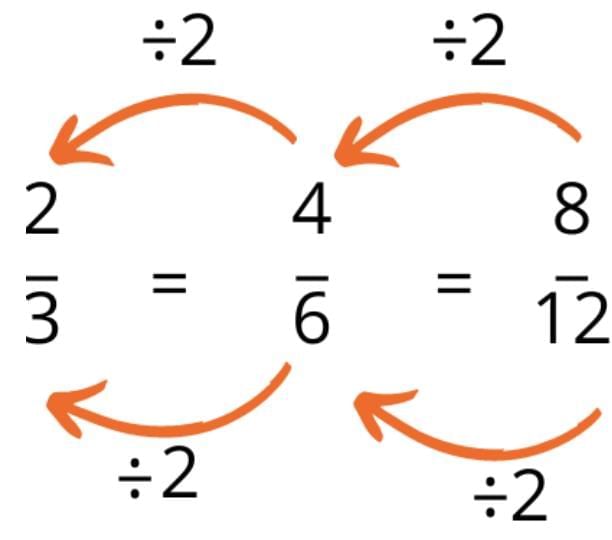
Sameer Discovers Equivalent Fractions
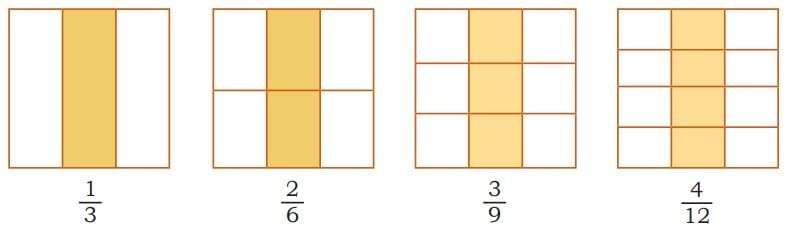
Sameer shaded one-third (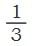 ) of some shapes.
) of some shapes.
Case 1: When he split the shapes into smaller equal parts by drawing lines, he found fractions like:
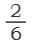 ,
,  ,
,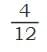 – all exactly cover the same shaded area as 1/3.
– all exactly cover the same shaded area as 1/3.
This means
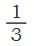 =
= 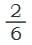 =
= 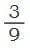 =
= 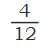
These are equivalent fractions.
Example: Write the next 4 fractions equivalent to 2/5.
 View Answer
View Answer 
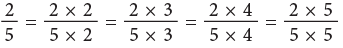
that is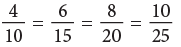
Hence, the next four fractions are equivalent to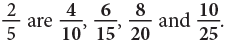
Comparing Fractions—Same Denominator
Fractions have two parts: numerator (top number) and denominator (bottom number).
When fractions have the same denominator, it means the whole is divided into the same number of equal parts.
To compare such fractions, we only need to look at the numerators.
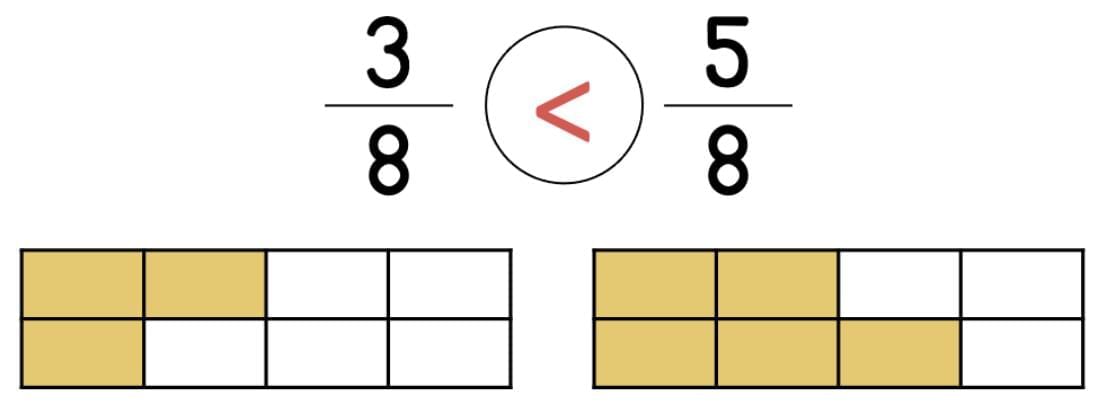
In such cases, the fraction with the larger numerator is the greater fraction.
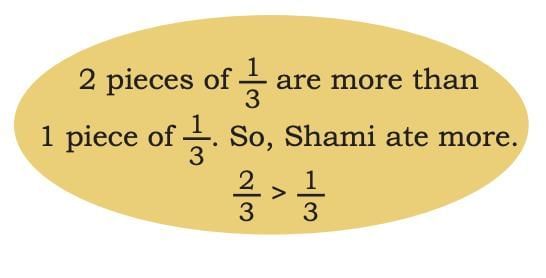
Example: Sevi and Shami divided a piece of chikki between themselves. Sevi ate and Shami ate the rest, that is, . Who ate more?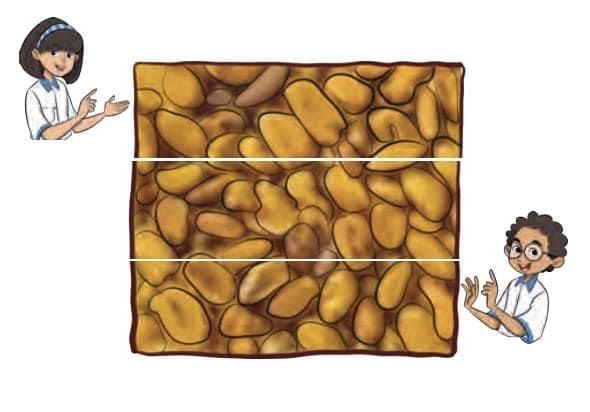
The whole chikki is divided into 3 equal parts (so the denominator is 3).
Sevi ate 1 part →
Shami ate 2 parts →
Since the denominators are the same (3), we only need to compare the numerators.
Numerator for Sevi = 1
Numerator for Shami = 2
Clearly, 2 > 1.
Comparing Fractions – Same Numerator
When fractions have the same numerator (same number of parts), but different denominators (different total parts), the bigger fraction is the one with the smaller denominator.
This is because smaller parts make each piece bigger.
Example: Between Sevi and Shami, can you tell who ate more?
Rule: When numerators are the same, the fraction with the smaller denominator is bigger.
Comparing who ate more paratha

Fractions Greater Than 1
We know, a fraction tells us how many parts of a whole we have.
Let’s take an example. For instance, if a paratha (a soft flatbread) is cut into equal parts:
(one-half) means the paratha is cut into 2 equal parts, and you have one of those parts.
(one-fourth or a quarter) means the paratha is cut into 4 equal parts, and you have one of those parts.
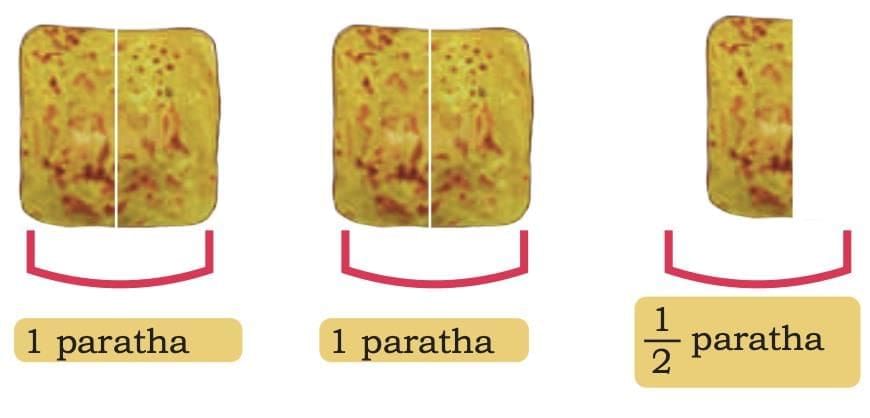
Sometimes, you can eat more than one whole paratha. This happens when you eat many pieces of paratha, so the total amount is more than one whole.
This is called a "fraction greater than 1."
Let’s see this with some examples.
Example 1: Imagine Raman’s father cuts each paratha into halves, that is, 2 equal parts.
If Maa took 5 pieces of paratha, how many whole parathas did she eat?
Since 2 halves make 1 whole paratha.

Then 5 halves are:
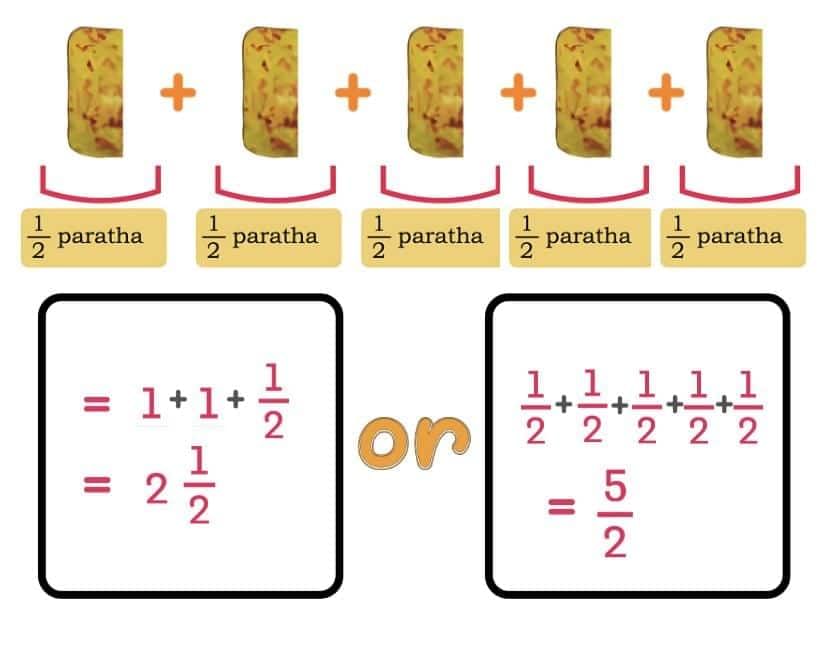
So, Maa ate 2 and a half parathas.
Let's Use a Number Line to Understand
If you draw a line and divide the space between 0 and 1 into 2 equal parts (because halves),
Then each part is .
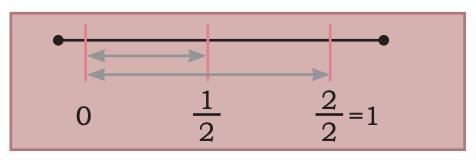
Moving 5 steps of along the line gets you to 2 and .

Let's check Radhika’s halves
Radhika took 6 pieces of parathas.

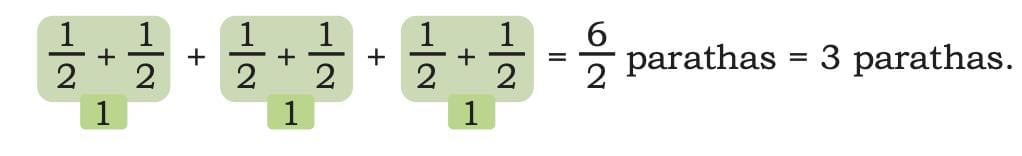
Example 2: Now imagine some day, all parathas were cut into 4 pieces each (fourths).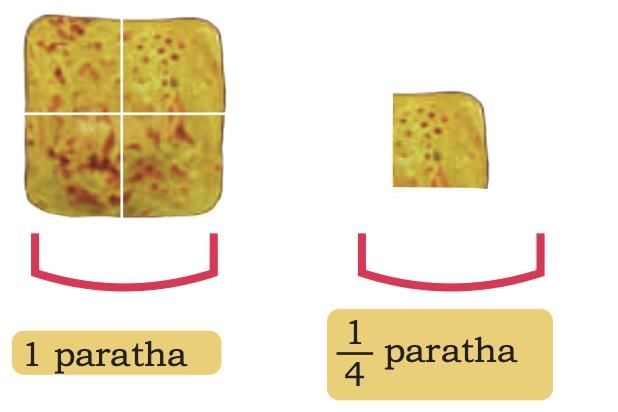
Dadaji took 9 pieces of paratha.
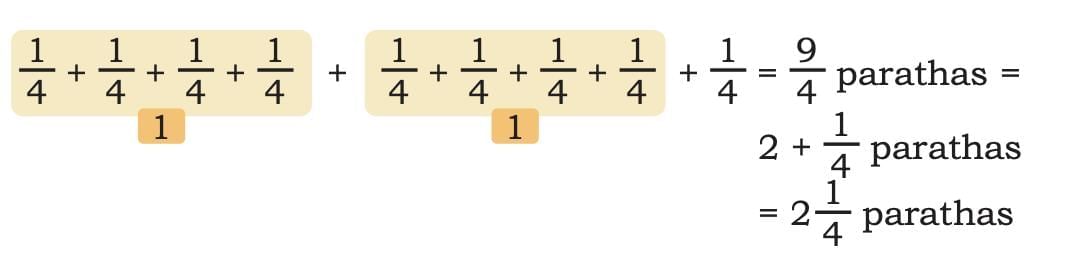
So, he ate 2 and one-fourth parathas.
Example 4: Sharing Pizzas
The family ordered 2 pizzas, and each pizza is cut into 3 equal slices.
Total slices = 2 pizzas × 3 slices = 6 slices
6 family members need 1 slice each.
Dadiji and Dadaji gave their slices to Raman.
Maa and Baba gave theirs to Radhika.
That means:
Each slice is:
(one slice out of 3)
Calculating Raman's Share
Raman gets his slice + 2 slices from Dadiji and Dadaji = 3 slices
Raman’s total pizza = 1
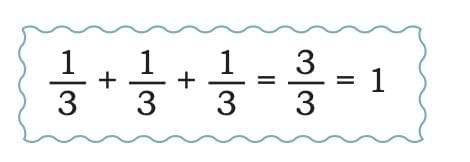
Representation on the number line:

Therefore,

Now Raman couldn't finish and was left with one slice, so he gave it to Radhika
Calculating Radhika's Share
Radhika gets her slice + 2 slices from Maa and Baba + 1 slice from Raman = 4 slices
Radhika’s total pizza = 1
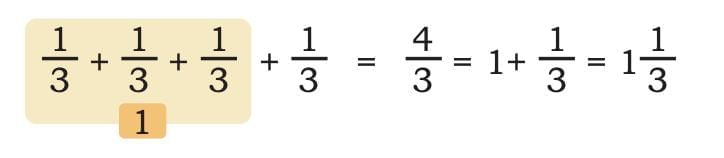
Representation on the number line:
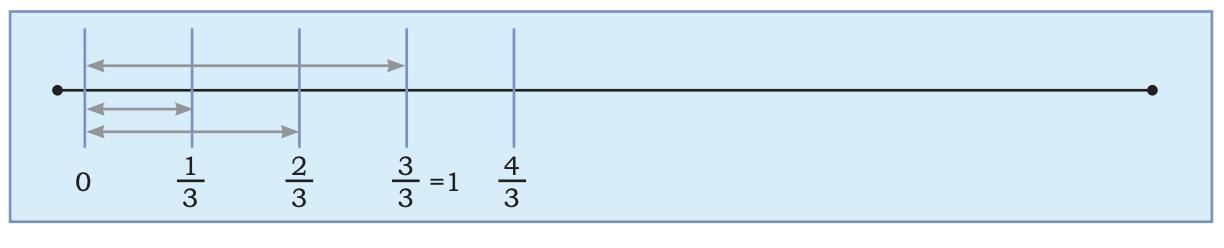
Therefore,
Comparing Fractions With Reference to 1
When comparing fractions, check whether they are less than 1 or greater than 1.
Improper fractions (like ) are always more than 1 whole.
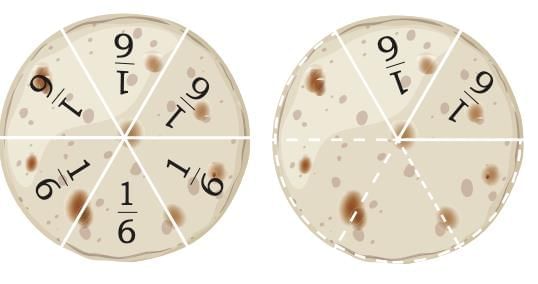
Let us compare some more fractions. Between Sevi and Shami, can you tell who ate less?
Sevi says: “I ate paratha yesterday evening.”
Sami says: “I ate paratha yesterday evening.”
Let’s take a closer look.
means 7 out of 8 equal pieces → this is less than 1 whole paratha.

means 8 out of 6 equal pieces → this is more than 1 whole paratha (since 6 parts make 1 paratha, and 2 parts are extra).
On comparing, we get 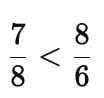
The Sami ate more paratha than the Sevi.
Comparing Fractions with Reference to 1/2
Fractions can often be compared by relating them to , 1, or other simple benchmarks.
Here, we will use as a reference to decide which fraction is greater.

Who do you think ate more paratha?
The Sevi says: “I ate paratha yesterday evening.”

The Sami says: “I ate paratha yesterday evening.”

Let’s take a closer look.
1 means half of the whole.
(since 3 parts out of 6 equal parts = half).
is more than half (because 4 out of 8 parts = half, and here 5 parts are taken).
Therefore, 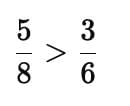
|
35 videos|276 docs|7 tests
|
FAQs on Fractions Chapter Notes - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What are equivalent fractions and how can they be identified? |  |
| 2. How can I compare fractions with the same denominator? |  |
| 3. What is the method to compare fractions with the same numerator? |  |
| 4. How do you compare fractions when one is greater than 1? |  |
| 5. What is the significance of comparing fractions with reference to 1? |  |






















