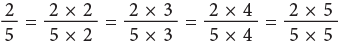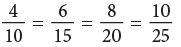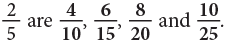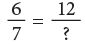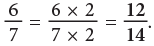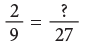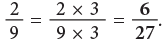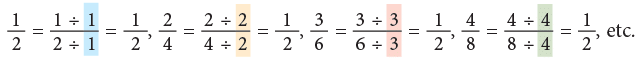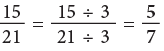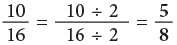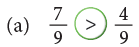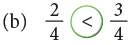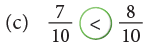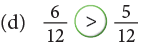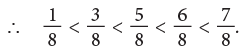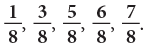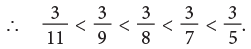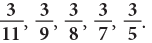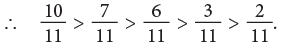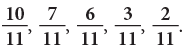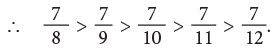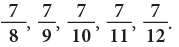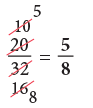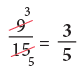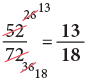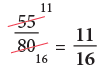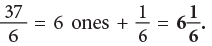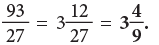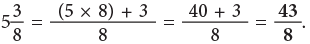Fractions Class 4 Notes Maths
Fraction
A fraction means a part of the whole. The whole can be an object, region or a collection.
When a complete item is split into equal sections, each section is known as a fraction of the whole.
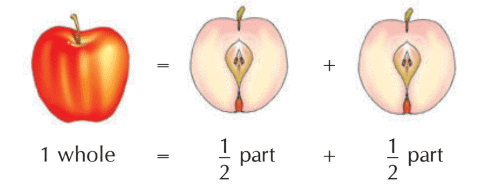
What are fractions?
- The numbers such as half, one-third, one-fourth, two-fifths, five-sixths, etc. are called fractional numbers.
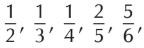 etc., are called fractions.
etc., are called fractions.
1. Fraction as a Part of the Whole
Ankita ordered a pizza for herself.
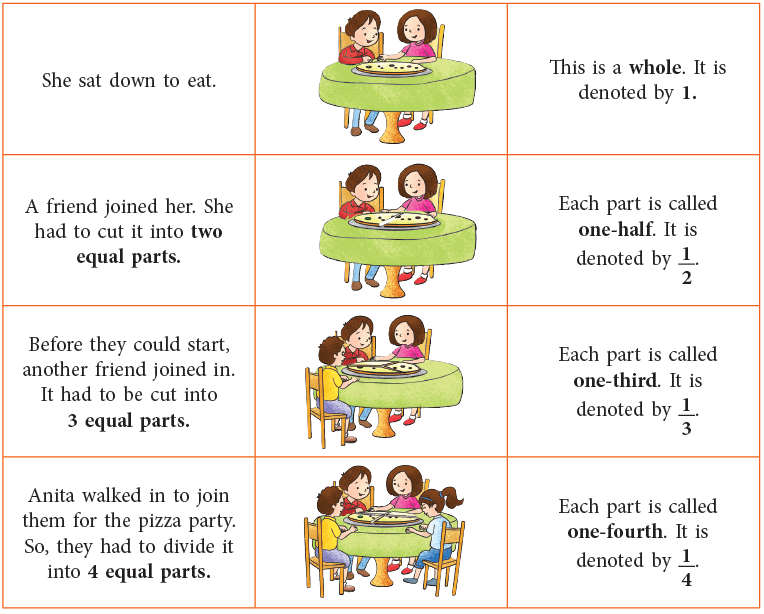 Similarly, we can have more equal parts as under:
Similarly, we can have more equal parts as under:
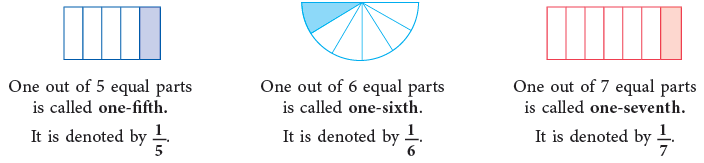 Riya had a loaf of bread which she divided into 3 equal pieces, one for herself and one each for Ritu and Aditi.
Riya had a loaf of bread which she divided into 3 equal pieces, one for herself and one each for Ritu and Aditi.- But Aditi insisted on taking two pieces. Aditi, therefore, got 2 out of 3 equal parts, which is expressed as two-thirds or 2/3 in the language of fractions.
- Similarly, we may define some more fractions as under by colouring the parts.
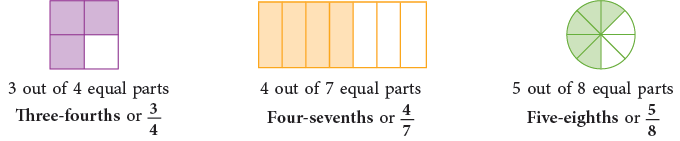
What fraction represents a whole?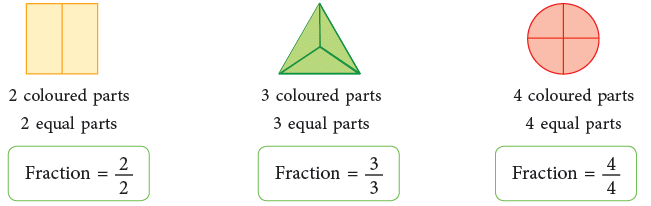 From the above figures, we can clearly see that all parts of a whole figure (expressed as 1) into which it is has been divided are coloured. Therefore, 2/2 = 1; 3/3 = 1; 4/4 = 1. Thus,
From the above figures, we can clearly see that all parts of a whole figure (expressed as 1) into which it is has been divided are coloured. Therefore, 2/2 = 1; 3/3 = 1; 4/4 = 1. Thus,
When the number of coloured parts is the same as the number of equal parts, the fraction is equal to 1.
Now, Try Yourself: Write any four fractions equal to 1.
2. A Fraction Part of a Collection
There are 5 balloons. Three of them are red. We say that 3/5 of the balloons are red and 2/5 of the balloons are green.
Numerator and Denominator
Look at the fraction 2/ 7.
2 is called the numerator.
7 is called the denominator.
The bar drawn in the middle is called a vinculum. The line between the numerator and denominator also has a special name, It is called fraction bar.
The line between the numerator and denominator also has a special name, It is called fraction bar.
Each fraction is written as:
Fractions on the Number Line
Fractions can be represented by points on the number line.
Draw the number line. Mark points for the whole numbers 0 and 1.
- Divide the units into halves. Mark the point of division.
It divides the segment of unit length into two equal parts, so we can name this point as 1/ 2.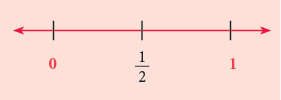
- To represent 1/3 and 2/3 on the number line, divide the segment into 3 equal parts.
The points of division are marked as 1/3 and2/3. (Each part = 1/3)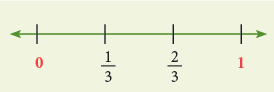
- To represent 1/5, 2/5, 3/5, 4/5 on the number line, divide the unit segment into 5 equal parts.
The points of division are marked as 1/5, 2/5, 3/5and 4/5. (Each part = 1/5)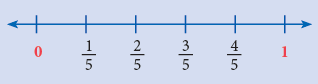
Similarly, we can divide the unit segment into as many equal parts as we like.
Example 1: Represent 4/7 on the number line.
Draw a line. Mark the points A and B for the whole numbers 0 and 1 respectively. Since, the denominator is 7, the total number of equal parts are 7. So, divide the unit segment into 7 equal parts. The numerator 4 shows that 4 parts are to be taken.
Each division = 1/7.
Starting from point A, the fourth point of division P represents the required fraction.
Example 2: Write the fraction represented by point O, on the given number line.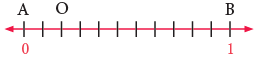
AB has been divided into 11 equal parts. Point O shows that 2 parts are taken. Hence, the fraction that represents the point O = 2/11.
Like and Unlike Fractions
1. Like Fractions
Fractions that have the same denominator are called like fractions.
Examples: 1/5, 2/5, 3/5, 4/5 are like fractions, as they have the same denominator, i.e., 5.
2. Unlike Fractions
Fractions that have different denominators are called unlike fractions.
Examples: 3/4, 7/ 8, 9/7 are called unlike fractions, as they have different denominators.
Equivalent Fractions
Observe the following figures carefully.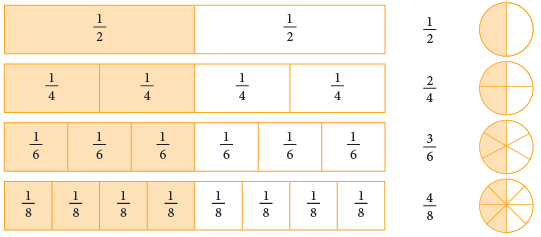 We can see that the coloured portions of these figures are equal. Since the fractions 1/2, 2/4, 3/6, 4/8, all indicate the same part of the rectangle or the circle, we can say that these fractions name the same number. This can be expressed as 1/2 = 2/4 = 3/6 = 4/8 etc.
We can see that the coloured portions of these figures are equal. Since the fractions 1/2, 2/4, 3/6, 4/8, all indicate the same part of the rectangle or the circle, we can say that these fractions name the same number. This can be expressed as 1/2 = 2/4 = 3/6 = 4/8 etc.
They are called equivalent fractions.
Such fractions which represent the same part of an object, though differing in numerals, are called equivalent fractions.
The term equivalent is derived from the words ‘equal’ and ‘value’.
Edurev Tips:The numerator and denominator of a fraction are called terms.
How to Find Equivalent Fractions?
The equivalent fractions given above are all equal to 1/2.
They can also be written as: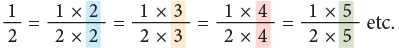 Thus, you can multiply the terms of a fraction by the same number, other than zero to write an equivalent fraction. Multiplying the numerator and denominator of a fraction by the same number does not change the size of the fraction.
Thus, you can multiply the terms of a fraction by the same number, other than zero to write an equivalent fraction. Multiplying the numerator and denominator of a fraction by the same number does not change the size of the fraction.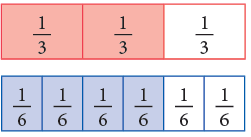 Thus,
Thus,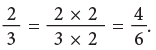
Example 3: Write the next 4 fractions equivalent to 2/5.
that is
Hence, the next four fractions are equivalent to
Example 4: Write the numeral that should replace the question mark to make each sentence true.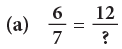
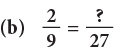
(a)
The numerator 6 has been multiplied by 2 to get 12. So, multiply the denominator also by 2.
(b)
The denominator 9 has been multiplied by 3 to get 27. So, multiply the numerator also by 3.
You can also use division to find equivalent fractions.
Example 5: Write the numeral that should replace the question mark in the following to make the given sentences true.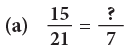
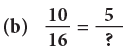
(a)
The denominator 21 has been divided by 3 to get the denominator 7. So, we divide the numerator also by 3.
(b)
The numerator 10 has been divided by 2 to get the numerator 5. So, we divide the denominator also by 2.
Checking whether given Fractions are Equivalent or Not
Consider a pair of equivalent fractions, say, 2/7 = 4/14.
Find the cross-products, as shown.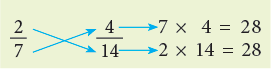
What do you observe about the products?
Ans: They are equal.
This shows that two fractions are equivalent if their cross-products are equal.
Comparing and Ordering Fractions
Aman and Aditi were painting a wall. Aman painted 2/3 of the wall. Aditi painted 1/3 of the wall.
Aman painted 2/3 of the wall. Aditi painted 1/3 of the wall.
Who painted more?
Since, 2/3 > 1/3 or we can say 1/3 < 2/3,
so, Aman painted more.
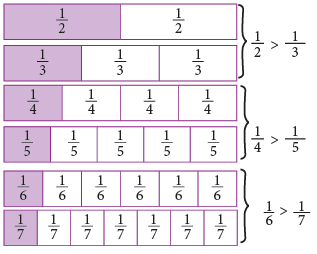
To Compare Like Fractions
Look at the like fractions represented by the figures given below.
To compare like fractions, compare the numerators.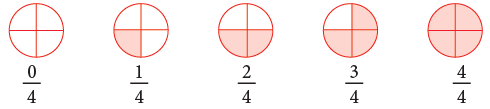 It is clear from the given figures that:
It is clear from the given figures that: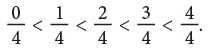
From the above discussion, we arrive at the following rule.
The fraction having the greater numerator is the greater fraction.
Now, observe the following. In the first row, 4 hats out of 9 hats are coloured. Thus, fraction of coloured hats is 4/9.
In the first row, 4 hats out of 9 hats are coloured. Thus, fraction of coloured hats is 4/9.
In the second row, 7 hats out of 9 hats are coloured. Thus, fraction of coloured hats is 7/9.
Since, the second group has more number of coloured hats, so,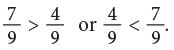
To Compare Fractions with the Same Numerator
The following figures represent fractions with the same numerator.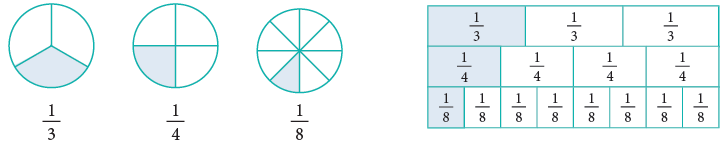 It is clear from the above figures that,
It is clear from the above figures that,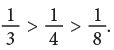
Let us study more examples.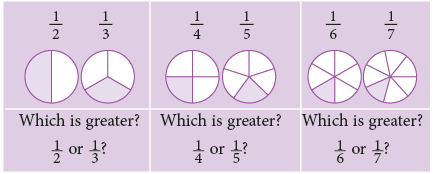
 From the above discussion, we arrive at the following rule:
From the above discussion, we arrive at the following rule:
Rule: In fractions which have the same numerator, the fraction having a smaller denominator names a greater fraction than the fraction having a larger denominator.
Example 6: Fill in the  with < or >.
with < or >.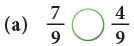
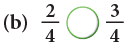
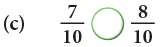
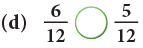
Edurev Tips: Like fractions with greater numerator are greater.
Example 7: Arrange the following fractions in ascending order.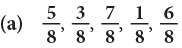
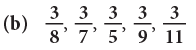
(a) Since, 1 < 3 < 5 < 6 < 7.
The fraction with the smaller numerator names the smaller fraction.
Here, the fractions in ascending order are
(b)The fraction with the greater denominator names the smaller fraction.
Here, the fractions in ascending order are
Example 8: Arrange the following fractions in descending order.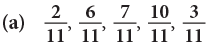
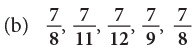
(a) The given fractions have the same denominator. So, they are like fractions.
The fraction with the greater numerator names the greater fraction.
Thus, the fractions in descending order are:
(b)The given fractions have the same numerator.
The fraction with the smaller denominator names the greater fraction.
Thus, the fractions in descending order are:
Reducing a Fraction to its Lowest Form
You have seen that 1/2, 2/4, 3/6, 4/8 are all fractions equal to the fraction for one-half. The lowest fraction is 1/ 2. This is called the lowest form because there is no number except 1, that will divide exactly into both the numerator and denominator of this fraction. The fractions 1/ 3, 3/4, 5/8, 7/16 are all in their lowest form.
Study the following examples:
Example 9: Express 20/32 in the lowest form.
Edurev Tips: You can divide 20 and 32 by common factors. Start with 2.
Example 10: Express each of the following fractions in the lowest form.
(a) 9/15
(b) 52/72
(c) 55/80
(a)
(b)
(c)
Edurev Tips: We start by trying to divide both the numerator and the denominator by common factors, from the lowest to the highest, till the only common factor is 1.
Kinds of Fractions
1. Unit Fractions
The fractions which have 1 as the numerator are called unit fractions.
Examples: 1/5, 1/20, 1/87 etc., are all unit fractions.
2. Proper and Improper Fractions
A fraction in which the numerator is less than the denominator is called a proper fraction.
Examples: 2/5, 3/7, 7/10 are all proper fractions.
The picture given alongside shows a pizza divided into 4 equal parts.
4/4 or four quarters is a whole or 1.
What do we get if we add a quarter more to 4/4?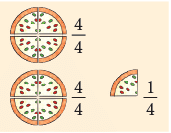 4/4 and 1/4 = 5/4 . 5/4 is a whole and a quarter or 1 + 1/ 4.
4/4 and 1/4 = 5/4 . 5/4 is a whole and a quarter or 1 + 1/ 4.
Fractions such as 5 4 in which the numerator is greater than the denominator are called improper fractions.
(i) Mixed Numbers
A mixed number is a mixture of a whole number and a proper fraction.
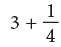 is an expanded numeral.
is an expanded numeral.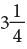 is a compact numeral.
is a compact numeral. 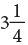 is called a mixed numeral or a mixed number, since part of the numeral is a whole number, 3 and part is a fractional numeral, 1/4.
is called a mixed numeral or a mixed number, since part of the numeral is a whole number, 3 and part is a fractional numeral, 1/4.
Observe the following: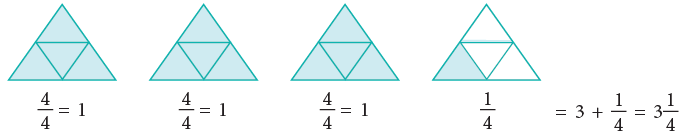
(a) Converting an Improper Fraction into Mixed Number
Suppose Vibha’s mother wants to distribute 17 mangoes among 5 children.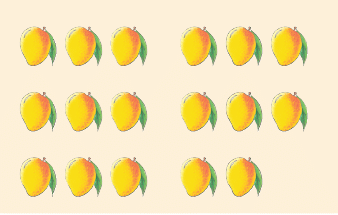 17 ÷ 5 = 3 and 2 remains.
17 ÷ 5 = 3 and 2 remains.
We may also write 17 ÷ 5 as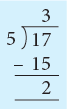
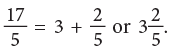
17 ÷ 5 = 3 R 2.
Rule: An improper fraction can be changed into a mixed number by dividing the numerator by the denominator. The quotient gives the whole number part of the mixed number, while the remainder placed over the denominator gives the fractional part.
Example 11: Convert each of the following fractions to a mixed numeral.
(a) 37 / 6
(b) 93 / 27
(a)On dividing 37 by 6, we get 6 as quotient and 1 as remainder.
Therefore,
(b)Dividing 93 by 27, we get quotient = 3, remainder = 12
Therefore,
(b) Converting Mixed Numbers into Improper Fractions
Rule: A mixed number is changed into an improper fraction by multiplying the whole number by the denominator of the fraction and adding to the product the numerator of the fraction. The result so obtained forms the new numerator of the improper fraction.
Example 12: Convert 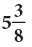 into an improper fraction.
into an improper fraction.
Multiply 5 by 8 and add 3 to the product.
(c) Using Division to Find Fractional Part of a Whole Number
Priya had 8 oranges. She gave half of them to her sister Teena. How many did each of them get?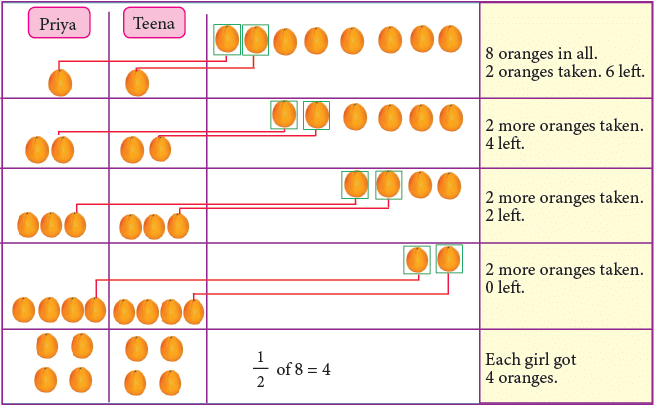 You know that you have to find 1/ 2 of 8. This, as you have seen in the picture, is equal to 4.
You know that you have to find 1/ 2 of 8. This, as you have seen in the picture, is equal to 4.
The drawing shows that a group of 2 oranges was taken, each time both girls chose an orange.
Taking groups of 2 from 8, until none is left, is the same as dividing 8 by 2, that is,
8 – 2 – 2 – 2 – 2 = 0 is the same as 8 ÷ 2 = 4.
Therefore, we conclude that,
1/2 of 8 = 8 ÷ 2 = 4.
Now, you can also find 2/3 of 6, as shown below.
2/3 of 6 = 2 × (6 ÷ 3) = 2 × 2 = 4;
2/ 3 of 6 = (2 × 6) ÷ 3 = 12 ÷ 3 = 4.
Edurev Tips:
- 1/3 of 6 as 6 ÷ 3 and write directly 1/3 of 6 = 2.
- 3/4 of 16 as 3 × (16 ÷ 4) or (3 × 16) ÷ 4 by working out mentally 16 ÷ 4 = 4 and 3 × 4 = 12.
Examples:
- 7/ 8 of 24 m = 7/8 × 24 m = [7 × (24 ÷ 8)]m = (7 × 3)m = 21 m
- 4/5 of ₹ 50 = ₹ (4/5 × 50) = ₹ 4 × (50 ÷ 5)] = ₹ (4 × 10) = ₹ 40
- 5/12 of 1 hour = 5/12 of 60 minutes = 5 × (60 ÷ 12) minutes = (5 × 5) minutes = 25 min.
Addition of Like Fractions
Mamta’s mother has a bar of chocolate. She divided it into 8 pieces and gave one piece to Mamta and two pieces to her brother Mayank.
What fraction of the whole chocolate did she distribute between them?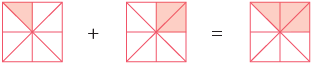 Mamta’s share + Mayank’s share
Mamta’s share + Mayank’s share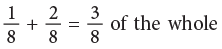
Look at the other examples: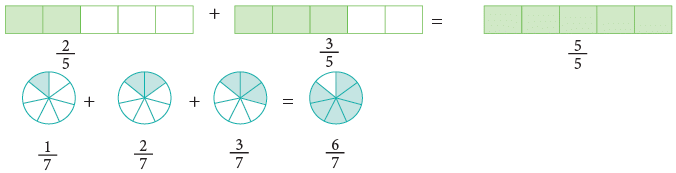
Edurev Tips: When you add like fractions
- Add the numerators.
- Write the sum over the same denominator.
Addition of Like Fractions on Number Line
You can also use a number line to show the addition of fractions. The following number line shows the sum of 2 / 7 and 3 / 7. The above example shows that:
The above example shows that: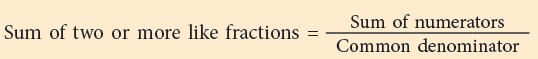
Subtraction of Like Fractions
Madhavi had four-fifths of a cake. She gave one-fifth of it to Ashu. How much cake is left with her?
Clearly, this is a problem of subtraction. So, cake left with her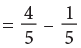
This can be illustrated by a diagram as shown:
Total coloured parts = 4.
Number of coloured parts removed = 1
Remaining coloured parts = 3.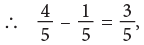
which can also be written as: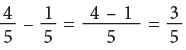
Subtraction can also be shown on a number line as under: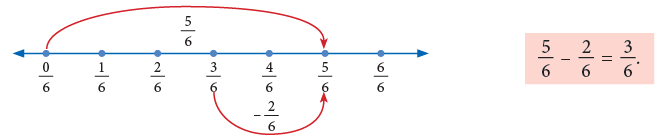 Thus,
Thus,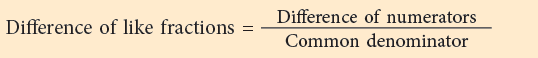
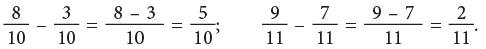
|
33 videos|168 docs|30 tests
|
FAQs on Fractions Class 4 Notes Maths
| 1. What is a fraction and how is it represented? |  |
| 2. How can I identify equivalent fractions? |  |
| 3. How do I compare and order fractions with different denominators? |  |
| 4. What does it mean to reduce a fraction to its lowest form? |  |
| 5. How do I add or subtract like fractions? |  |