Class 6 Exam > Class 6 Notes > Chapter Notes: Fundamental Concepts of Algebra
Fundamental Concepts of Algebra Chapter Notes - Class 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Constants and Variables |

|
| Matchstick Patterns |

|
| Use of Variables |

|
| Terms |

|
| Coefficient |

|
| Algebraic Expressions |

|
Introduction
Algebra is like a magical language in mathematics that helps us solve puzzles and find patterns using numbers, letters, and symbols. Imagine you're a detective trying to figure out how many candies you need for your friends or how many matchsticks make a cool pattern! Algebra uses tools like letters (a, b, x, y) and symbols (+, −, ×, ÷) to create general rules for such problems. The word "algebra" comes from an ancient book called 'Aljebar w'al almugabalah,' which means solving equations. In this chapter, we'll explore how algebra helps us describe patterns, calculate quantities, and express relationships in a fun and simple way!

Constants and Variables
- A constant is a number with a fixed value that never changes.
- Examples of constants include 2, -5, 10, and 3/7.
- A variable is a letter or symbol whose value can change.
- Examples of variables include x, y, z, 6a, and 7b.
- Variables are also called literal numbers or literals.
- A combination of constants and variables (like 3x or 5ab) is treated as a variable because its value depends on the variable.
- All rules of addition, subtraction, multiplication, and division for numbers apply to literals too.
Example: In the expression 4n, where n is the number of students, 4 is a constant, and n is a variable. If n = 2, then 4n = 4 × 2 = 8 toffees are needed.
Matchstick Patterns

- Matchstick patterns help us find general rules for the number of matchsticks needed to form shapes like squares or triangles.
- We observe the pattern, create a table, and use a variable to write a formula.
- Formula for squares: Number of matchsticks = 3n + 1, where n is the number of squares.
- Formula for triangles: Number of matchsticks = 3n, where n is the number of triangles.
Example: For a pattern of letter 'S', the number of matchsticks needed is 5n, where n is the number of 'S' letters. For 3 letters, 5 × 3 = 15 matchsticks are required.

Use of Variables
- Variables are used to write general formulas for real-life situations or geometric properties.
- They help express quantities that depend on other factors, like the number of items or measurements.
Example: If a box contains 60 apples, the total number of apples for n boxes is 60n. For 5 boxes, 60 × 5 = 300 apples.
Perimeter of a Square
- The perimeter of a square is the total length of its four sides.
- Formula: Perimeter = 4 × side length = 4l, where l is the side length.

Example: For a square with side length l = 5 cm, the perimeter is 4 × 5 = 20 cm.
Area of a Rectangle
- The area of a rectangle is the product of its length and breadth.
- Formula: Area = length × breadth = l × b, where l is length and b is breadth.
- Here, l and b are variables that can take any positive value.
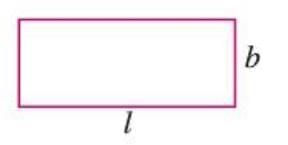
Example: For a rectangle with length l = 6 cm and breadth b = 4 cm, the area is 6 × 4 = 24 cm2.
Total Length of Edges of a Cube
- A cube has 12 edges, all of equal length.
- Formula: Total length of edges = 12 × edge length = 12l, where l is the edge length.
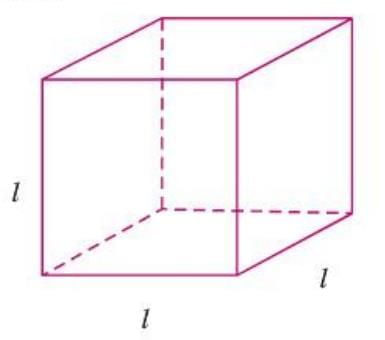
Example: For a cube with edge length l = 3 cm, the total length of edges is 12 × 3 = 36 cm.
Terms
- A term is a single constant, variable, or a product/quotient of constants and variables.
- Examples: 5, 15ab, 7/y are terms.
- A constant term has no variable, e.g., 5 or -3.
- In a term, the constant part is the numerical factor, and the variable part is the literal factor.
- Example: In -4xy, -4 is the numerical factor, and x, y, xy are literal factors.
Example: In the term 5ab, 5 is the numerical factor, and ab is the literal factor.
Like Terms
- Like terms have the same literal factors with the same powers.
- They differ only in their numerical factors.
- Example: 6xy and -7xy are like terms because they both have xy.
Example: 17a2b and 1/5a2b are like terms.
Unlike Terms
- Unlike terms have different literal factors or different powers.
- Example: 3x2 and 3xy are unlike terms because their literal factors differ.
Example: 4a2b and ab are unlike terms.
Coefficient
- A coefficient is any factor of a term when considered as a product of the remaining factors.
- In x2y, the coefficient of x2 is y, and the coefficient of y is x2.
Example: In 2/3xy, the coefficient of xy is 2/3.
Algebraic Expressions
- An algebraic expression is a combination of one or more terms joined by + or −.
- Examples:
- ab (1 term),
- 3xy + x/a (2 terms),
- 2x2 + y2 − x/y (3 terms).
- Expressions can have variables with negative or fractional powers, but these are not polynomials.
Example: The expression 2a2 − a3 + 5ab + 10 has four terms: 2a2, -a3, 5ab, and 10.
Monomial
- A monomial is an algebraic expression with exactly one non-zero term and whole number powers of variables.
- Examples: a, xy, 5xy, 3/7ab.
Example: 100x is a monomial with one term.
Binomial
- A binomial is an algebraic expression with exactly two non-zero terms and whole number powers of variables.
- Examples: 3x + a, 5x + 17y, a + b.
Example: −7xy + x2 is a binomial with two terms.
Trinomial
- A trinomial is an algebraic expression with exactly three non-zero terms and whole number powers of variables.
- Examples: x + y2 + 5a, xy + z + 2ab.
Example: 12y + 6x − 7 is a trinomial with three terms.
Polynomial
- A polynomial is an algebraic expression with a finite number of non-zero terms and whole number powers of variables.
- All monomials, binomials, and trinomials with whole number powers are polynomials.
- Expressions with negative or fractional powers (like √x or 1/m) are not polynomials.
Example: 1 + 2a + 21a3 is a polynomial with degree 3.
Degree of a Polynomial
- The degree of a polynomial is the highest power of the variable in any of its terms.
- A constant polynomial (like 7) has degree 0.
Example: For x + 3x2 − 9x3, the degree is 3 (highest power of x).
Solved Examples
Example 1: Find the rule for the number of matchsticks needed for a pattern of letter 'A'.
Solution: For n letters 'A', the number of matchsticks is 4n + 2. For 5 letters, 4 × 5 + 2 = 22 matchsticks.

Example 2: Sita is 7 years younger than Radha. Express Radha's age in terms of Sita's age.
Solution: Let Sita's age be x years. Radha's age = x + 7 years.
Example 3: Separate the following into pairs of like terms: 2xy, −4a, x2y, 1/3ab, a, 5ab, 6x2y, −14/15xy.
Solution: Pairs are: (2xy, −14/15xy), (−4a, a), (x2y, 6x2y), (1/3ab, 5ab).
Example 4: Find the coefficient of xy in −a2bxy.
Solution: The factors other than xy are −a2 and b. Thus, the coefficient is −a2b.
Example 5: Classify −7xy + x2 as monomial, binomial, or trinomial.
Solution: It has two terms (−7xy, x2), so it is a binomial.
Solution: For n letters 'A', the number of matchsticks is 4n + 2. For 5 letters, 4 × 5 + 2 = 22 matchsticks.

Example 2: Sita is 7 years younger than Radha. Express Radha's age in terms of Sita's age.
Solution: Let Sita's age be x years. Radha's age = x + 7 years.
Example 3: Separate the following into pairs of like terms: 2xy, −4a, x2y, 1/3ab, a, 5ab, 6x2y, −14/15xy.
Solution: Pairs are: (2xy, −14/15xy), (−4a, a), (x2y, 6x2y), (1/3ab, 5ab).
Example 4: Find the coefficient of xy in −a2bxy.
Solution: The factors other than xy are −a2 and b. Thus, the coefficient is −a2b.
Example 5: Classify −7xy + x2 as monomial, binomial, or trinomial.
Solution: It has two terms (−7xy, x2), so it is a binomial.
FAQs on Fundamental Concepts of Algebra Chapter Notes - Class 6
| 1. What are constants and variables in algebra? |  |
Ans. In algebra, constants are fixed values that do not change, such as numbers like 5 or -3. Variables, on the other hand, are symbols (commonly letters like x, y, or z) that represent unknown values or quantities that can change. For example, in the expression 2x + 3, '2' is a coefficient (a constant), 'x' is a variable, and '3' is another constant.
| 2. How can matchstick patterns illustrate algebraic concepts? |  |
Ans. Matchstick patterns are a visual way to understand algebraic concepts by representing numbers and relationships through physical arrangements. For example, if a pattern adds one matchstick for each new figure in a series, students can create an expression to represent the number of matchsticks needed for any figure in the pattern. If the first figure uses 3 matchsticks and each subsequent figure adds 2, the nth figure can be expressed as 2n + 1.
| 3. What is the significance of coefficients in algebraic expressions? |  |
Ans. Coefficients are the numerical factors in algebraic expressions that multiply the variables. For example, in the expression 4x + 2y, '4' is the coefficient of 'x' and '2' is the coefficient of 'y'. They indicate how many times the variable is being counted, making them essential for understanding the magnitude of each term in an expression.
| 4. What are algebraic expressions, and how are they formed? |  |
Ans. Algebraic expressions are combinations of variables, constants, and coefficients, connected by mathematical operations such as addition, subtraction, multiplication, or division. They can represent real-world situations and can be formed by using variables to generalize numerical relationships. For example, the expression 5a + 3b represents a situation where 'a' and 'b' can take on various values.
| 5. Why is understanding terms in algebra important? |  |
Ans. Understanding terms in algebra is crucial because they are the building blocks of algebraic expressions. Each term consists of a coefficient and a variable (or just a constant). Knowing how to identify and manipulate terms helps in simplifying expressions, solving equations, and understanding how different parts of an expression relate to one another.
Related Searches














