Implicit Differentiation Chapter Notes | Calculus AB - Grade 9 PDF Download
Welcome back to our AP Calculus journey with Fiveable! Today, we’re diving into implicit differentiation, a powerful technique for finding derivatives when variables can’t be easily isolated. Building on our previous lesson about the chain rule, let’s explore how to handle equations where y isn’t explicitly solved for.
Understanding Implicit Differentiation
In calculus, we often deal with explicit equations like y = x², where y is directly expressed in terms of x. However, some equations, like xy² = xy + 1, are implicit, meaning y isn’t isolated. Implicit differentiation helps us find the derivative dy/dx for such equations.
The process involves differentiating both sides of the equation with respect to x, applying the chain rule for terms involving both x and y, and then solving for dy/dx. Unlike explicit differentiation, we use dy/dx or y' notation instead of f'(x).
Steps for Implicit Differentiation
Here’s a clear guide to differentiate implicitly:
- Indicate that you’re differentiating with respect to x.
- Differentiate both sides of the equation, using derivative rules like the power rule and chain rule.
- Solve for dy/dx by isolating it, often by factoring it out.
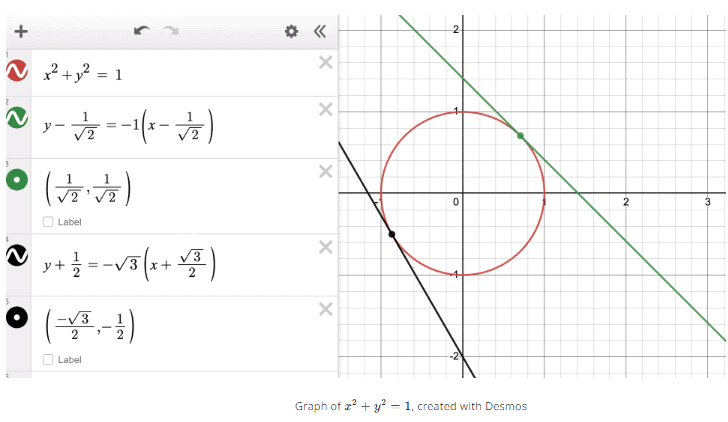
Example: Implicit Differentiation with the Unit Circle
Implicit Differentiation is best learned through practice, so let's go through and find dy/dx for the unit circle, x2 + y2 = 1.
First, we need to notate that we are differentiating.
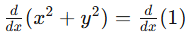
Next, we can apply our knowledge of the Power Rule and the Chain Rule.
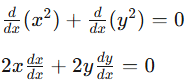
Because dx/dx = 1, we can leave it off when doing the chain rule for this equation.
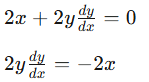
Lastly, isolate dy/dx and you get the final answer of…
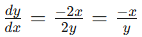
We can see this holds true in the graph below! The slope of the graph at any point can be represented by dy/dx = (-x)/y .
For example, at the point
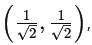 we can calculate…
we can calculate…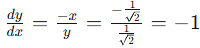
At the point
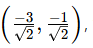 we can calculate…
we can calculate…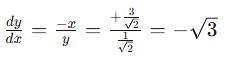
Practice Problem: Implicit Differentiation and Tangent Lines
Let’s tackle a free-response question inspired by the 2015 AP Calculus AB exam (credit to College Board).
Consider the curve defined by y³ - xy = 2.
(a) Find dy/dx.
1. Differentiate both sides with respect to x:
d/dx (y³ - xy) = d/dx (2)
d/dx (y³) - d/dx (xy) = 0
2. Apply the chain rule and product rule:
3y² * dy/dx - (x * dy/dx + y) = 0
3. Simplify and isolate dy/dx:
3y² * dy/dx - x * dy/dx - y = 0
dy/dx (3y² - x) = y
dy/dx = y / (3y² - x)
(b) Find the equation of the tangent line at (-1, 1).
Use the point-slope form: y - y₁ = m (x - x₁), where x₁ = -1, y₁ = 1, and m = dy/dx at (-1, 1).
Calculate the slope:
dy/dx = y / (3y² - x) = 1 / (3(1)² - (-1)) = 1 / (3 + 1) = 1/4
Now, write the tangent line equation:
y - 1 = (1/4)(x - (-1))
y - 1 = (1/4)(x + 1)
This equation, y - 1 = (1/4)(x + 1), is the tangent line at (-1, 1). Great work—this would score full points on the AP exam!
|
26 videos|75 docs|38 tests
|
FAQs on Implicit Differentiation Chapter Notes - Calculus AB - Grade 9
| 1. What is implicit differentiation and why is it used? |  |
| 2. How do you perform implicit differentiation step by step? |  |
| 3. Can you provide an example of implicit differentiation using the unit circle equation? |  |
| 4. How can implicit differentiation help in finding tangent lines to curves? |  |
| 5. What are common mistakes to avoid when using implicit differentiation? |  |















