Integers Class 7 Notes Maths Chapter 1
What are Negative Numbers?
Ethan is going for a picnic with his friends. He wants to carry cupcakes with him, but he has got only 3 cupcakes and there are 4 friends. What is he going to do now?

So, Ethan decided to borrow one cupcake from his sister, which he would return later.
How many cupcakes does he have now?
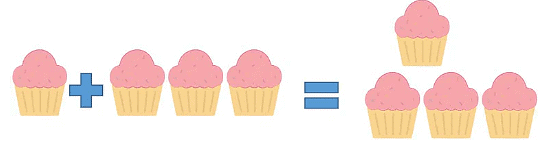
After borrowing one cupcake from his sister, he has got 4 cupcakes, which he would give to his four friends.
He goes for the picnic, where he gave away the 4 cupcakes to his friends.
Now, how many cupcakes are left with him?
Is your answer zero (0)?
We can say that there are no or 0 cupcakes left with him, but we also have to keep in mind that he has borrowed one cupcake from his sister.
So, in actual Ethan has (-1) cupcake, which means that 1 cupcake is borrowed and did not belong to him.
If he buys 3 more cupcakes the next day, he will have to return 1 cupcake to his sister and will be left with 2 cupcakes only.
Numbers with a negative sign are less than zero, and they are called negative numbers.

 Positive and Negative Numbers
Positive and Negative Numbers
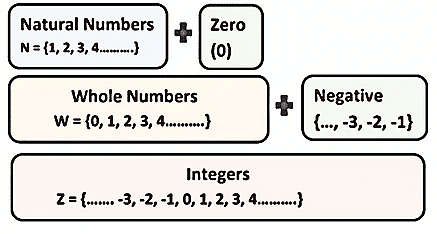
Natural Numbers: Natural Numbers is a set of counting numbers. They are denoted by N.

Whole Numbers: If zero is included in the collection of natural numbers, we get a new collection of numbers known as whole numbers.

Integers: Integers are a set of whole numbers and negative of all natural numbers.
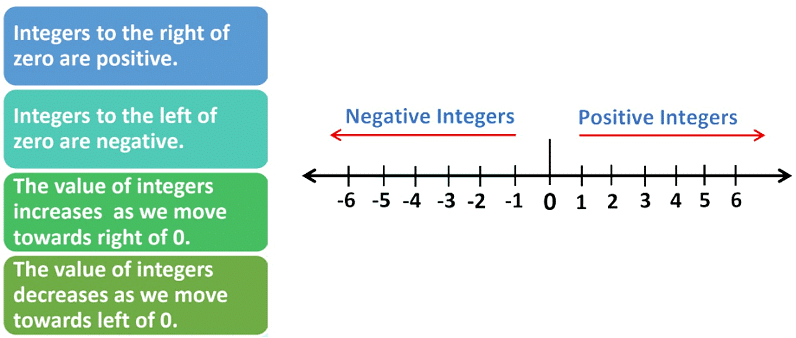
Integers on a Number Line
Addition of Integers

If we add 6 and 4 (both are positive integers), we add their values and the result will also be a positive integer.
So, 6 + 4 = 10
Example 1: Add 25 and 46
25 and 46 are positive integers. So, we add their values.
25 + 46 = 71The result will be a positive integer. (a common sign of both the integers)

Example 2: Add 6 + (-9)
Here, one integer is positive and the other integer is negative.
So, we find the difference of the integers, (9 – 6 = 3)
Out of the two integers, which one is greater (do not consider the sign of the integers here)?
9 is the greater integer, but it is a negative integer.
Therefore, result 3 will have a negative sign.
So, -9 + 6 = -3
Example 3: Add -67 and 32
-67 + 32
Here, one integer is positive and the other is negative so we find the difference of their numerical values.
67 – 32 = 35
Now, 67 is the greater integer (signs of the integers are not considered).
As 67 is a negative integer, the result will take the negative sign.
-67 + 32 = -35

Example 4: Add: -5 and -3
-5 + (-3) = -5 – 3 = -8
If we do the addition of -5 and -3 on the number line, then we start from 0 and jump 5 places to the left of 0.
Now, we again jump 3 places to the left of -5. Therefore, we reach -8.
Example 5: Add -78 and -36
Both the integers are negative, so we add their values and the result will take the negative sign.
-78 + (-36) = -78 – 36 = -114
Subtraction of Integers
When we subtract one integer from another, we add the additive inverse of the integer being subtracted. Example 6: Subtract 3 from 7.
Example 6: Subtract 3 from 7.7 – 3
Additive inverse of 3 is -3
So we add 7 to the additive inverse of 3 that is -3.
7 -3 = 7 + (-3) = 4
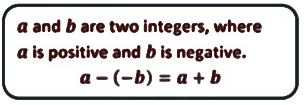
Example 7: Subtract -26 from 48
Here, we are subtracting the negative integer, -26 from 48. So we simply add the two integers.
48 – (-26)
48 – (-26) = 48 + 26 = 74
Example 8: Subtract -89 from -67
Now, we have to subtract a negative integer, -89 from another negative integer, -67.
-67 – (-89) = -67 + 89
We know that when we add a positive and a negative integer, then we find their difference and put the sign of the greater integer.
-67 + 89 = 22 (sign will be positive as the greater integer, 89 has a positive sign)
Properties of Addition and Subtraction of Integers
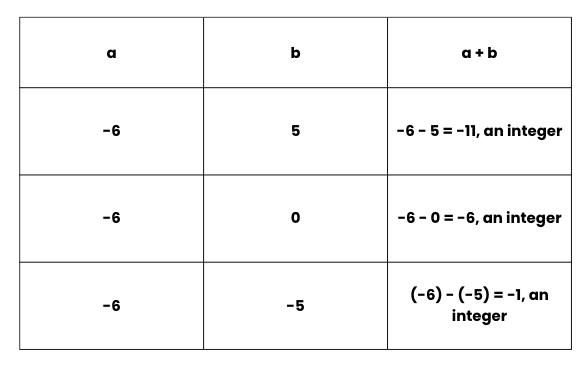
1. Closure under Addition
If a and b are two integers, then a + b is also an integer.
When we add any two integers, the result will always be an integer.
This is true for all integers.
2. Closure under Subtraction
If a and b are two integers, then a − b is also an integer.
When we subtract an integer from another, the result will always be an integer. This is true for all integers.
3. Commutative Property
Commutative property of addition of integers
If a and b are two integers, then a + b = b + a
Hence, we can add two integers in any order.

Commutative property of subtraction of integers
If a and b are two integers, then a − b ≠ b − a


Example 9: Verify the following and state the property used.
(-5) + (-8) = (-8) + (-5)
LHS
-5 + (-8) = -5 – 8 = -13
RHS
-8 + (-5) = -8 – 5 = -13
LHS = RHS
Here, we have used the commutative property of addition of integers which states that, if a and b are two integers, then a + b = b + a
4. Associative Property
Associative property of Addition of IntegersIf a, b & c are any three integers, then
(a + b) + c = a + (b + c)

When we are adding integers, they can be grouped in any order and the result remains the same.
Consider the three integers, -2, -4 and -6
Case 1: [-2 + (-4)] + (-6)
In the first case, we group -2 and -4.
[-2 + (-4)] + (-6) = -6 + (-6)
On a number line, we start from -6 and jump 6 places to the left of -6.
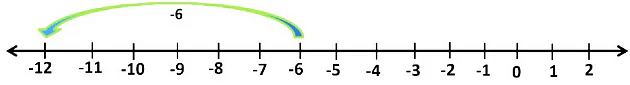
We reach -12 on the number line.
Case 2: (-2) + [-4 + (-6)]
In the second case we group together -4 and -6.
(-2) + [-4 + (-6)] = -2 + (-10)
On a number line, we start from -2 and jump 10 places to the left of -2.

We reach -12 on the number line.
We see that the result is the same in both cases.

Associative property of Subtraction of Integers
For any three integers a, b and c,
(a – b) – c ≠ a – (b – c)

Consider the integers, -3, -5 and -6
Case 1: [-3 - (-5)] - (-6)
In the first case, we group -3 and -5.
[-3 - (-5)] - (-6) = 2 + 6 = 8
Case 2: (-3) – [-5 – (-6)]
In the second case, we group -5 and -6.
(-3) – [-5 – (-6)] = -3 – 1 = -4
[-3 - (-5)] - (-6) ≠ (-3) – [-5 – (-6)]

Example 10: Fill in the blanks to make the following statements true.
(i) [13 + (-12)] + (___) = 13 + [(-12) + (-7)]
We have used the associative property of addition of integers which states that, if a, b & c are any three integers, then
(a + b) + c = a + (b + c)
If a = 13, b = -12 and c = -7 then,
[13 + (-12)] + (-7) = 13 + [(-12) + (-7)]
(ii) (-4) + [15 + (-3)] = [-4 + 15] + (__)
We use the associative property of addition of integers which states that, if a, b & c are any three integers, then
(a + b) + c = a + (b + c)
If a = -4, b = 15 and c = -3 then,
(-4) + [15 + (-3)] = [-4 + 15] + (-3)
5. Additive Identity
If a is any integer, then a + 0 = a = 0 + a
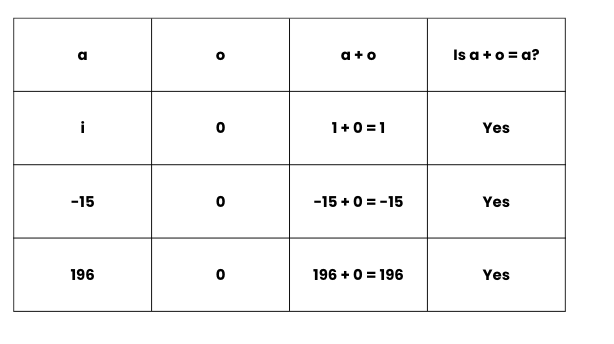
The number 'zero' has a special role in addition. When we add zero to any integer, the result is the same integer again. Zero is the additive identity for integers.
Example 11: Fill in the blanks
(i) (-23) + 0 = ____
If we add zero to any integer the result is the same integer again. This property is known as additive identity property.
So, (-23) + 0 = -23
(ii) 0 + ___ = -43
We again use the additive identity property.
So, 0 + (-43) = -43
(iii) 8 + ___ = 8
Using the additive identity property, we get, 8 + 0 = 8
Multiplication of Integers
Multiplication of a Positive and a Negative Integer
To find the product of two integers with unlike signs, we find the product of their values and put the negative sign before the product.
For any two integers a and b,
a × (−b) = (−a) × b = −(a × b)
Example 12: Find
(i) (-31) × 30
The two integers have different signs, one is positive and the other is negative. So we find the product of their values and give the product a negative sign.
(-31) × 30 = -930
(ii) 26 × (-13)
Here, one integer is positive and the other integer is negative. So, we find the product of their values and put a negative sign before the product.
26 × (-13) = -338
Multiplication of Two Negative Integers
To find the product of two integers with the same sign, we find the product of their values and put the positive sign before the product.
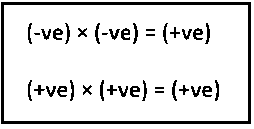
For any two positive integers a and b,
a × b = ab
For any two negative integers (−a) and (−b)
(−a) × (−b) = ab
Consider two positive integers, 6 and 8
6 × 8 = +48
Now, consider the two negative integers -6 and -8
(-6) × (-8) = +48
We see that the product is positive in both cases.
Example 13: Find
(i) (-11) × (-100)
The two integers have the same sign (negative), so we find the product of their values and put the positive sign before the product.
(-11) × (-100) = +1100
(ii) 25 × 250
As the two integers are positive (same sign) we find the product of their values and give a positive sign to the product.
25 × 250 = 6250
Product of three or more Negative Integers
We know that the product of two negative integers is a positive integer. What happens if we have to find the product of more than two negative integers?

We see that when the number of negative integers in a product is even, then the product is an even integer and if the number of negative integers in the product is odd, then the product is a negative integer.
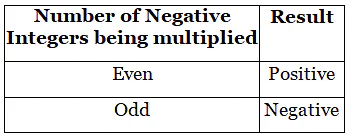
Properties of Multiplication of Integers
1. Closure under Multiplication
If a and b are two integers, then a × b is an integer.

2. Commutativity of Multiplication
If a and b are two integers, then a × b = b × a

The value of the product does not change even when the order of multiplication is changed.
3. Multiplication by Zero (0)
If a is any integer, then a × 0 = 0 × a = 0
15 × 0 = 0
(-100)× 0 = 0
0 ×(-25) = 0
The product of a negative integer and zero is always zero.
4. Multiplicative Identity
If a is any integer, then a × 1 = a = 1 × a
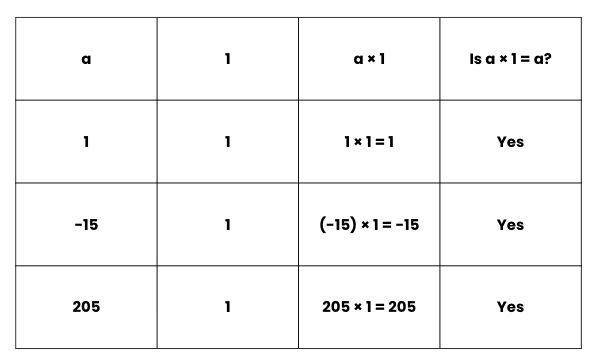
If we multiply any integer by 1, the product is the integer itself.
So, 1 is the multiplicative identity of integers.
Distributive Property of Multiplication over Addition:
If a, b & c are any three integers, then
a × (b + c) = a × b + a × c
5. Associativity for Multiplication
If a, b & c are any three integers, then
(a × b) × c = a × (b × c)
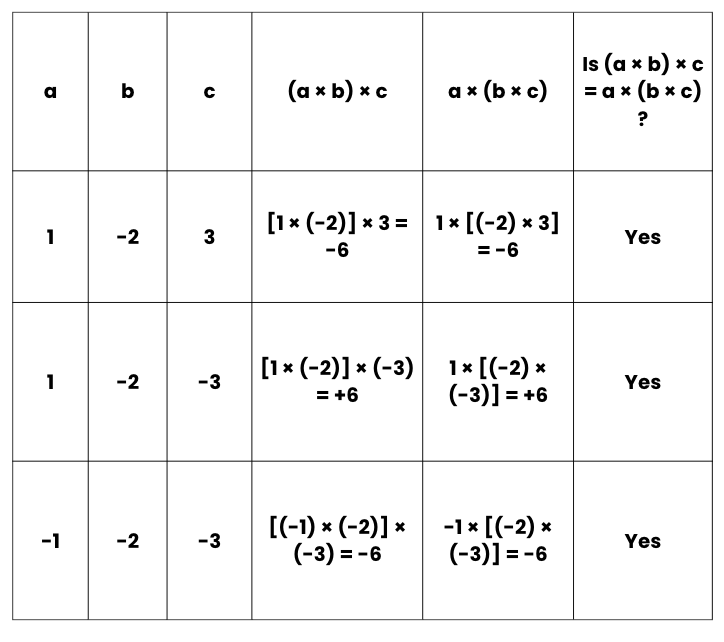
When we multiply three or more integers, the value of the product remains the same even if they are grouped in any manner and this is called the associative property for multiplication of integers.
6. Distributive Property
Over addition: For any integers a, b and c,
a x (b+c) = a x b + a x c
Over Subtraction: For any integers a, b and c,
a x (b-c) = a x b - a x c
Example 14: Find the product using suitable property.
(i) 26× (-48) + (-48)× (-36)
= (-48)×26 + (-48)×(-36)
(by commutative property,a × b = b × a)
= (-48)×[26 + (-36)]
= (-48)×[26 – 36]
= (-48)×(-10) = 480
(ii) 8×53×(-125)
= 53×[8×(-125)]
(by associative property of multiplication (a × b) × c = a × (b × c))
= 53×(-1000) = -53000
(iii) (-41)×101
= (-41)×(100 + 1)
= (-41)×100 + (-41)× 1
(By the Distributive Property of Multiplication over Addition,a × (b + c) = a × b + a × c)
= -4100 + (-41)
= -4100 – 41 = -4141
Example 15: A certain freezing process requires that room temperature be lowered from 50°C at the rate of 6°C every hour. What will be the room temperature 12 hours after the process begins?
Initial room temperature = 50°C
Decrease in temperature in 1 hour = -6°C
Decrease in temperature in 12 hours = 12 × (-6) = - 72°C
Final temperature = 50°C + (- 72°C) = -22°C
Division of Integers
Rule 1: If two integers of different signs are divided, then we divide them as whole numbers and give a negative sign to the quotient.
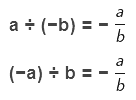
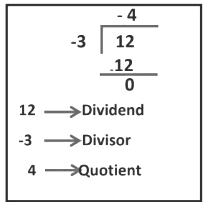
Consider the two integers, 12 and -3.
If we divide 12 by -3, we get,
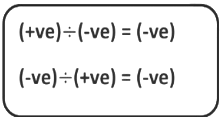
Example 16: Evaluate each of the following:
(i) (−30) ÷ 10
(−a) ÷ b = − (a/b)
(−30) ÷ (10) = − (30/10) = -3
(ii) 49 ÷ (−49)
a÷ (-b) = − (a/b)
49 ÷ (−49) = − (49/49) = -1
(iii) 13 ÷ [(−2) + 1]
= 13 ÷ (−1)
a ÷ (−b) = − (a/b)
= 13 ÷ (−1) = − (13/1)= - 13
Rule 2: If two integers of the same signs are divided, then we divide them as whole numbers and give a positive sign to the quotient.
(−a) ÷ (−b) = a/b
a ÷ b = a/b
On dividing 25 by 5 we get,
25 ÷ 5 = 25/5 = 5
If we divide (-25) by (-5) we get,
(−25) ÷ (−5) = (-25/-5) = 5
We see that the result is the same in both cases.
Example 17: Evaluate each of the following:
(i) (−36) ÷ (−4)
(−a) ÷ (−b) = a/b
= (−36) ÷ (−4) = 36/4 = 9
(ii) (−31) ÷ [(−30) + (−1)]
= (−31) ÷ [(−30) + (−1)]
= (−31) ÷ (−31)
(−a) ÷ (−b) = a/b
(−31) ÷ (−31) = 31/31 = 1
(iii) [(−6) + 5] ÷ [(−3) + 2]
= (−1) ÷ (−1)
(−a) ÷ (−b) = a/b
(−1) ÷ (−1) = 1/1 = 1
Example 18: Write five pairs of integers (a, b) such that a ÷ b = – 4.
Five pairs of integers are,
(i) (8, −2)
a ÷ (−b) = − (a/b)
8 ÷ (−2) = − (8/2) = -4
(ii) (−4 , 1)
(−a) ÷ b = - (a/b)
= (−4 ) ÷ 1 = − 4/1 = -4
(iii) (−16, 4)
(−a) ÷ b = − (a/b)
(−16) ÷ 4 = - 16/4) = -4
(iv) (−24, 6)
(−a) ÷ b = − (a/b)
(−24) ÷ 6 = − (24/6) = -4
(v) (36, −9)
a ÷ (−b) = - (a/b)
36 ÷ (−9) = − (36/9) = -4
Properties of Division of Integers
1. Closure Property
If a and b are two integers, then a ÷ b is not always an integer.


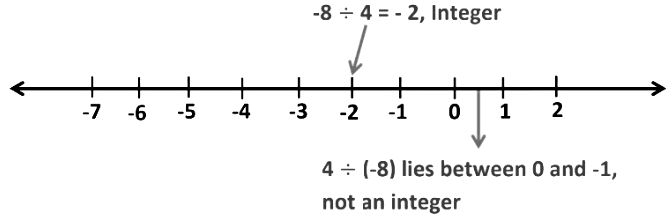
2. Commutative Property
If a and b are two integers, a ÷ b ≠ b ÷ a 3. Associative Property
3. Associative Property
For any 3 integers a, b and c, (a ÷ b) ÷ c ≠ a ÷ (b ÷ c)


4. Division of 0 by any integer
If a is any integer other than zero, then a ÷ 0 is not defined but 0 ÷ a = 0,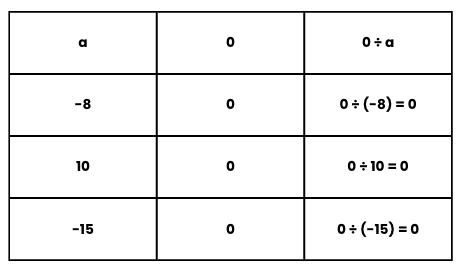
5. Division by 1
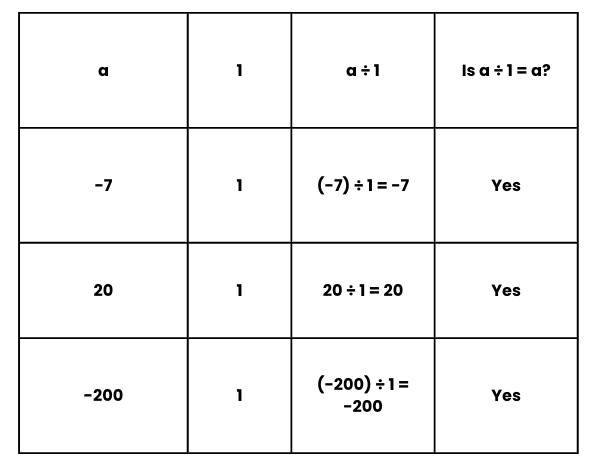
If a is an integer, then a ÷ 1 = a
Example 1: Fill in the blanks
(i) ____ ÷ 25 = 0
If we divide 0 by any integer, the result is always zero.
So, 0 ÷25 = 0
(ii) (-206) ÷ _____ = 1
If we divide any -206 by -206, the result is one.
(-206) ÷ (-206) = 1
(iii) _____ ÷ 1 = -87
If any integer is divided by 1 the result is the same integer.
(-87) ÷ 1 = -87
|
77 videos|386 docs|39 tests
|
FAQs on Integers Class 7 Notes Maths Chapter 1
| 1. What are negative numbers and how are they represented on a number line? |  |
| 2. How do you add integers, including negative numbers? |  |
| 3. What are the rules for subtracting integers? |  |
| 4. What are some properties of addition and subtraction of integers? |  |
| 5. How do you multiply integers, and what are the properties associated with it? |  |

















