Intro to Related Rates Chapter Notes | Calculus AB - Grade 9 PDF Download
By utilizing the concept of the rate of change, we can apply derivatives to tackle real-world scenarios, especially in understanding how one quantity changes in relation to another. This approach is known as related rates in AP Calculus AB.
Using Derivative Rules
Related rates involve using derivatives to determine unknown quantities based on other known quantities and their rates of change. Typically, these problems are framed concerning time.
Quantity of Time
To effectively solve related rate problems, various derivative rules must be employed, depending on the specifics of the problem and which quantities are known or unknown. This includes applying the Chain Rule, the Product Rule, and the Quotient Rule. For detailed explanations, you can refer to our earlier study guides on these rules, found in unit two, linked here.
How to Solve Related Rate Problems
Below is a step-by-step guide for tackling related rates problems:
- Determine Quantities from the Problem
Identify both known quantities, which are explicitly given in the problem, and unknown quantities that must be discovered. - Model the Relationship Between Quantities
This is achieved through a formula. It's crucial to replace any quantities mentioned in the problem that are not directly related to the unknown quantity being solved for, in order to simplify the formula when taking its derivatives. - Apply Derivative Rules with Respect to the Unknown Quantity
After establishing a formula that captures all relevant quantities from the problem, apply the appropriate derivative rules to derive the equation, along with its quantities and their rates of change. Remember, the variables in the formula must be differentiated WITH RESPECT to the same independent variable you are solving for (commonly this is time).
WITH RESPECT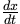
Substitute Known Quantities into the Derived Equation & Solve for Remaining Quantities
This process will simplify the equation, allowing algebraic methods to determine the values of the unknown quantities.
Another important tip for solving related rates problems is to sketch or model the problem and label the quantities provided in the question. This visual aid not only enhances understanding but also assists in identifying the necessary formula for finding the unknown quantities.
Drawing/Modeling Out the Problem and Labeling the Quantities
This may seem overwhelming, so let’s work through a couple of examples to apply this knowledge!
Related Rates Practice
Below are two practice problems to help you become familiar with related rates.
Practice Example #1
Let's begin with a straightforward problem and gradually increase the difficulty!
Suppose an oil spill occurs, spreading in a circular pattern. If the radius of the spill increases at a constant rate of 3 m/s, how fast is the area of the spill increasing when the radius is 30 m?
Circular Constant Rate The Area Increasing
To approach this problem, we can illustrate or model the situation:
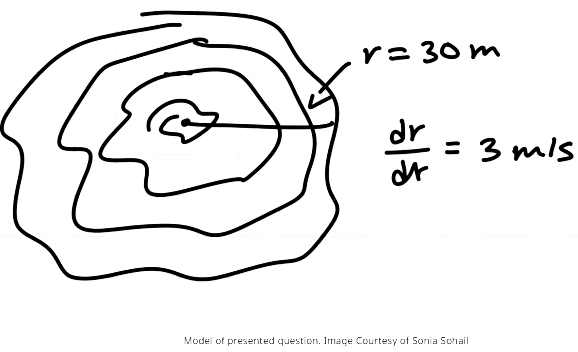 Notice how the radius and its rate of change are clearly labeled in the above illustration. Labeling your quantities in relation to the image is an excellent strategy to identify the known and unknown quantities of the problem. Here, we observe that the known quantities are a radius of 30 meters and a rate of change of the radius with respect to time, denoted as
Notice how the radius and its rate of change are clearly labeled in the above illustration. Labeling your quantities in relation to the image is an excellent strategy to identify the known and unknown quantities of the problem. Here, we observe that the known quantities are a radius of 30 meters and a rate of change of the radius with respect to time, denoted as 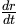 m/s is 3 meters per second (m/s).
m/s is 3 meters per second (m/s).
Since we need to find the area at a specific radius and its rate of change, we can model the relationship using the area formula for a circle:
Given that the problem asks for how fast the area increases at a particular radius (when ( r = 30)), we can express this as “the rate of change of area with respect to time,” denoted 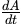 .
.
Now that we know what quantity we are seeking, we can differentiate the formula with respect to time. Using implicit differentiation, we find:
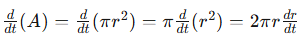
This can be simplified to:
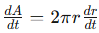
At this point, you may notice we have most of the quantities present in this derivative, allowing us to substitute our known values and solve for the unknown quantity. Be sure to include the units!

Thus, our final answer is 180πm2 /s
Practice Example #2
Here is another problem:
Suppose a 15 ft tall ladder is leaning against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 5 ft/s, how quickly is the top of the ladder sliding down when the bottom of the ladder is 9 ft away from the wall?
At first glance, this problem may seem less straightforward than the previous one. This is a classic "ladder" problem. To grasp what we need to find, it’s helpful to draw or model the situation, using the quantities provided:
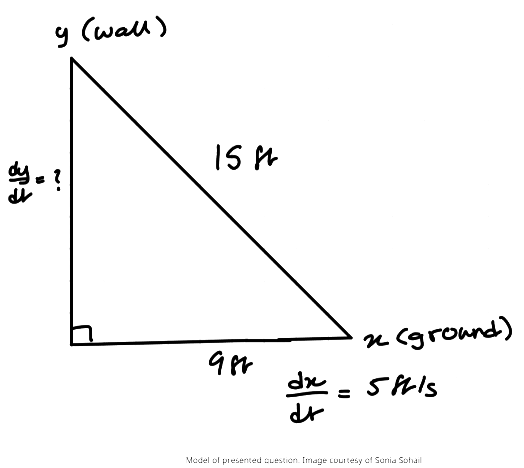
Here, we visualize the ladder leaning against the vertical y-axis, while the bottom of the ladder reaches the horizontal x-axis. This forms a right triangle, and since we know the length of the ladder (the hypotenuse) and one side's length, we can apply the Pythagorean Theorem to model the relationship between the lengths of the wall, the ground, and the ladder.
x2 + y2 = 225
Now that we have a formula that models our scenario, we see that our unknown quantity is the rate of change in (y) because as the ladder slides away from the wall (increasing the x-value), the height of the ladder against the wall decreases. This is denoted as  . We can use implicit differentiation on the formula to find the rates of change for all quantities with respect to time:
. We can use implicit differentiation on the formula to find the rates of change for all quantities with respect to time: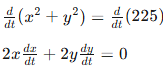
At this point, you might realize that while we have values for most quantities in this derivative, we still need to find (y). You may feel confused, but all you need to do is calculate (y) using the original formula.
Given that (x = 9) ft, we can find the value of (y) by: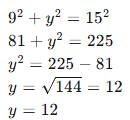
Now that we have the value of (y), we can return to our derivative and substitute the known values to solve for 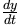 :
: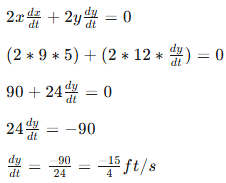
By substituting the known quantities into the equation, we can use algebra to solve for 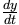 , which
, which 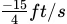 gives us the answer!
gives us the answer!
Closing
By applying the rules of differentiation, related rates represent one method of utilizing calculus to address real-world problems. In the forthcoming guide, we will offer a new set of steps along with additional practice questions, empowering you to choose the technique that suits you best!
Key Terms to Review
- Derivative with respect to time: This derivative measures how a quantity changes over time, illustrating the speed of change for a variable at any given instant.
- Dx/dt: The notation dx/dt represents the derivative of x with respect to t. It measures the rate at which x is changing with respect to time.
- Dy/dt: The notation dy/dt represents the derivative of a function y with respect to the independent variable t. It measures the rate at which y is changing with respect to t.
- Pythagorean Theorem: This theorem states that, in a right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides.
|
26 videos|75 docs|38 tests
|
FAQs on Intro to Related Rates Chapter Notes - Calculus AB - Grade 9
| 1. What are related rates in calculus? |  |
| 2. How do you approach a related rates problem? |  |
| 3. Can you give an example of a related rates problem? |  |
| 4. What is the significance of the Pythagorean theorem in related rates problems? |  |
| 5. How do I differentiate an area formula with respect to time? |  |















