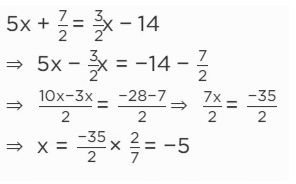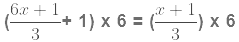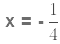Linear Equations in One Variable Class 8 Notes Maths Chapter 2

Algebraic Expressions

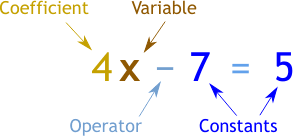
Any expression involving constant, variable and some operations like addition, multiplication etc is called Algebraic Expression. 
For example, 5x and 2x−3.

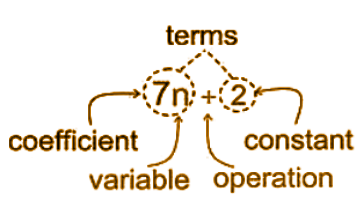
• A variable is an unknown number and generally, it is represented by a letter like x, y, n etc.
• Any number without any variable is called Constant.
• A number followed by a variable is called the Coefficient of that variable.
• A term is any number or variable separated by operators.

Equation

A statement which says that the two expressions are equal is called Equation.

Some expressions have more than one variable, like 2xy+5, but when forming linear equations, we stick to one variable and ensure the variable’s highest power is 1. 
For example, 2x+1 is linear, but x² +1 isn’t. In this chapter, we’ll focus on linear equations in one variable, building on what you’ve already learned. 

Linear Equation in One Variable

A linear equation in one variable is a special type of equation that has the following features:

• As the name suggests, it has only one variable, usually denoted by x, y, or z.
• Now what does linear means? It means that the variable has a power of 1, which means it is not raised to any other exponent like 2, 3, etc. 
• Example: 3x + 4 = 10 is a linear equation but x²- 7 = 3 is not a linear equation, because here x is raised to the power of two.
  
  
  

Left Hand Side (LHS) = 3x + 4 and Right Hand Side (RHS) = 10 

For x = 2,  Let's calculate LHS and RHS: 

LHS = 3(2) + 4  = 6 + 4  = 10 

RHS = 10 

Since LHS = RHS, 

Therefore, x = 2 is the solution to the equation. 

Clear all your Class 8 doubts with EduRev Join for Free

Join for Free

Constant

A constant is a value or number that never changes in an expression and it’s constantly the same.

Variable

A variable is a letter representing some unknown value. Its value is not fixed, it can take any value. On the other hand, the value of a constant is fixed. For example, in the expression, 3x+4, 3 and 4 are the constants and x is a variable.

Coefficient

A coefficient is any number or numerical value being multiplied to a variable. 

Terms

A multiplication of constants and variables, is called an algebraic term. For example, 10x, 5y, 3z, x etc. are all algebraic terms.

Methods for solving linear equation                     

Download the notes Chapter Notes: Linear Equations in One Variable

Download as PDF

Download as PDF

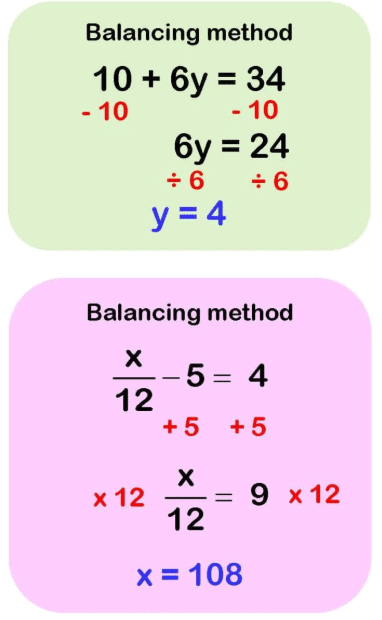
1) Balancing Method

The value of the left-hand side remains equal to the value of the right-hand side if,

• The same number is added to both sides of the equation.
• The same number is subtracted from both sides of the equation.
• Both sides of the equation are multiplied by the same number.
• Both sides of the equation are divided by the same number. 

2) Transposing Method

Transposing means moving to the other side. When a number is transposed from one side to the other side, its sign changes. Transposition of a number has the same effect as adding the same number to (or subtracting the same number from) both the sides.

Take a Practice Test Test yourself on topics from Class 8 exam

Practice Now

Practice Now

Solving equation having variables on both sides

We have seen equations such as 2x-3 = 7, 4y = 2 or 4+3y = 7 that have linear expressions on the one side and numbers on the other side but this might not be the case always.
Both sides could have expressions with variables.
Let us look at some of the examples.

Example 1: Solve 2x – 4 = x + 2

Sol. We have 2x – 4 = x + 2

we get

2x = x + 2 + 4

2x = x + 6

2x – x = x + 6 – x (subtracting x from both sides)

x = 6 is the required answer.

Example 2 : Solve 5x + 7/2 = 3/2x -14, then x= ?

Sol.

Reducing Equations to Simpler Form

Example 3: Solve

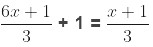
Sol. Multiplying both sides by 6, we get

2 (6x + 1) + 6 = x – 3

12x + 2 + 6 = x –3

12x + 8 = x – 3

12x – x + 8 = – 3

11x + 8 = – 3

11x = –3 – 8

11x = –11

x = – 1

Example 4: Solve the equation: $12(y-3)-4(y-7)+6(y+5)=0$

$\mathrm{<strong\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; inherit;\; font-weight:\; 700;\; word-break:\; break-word;\; font-size:\; 20px;\; color:\; black;\; line-height:\; 1.8;">Sol.</strong>}\mathrm{ 12y}-36-4y+28+6y+30=0$

Combine like terms:

$(12y-4y+6y)+(-36+28+30)=0$

Isolate $\mathrm{y:}$

$14y=-22$

Divide both sides by 14 to solve for $y$

$y=\frac{-}{\mathrm{22/}}=\frac{-}{11}$

Example 5: Solve 

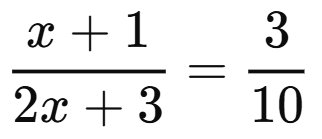
Sol. Here, the given equation is not in linear forms.
On cross multiplying, we get
10(x+1) = 3(2x + 3)

So it gets converted into the linear form.

Now, 10x + 10 = 6x + 9

Transposing 10 and 6x to the other side, we get

10x – 6x = 9 – 10

4x = -1

Dividing both sides by 4, we get

$=\; \backslash frac\{-22\}\{14\}\; =\; \backslash frac\{-11\}\{7\}$$y\; =\; \backslash frac\{-11\}\{7\}$