Class 6 Exam > Class 6 Notes > Mathematics Class 6 ICSE > Chapter Notes: Linear Equations in One Variable
Linear Equations in One Variable Chapter Notes | Mathematics Class 6 ICSE PDF Download
Introduction
Imagine you're on a treasure hunt, and the map gives you clues in the form of equations! Linear equations in one variable are like simple puzzles where you need to find the value of a single unknown, such as x or y. These equations are called "linear" because they represent a straight line when graphed, and they only involve the variable raised to the power of one. This chapter is all about turning words into math, moving terms around, and solving these puzzles step-by-step to uncover the hidden number. Let’s dive into this exciting world of equations and learn how to crack them!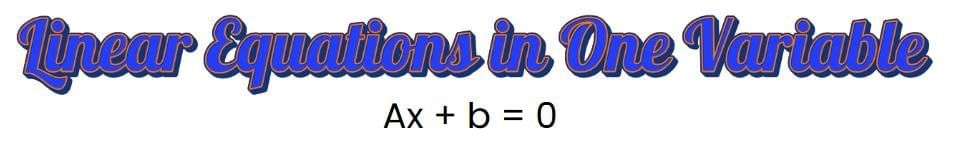
To Write a Given Statement in Algebraic Form
- Convert a word statement into a mathematical expression by using letters for unknowns and symbols for operations.
- Identify key phrases like "added to," "subtracted from," "multiplied by," or "divided by" to assign the correct operations.
- Use a variable (like x or y) to represent the unknown number.
- Ensure the equation reflects the relationship described in the statement.
Example: Seven added to y gives 20.
Solution: The phrase "seven added to y" means 7 + y, and "gives 20" means equals 20. So, the algebraic form is 7 + y = 20.
Solution: The phrase "seven added to y" means 7 + y, and "gives 20" means equals 20. So, the algebraic form is 7 + y = 20.
To Write a Statement for a Given Algebraic Form
- Translate a mathematical equation into a word statement by interpreting the symbols and variables.
- Replace the variable with words like "a number" or the variable’s name.
- Describe operations like + (added to), - (subtracted from), × (multiplied by), or ÷ (divided by) in words.
- Ensure the statement clearly conveys the equation’s meaning.
Example: 7 - x = 5
Solution: The equation means "x subtracted from 7 gives 5."
Solution: The equation means "x subtracted from 7 gives 5."
Linear Equations in One Variable
- An equation is a statement showing that two expressions are equal, with an equals sign (=) between them.
- A linear equation has variables with the highest power of one (no x2 or higher).
- A linear equation in one variable involves only one unknown, like x or n.
- Examples include 2n + 3 = 7 or x + 5 = 4x.
Example: 2n + 3 = 7 is a linear equation in one variable because it involves only n with power one.
Properties of Equations
- Addition Property: Adding the same number to both sides keeps the equation balanced.
Formula: If x = y, then x + z = y + z. - Subtraction Property: Subtracting the same number from both sides keeps the equation balanced.
Formula: If x = y, then x - z = y - z. - Multiplication Property: Multiplying both sides by the same number keeps the equation balanced.
Formula: If x = y, then x × z = y × z. - Division Property: Dividing both sides by the same non-zero number keeps the equation balanced.
Formula: If x = y and z ≠ 0, then x ÷ z = y ÷ z.
Example: If x = 5, then adding 3 to both sides gives x + 3 = 5 + 3, or x + 3 = 8.
Transposition of Terms of an Equation
- Move a term from one side of the equation to the other by changing its sign (e.g., + becomes -, × becomes ÷).
- Addition becomes subtraction, subtraction becomes addition, multiplication becomes division, and division becomes multiplication when transposing.
- This simplifies the equation by grouping similar terms.
Example 1: x + 5 = 7
Solution: Transpose 5 to the other side: x = 7 - 5, so x = 2.
Solution: Transpose 5 to the other side: x = 7 - 5, so x = 2.
- The solution is the value of the variable that makes the equation true.
- Substitute the solution into the equation to verify it satisfies both sides.
Example 2: For 3x - 5 = -2, x = 1 is the solution.
Verification: Substitute x = 1: 3 × 1 - 5 = 3 - 5 = -2, which equals the right-hand side.
Verification: Substitute x = 1: 3 × 1 - 5 = 3 - 5 = -2, which equals the right-hand side.
Solving Linear Equations in One Variable
- Move all terms with the variable to one side using transposition.
- Move all constant terms to the other side.
- Simplify the equation by combining like terms.
- Divide both sides by the coefficient of the variable to find its value.
Example : Solve y + 3 = 1 - y
Solution:
Solution:
- Transpose -y to the left: y + y + 3 = 1
- Simplify: 2y + 3 = 1
- Transpose 3 to the right: 2y = 1 - 3
- Simplify: 2y = -2
- Divide by 2: y = -2 ÷ 2 = -1
Verification of the Solution
- After solving, check the solution by substituting the variable’s value into the original equation.
- Calculate the left-hand side (LHS) and right-hand side (RHS) separately.
- If LHS equals RHS, the solution is correct.
- This step ensures no mistakes were made during solving.
Example: Solve and verify 4(x + 2) = 2x + 5
Solution:
Solution:
- Expand: 4x + 8 = 2x + 5
- Transpose 2x to the left: 4x - 2x + 8 = 5
- Simplify: 2x + 8 = 5
- Transpose 8: 2x = 5 - 8
- Simplify: 2x = -3
- Divide by 2: x = -3 ÷ 2 = -3/2
- Verification: Substitute x = -3/2 in LHS: 4(-3/2 + 2) = 4(1/2) = 2. In RHS: 2(-3/2) + 5 = -3 + 5 = 2. Since LHS = RHS, the solution x = -3/2 is correct.
Word Problems
- Read the problem carefully to understand the situation.
- Assign a variable to the unknown quantity.
- Form an equation based on the given conditions.
- Solve the equation using the steps for linear equations.
- Verify the solution by checking if it fits the problem’s conditions.
Example: A number when decreased by 12 gives 30. Find the number.
Solution:
Solution:
- Let the number be x.
- Form the equation: x - 12 = 30
- Transpose -12: x = 30 + 12
- Simplify: x = 42
- The number is 42.
Solved Examples
Example 1: Solve 4(x + 2) = 2x + 5
Solution:
Solution:
- Expand: 4x + 8 = 2x + 5
- Transpose 2x to the left: 4x - 2x + 8 = 5
- Simplify: 2x + 8 = 5
- Transpose 8: 2x = 5 - 8
- Simplify: 2x = -3
- Divide by 2: x = -3 ÷ 2 = -3/2
- Verification: Left side: 4(-3/2 + 2) = 4(1/2) = 2; Right side: 2(-3/2) + 5 = -3 + 5 = 2. Since both sides equal, x = -3/2 is correct.
Example 2: A man is 29 years older than his daughter. If the sum of their ages is 85 years, find their present ages.
Solution:
Solution:
- Let the daughter’s age be x years.
- Man’s age is x + 29 years.
- Form the equation: x + (x + 29) = 85
- Simplify: 2x + 29 = 85
- Transpose 29: 2x = 85 - 29 = 56
- Divide by 2: x = 56 ÷ 2 = 28
- Daughter’s age is 28 years, man’s age is 28 + 29 = 57 years.
The document Linear Equations in One Variable Chapter Notes | Mathematics Class 6 ICSE is a part of the Class 6 Course Mathematics Class 6 ICSE.
All you need of Class 6 at this link: Class 6
|
44 videos|201 docs|24 tests
|
FAQs on Linear Equations in One Variable Chapter Notes - Mathematics Class 6 ICSE
| 1. What is a linear equation in one variable? |  |
Ans. A linear equation in one variable is an equation that can be expressed in the form ax + b = 0, where 'a' and 'b' are constants, and 'x' is the variable. The highest exponent of the variable is 1, which makes it a linear equation.
| 2. How can I write a verbal statement in algebraic form? |  |
Ans. To write a verbal statement in algebraic form, identify the key components of the statement, such as quantities, operations (addition, subtraction, multiplication, division), and relationships. Translate these components into mathematical symbols. For example, the statement "five more than a number x" can be written as x + 5.
| 3. What are the properties of equations that are important for solving linear equations? |  |
Ans. The key properties of equations include the addition property (you can add the same value to both sides of the equation), the subtraction property (you can subtract the same value from both sides), the multiplication property (you can multiply both sides by the same non-zero value), and the division property (you can divide both sides by the same non-zero value). These properties help maintain the equality of the equation while manipulating it.
| 4. How do I verify the solution of a linear equation? |  |
Ans. To verify the solution of a linear equation, substitute the value obtained back into the original equation. If both sides of the equation are equal after substitution, then the solution is correct. If they are not equal, the solution is incorrect.
| 5. What are some common word problems involving linear equations? |  |
Ans. Common word problems involving linear equations include scenarios like calculating distances, finding ages, and determining costs. For example, a problem may state, "If a book costs x dollars and you have 20 dollars, how many books can you buy?" This can be represented as the equation x * number of books = 20, leading to a solution for the number of books.
Related Searches





















