Mathematics of Finance Chapter Notes | Quantitative Aptitude for CA Foundation PDF Download
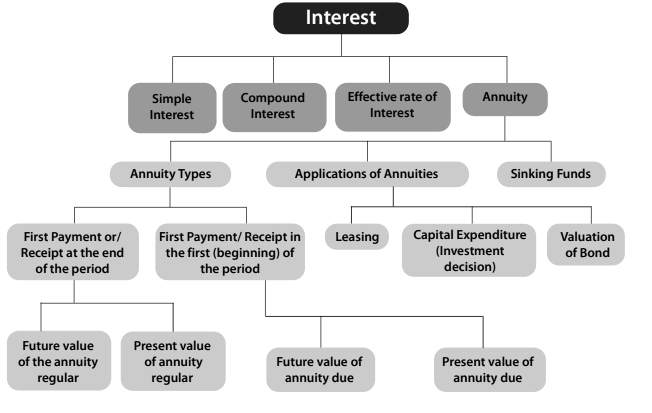
Chapter Overview
Introduction
In our daily lives, we earn money by meeting our basic needs like housing, food, clothing, education, and entertainment. However, there are times when we need to spend money on unexpected events or big purchases, such as a family wedding, buying a house, starting a business, or buying a car. Some people can save up for these expenses, but many others have to borrow money.
Borrowing Money
Money can be borrowed from various sources:
- Friends: If you borrow from a friend, it might be interest-free.
- Money Lenders: These are individuals or businesses that lend money, usually at a higher interest rate.
- Banks: Banks lend money but charge interest, which is a fee for using their money.
Saving and Investing
After meeting their needs, some people have leftover money that they can save. This saved money can be invested in various ways, such as:
- Debentures: These are debt instruments that companies issue to raise money, and investors earn interest on them.
- Lending to Others: People can lend money to others and charge interest.
- Bank Deposits: Depositing money in a bank account can earn interest over time.
Understanding Interest
Interest is a common term that refers to the price a borrower pays for using a lender’s money. It is an important concept in borrowing and lending money. We will learn more about interest and related terms later.
Why Lenders Charge Interest
- Time Value of Money: The value of money changes over time. A certain amount of money today is worth more than the same amount in the future. This is because money can earn interest when invested. Therefore, lenders prefer to receive money now rather than later, and they charge interest to compensate for this time difference.
- Opportunity Cost: When lenders choose to lend their money, they miss out on other potential investments. If they decide to lend their money, they incur an opportunity cost because they could have gained returns from other investments instead.
- Inflation: In many economies, inflation decreases the purchasing power of money over time. This means that the same amount of money will buy fewer goods in the future than it does now. Borrowers must pay interest to cover this loss in value due to inflation.
- Liquidity Preference: People generally prefer to keep their resources in forms that can be easily converted into cash. This preference for immediate access to funds leads lenders to charge interest, as they must wait to get their money back.
- Risk Factor: There is always a possibility that the borrower may not repay the loan, leading to a loss for the lender. The level of risk associated with a loan affects the interest rate; lenders typically charge a higher interest rate (risk premium) for loans that carry more risk.
Definition Of Interest And Some Other Related Terms
Interest- Interest is the cost a borrower pays for using a lender's money.
- When you borrow or lend money for a certain period, you pay or receive more than the original amount.
- This extra amount is called interest.
- For example, if you borrow ₹50,000 for a year and repay ₹55,000, the difference of ₹5,000 is the interest you paid.
Principal
- The principal is the original amount of money that is borrowed or lent.
- If you invest money, the initial amount you invest is also referred to as the principal.
- For instance, if you borrow ₹50,000 for one year, that ₹50,000 is the principal.
- Similarly, if you deposit ₹20,000 in a bank for a year, that ₹20,000 is the principal.
Rate of Interest
- The rate of interest is how much interest is charged over a specific period, usually calculated per year.
- It is typically expressed as a percentage.
- For example, if you invest ₹20,000 in a bank account for one year with a 5% interest rate, you will earn ₹5 for every ₹100 of the principal in a year.
Accumulated Amount (or Balance)
- The accumulated amount is the total value of your investment after a certain period.
- It is the sum of the principal and the interest earned.
- For example, if you deposit ₹50,000 in a bank for one year at a 5% interest rate, you will earn ₹2,500 in interest.
- After one year, you will receive ₹52,500 (which is the principal plus interest). Here, ₹52,500 is the accumulated amount.
- The accumulated amount is also known as the balance.
Now we can discuss the method of computing interest. Interest accrues as either simple interest or compound interest. We will discuss simple interest and compound interest in the following paragraphs:
Simple Interest and Compound Interest
Simple Interest
- Simple interest is the interest calculated on the principal amount for the entire duration of borrowing.
- It is computed based on the outstanding principal balance and does not take into account any interest that may have been previously earned.
- In other words, interest is not paid on interest accrued during the term of the loan.
Formula for Simple Interest
I = Pit
A = P + I
A = P(1 + it)
I = A – P
Where:
- A. Accumulated amount (final value of an investment)
- P. Principal (initial value of an investment)
- i. Annual interest rate in decimal
- I. Amount of Interest
- t. Time in years
Example 1: Calculating Interest on ₹ 2000 at 6% Simple Interest for
To find the interest earned on ₹ 2000 at a simple interest rate of 6% for 2 years, we use the formula:
I = P × i × t
I = 2000 × (6/100) × 2
I = ₹ 240
Example 2: Sania's Deposit of ₹ 50,000 at 5.5% Simple Interest for 2 Years
Sania deposited ₹ 50,000 in a bank for 2 years at a simple interest rate of 5.5% per annum. To calculate the interest earned, we apply the same formula:
I = P × i × t
I = 50000 × (5.5/100) × 2
I = ₹ 5,500
Example 3: Calculating the Final Value of Sania's Investment
To determine the final value of Sania's investment, we can use either of the following methods:
A = P(1 + it)
A = P + I
Using the first method:
A = 50000 × (1 + (5.5/100) × 2)
A = 50000 × (1 + 0.11)
A = 50000 × (111/100)
= ₹ 55,500
Using the second method:
A = P + I
A = 50000 + 5500
A = ₹ 55,500
Example 4: Sachin's Deposit of ₹ 1,00,000 at 6% Simple Interest for 2 Years
(a) To calculate the interest earned by Sachin, we use the formula:
I = P × i × t
I = 1,00,000 × (6/100) × 2
I = ₹ 12,000
(b) To find the final value of Sachin's deposit, we can use either of the following methods:
A = P + I
A = P(1 + it)
Using the first method:
A = P + I
A = 1,00,000 + 12,000
A = ₹ 1,12,000
Using the second method:
A = P(1 + it)
A = 1,00,000 × (1 + (6/100) × 2)
A = 1,00,000 × (1 + 0.12)
A = 1,00,000 × (112/100)
A = ₹ 1,12,000
Example 5: Finding the Rate of Interest
Given that the amount owed after 6 months is ₹ 1,050 and the borrowed amount is ₹ 1,000, we can use the formula:
A = P + Pit
1,050 = 1,000 + 1,000 × i × (6/12)
50 = 500i
i = 1/10 = 10%
Example 6: Finding the Period of Rahul's Investment
Given that Rahul invested ₹ 70,000 at a simple interest rate of 6.5% per annum and received ₹ 85,925 at the end of the term, we can use the formula:
A = P(1 + it)
85,925 = 70,000 × (1 + (6.5/100) × t)
85,925/70,000 = (100 + 6.5t)/100
85,925 × 100/70,000 - 100 = 6.5t
22.75 = 6.5t
t = 3.5 years
Example 7: Finding Kapil's Initial Deposit
Given that Kapil received ₹ 1,01,500 at the end of 7 ½ years at a simple interest rate of 6% per annum, we can use the formula:A = P(1 + it)
1,01,500 = P × (1 + (6/100) × 15/2)
1,01,500 = P × (145/100)
P = 1,01,500 × 100/145
P = ₹ 70,000
Example 8: Finding the Rate of Interest Percent Per Annum
Given that a sum of ₹ 46,875 was lent out at simple interest and at the end of 1 year 8 months the total amount was ₹ 50,000, we can use the formula:A = P(1 + it)
50,000 = 46,875 × (1 + i × 1 12)
50,000/46,875 = 1 + 5 3 i
(1.067 – 1) × 3/5 = i
i = 0.04
rate = 4%
Example 9: Finding the Principal and Rate of Interest
Given that a sum of money amounts to ₹ 6,200 in 2 years and ₹ 7,400 in 3 years, we can use the formula:
A = P(1 + it)
6,200 = P(1 + i × 2)
7,400 = P(1 + i × 3)
By solving these equations, we can find that the principal is ₹ 3,800 and the rate of interest is 31.58%.
Example 10: Finding the Time for a Sum of Money to Triple Itself
Given that a sum of money doubles itself in 10 years, we can use the formula:10 years = T/2
T = 20 years
Therefore, the number of years it would triple itself is 20 years.
Compound Interest
- We have learned about simple interest. Simple interest is calculated when the principal amount stays the same throughout the entire time period.
- However, the way banks, insurance companies, and other lenders calculate interest is different in practice.
- To understand this method, let's look at an example:
- Imagine you deposit ₹ 50,000 in ICICI Bank for 2 years at an interest rate of 7% per annum, compounded annually.
Interest For The First Year
To calculate the interest for the first year, we use the formula:
I = P * i * t
Where:
- P = Principal amount (₹ 50,000)
- i = Interest rate (7/100)
- t = Time (1 year)
Calculating:
Interest = ₹ 50,000 * 7/100 * 1 = ₹ 3,500
Interest For The Second Year
For the second year, the principal used to calculate interest is the initial deposit plus the interest from the first year.
So, the principal for the second year becomes:
₹ 50,000 + ₹ 3,500 = ₹ 53,500
Now, we calculate the interest for the second year:
Interest = ₹ 53,500 * 7/100 * 1 = ₹ 3,745
Total Interest
The total interest earned over the two years is:
Total interest = Interest from the first year + Interest from the second year
Total interest = ₹ 3,500 + ₹ 3,745
Total interest = ₹ 7,245
This interest is ₹ 245 more than the simple interest on ₹ 50,000 for two years at 7% per annum. The extra interest is because the principal amount for the second year was greater than that of the first year. The interest calculated in this way is known as compound interest. We can define compound interest as the interest that builds up when the earnings for each specific time period are added to the principal, which increases the principal amount used for calculating future interest.
Example 11:
- Saina deposited ₹ 1,00,000 in a nationalized bank for three years.
- If the interest rate is 7% per annum, calculate the interest the bank will pay Saina after three years with annual compounding.
- Also, calculate the total amount at the end of the third year.
Solution:
Principal for the first year: ₹ 1,00,000Principal for the second year:
- Interest for the first year:
- Calculation: Principal × rate × time
- ₹ 1,00,000 × 7/100 × 1 = ₹ 7,000
Interest for the second year:
- Calculation: Principal for first year + Interest for first year
- ₹ 1,00,000 + ₹ 7,000 = ₹ 1,07,000
Principal for the third year:
- Calculation: ₹ 1,07,000 × 7/100 × 1
- ₹ 7,490
Interest for the third year:
- Calculation: Principal for second year + Interest for second year
- ₹ 1,07,000 + ₹ 7,490 = ₹ 1,14,490
Compound interest at the end of the third year:
- Calculation: ₹ 1,14,490 × 7/100 × 1
- ₹ 8,014.30
Total amount at the end of the third year:
- Calculation: ₹ 7,000 + ₹ 7,490 + ₹ 8,014.30
- ₹ 22,504.30
- Calculation: Principal + Compound interest
- ₹ 1,00,000 + ₹ 22,504.30
- ₹ 1,22,504.30
Difference Between Simple Interest and Compound Interest
- In simple interest, the principal amount remains the same throughout the entire period. This means that the interest is calculated only on the original principal.
- In compound interest, the principal amount changes at the end of each specified period because the interest earned is added to the principal. This means that interest is calculated on the new principal, which includes the previously earned interest.
- For the same principal, rate, and time period, compound interest is generally greater than simple interest.
Conversion period
- The earlier example showed that interest was calculated on a yearly basis, meaning it was compounded annually.
- In reality, it’s not always the case that interest is compounded once a year.
- For instance, many banks often compound interest twice a year, which is known as half-yearly or semi-annually.
- This means that interest is calculated and added to the principal amount every six months.
- Some financial institutions choose to compound interest quarterly, which is four times a year.
- The time period after which interest is added to the principal is called the conversion period.
- When interest is compounded every six months, the conversion period is six months.
- In this case, there would be two conversion periods in a year.
- If a loan or deposit lasts for five years, the total number of conversion periods would be ten.
Typical conversion periods are given below:

Formula for compound interest
Take the principal amount as P, the interest rate per conversion period as i (in decimal), and the total number of conversion periods as n.- The amount accumulated after n payment periods is An.
- At the end of the first payment period, the amount is calculated as:
- A1 = P + P * i = P (1 + i)
- At the end of the second payment period, the amount becomes:
- A2 = A1 + A1 * i = A1 (1 + i)
- This simplifies to: A2 = P (1 + i)(1 + i) = P (1 + i)2
- At the end of the third payment period, the amount is:
- A3 = A2 + A2 * i = A2 (1 + i)
- This further simplifies to: A3 = P (1 + i)2 (1 + i) = P (1 + i)3
- Continuing this pattern, we can express the amount after nperiods as:
- An = An-1 + An-1 * i = An-1 (1 + i)
- This leads to: An = P (1 + i)n-1 (1 + i) = P (1 + i)n
- Therefore, the total amount An on a principal P after n conversion periods at an interest rate i (in decimal) is: An = P (1 + i)n
- Here, i represents the annual interest rate divided by the number of conversion periods per year.
- The interest earned can be calculated as:
- Interest = An - P = P (1 + i)n - P
- Which simplifies to: Interest = P [(1 + i)n - 1]
- The total number of conversions, n, is calculated as the total time t multiplied by the number of conversions per year.
- Note: You can easily compute these amounts using a calculator. Additionally, compound interest tables for various annual rates are available, including:
(a) Annual compounding
(b) Monthly compounding
(c) Daily compounding
Example 12: If you invest ₹2,000 at an annual interest rate of 10%, what will the total amount be after two years with different compounding methods?
Solution:₹
(a) Compounding Annually:
- Principal amount P = ₹2,000.
- Since interest is compounded once a year, the number of compounding periods n over 2 years is 2.
- The interest rate per compounding period i is 0.10.
- The formula for the amount A is: An = P (1 + i)n.
- Calculating the total: A2 = ₹2,000 (1 + 0.1)2.
This equals ₹2,000 × (1.1)2.
Which simplifies to ₹2,000 × 1.21 = ₹2,420.(b) Compounding Semi-Annually:
- Here, n = 2 × 2 = 4 (because interest is compounded twice a year).
- The interest rate per period i = 0.1 / 2 = 0.05.
- Applying the formula: A4 = 2,000 (1 + 0.05)4.
This calculates to ₹2,000 × 1.2155 = ₹2,431.(c) Compounding Quarterly:
- For quarterly compounding, n = 4 × 2 = 8.
- The interest rate per period i = 0.1 / 4 = 0.025.
- Using the formula: A8 = 2,000 (1 + 0.025)8.
This results in ₹2,000 × 1.2184 = ₹2,436.80.(d) Compounding Monthly:
- In this case, n = 12 × 2 = 24 (because it compounds every month).
- The interest rate per period i = 0.1 / 12 = 0.00833.
- Calculating the amount: A24 = 2,000 (1 + 0.00833)24.
This gives ₹2,000 × 1.22029 = ₹2,440.58.
Example 13: Calculate the total amount and the interest earned on ₹ 1000 at 6% interest, compounded twice a year for 6 years.
For this calculation, we know that (1 + i)n = 1.42576 where i = 3% and n = 12.
Solution:
- Interest Rate (i): 0.06 divided by 2 equals 0.03.
- Number of Compounding Periods (n): 6 years multiplied by 2 equals 12.
- Principal Amount (P):₹ 1,000.
Compound Amount (A12):
- Calculate using the formula: A = P (1 + i)^n.
- Substituting the values: A = ₹ 1,000 (1 + 0.03)12.
- This simplifies to: ₹ 1,000 × 1.42576.
- The result is: ₹ 1,425.76.
Compound Interest:
- To find the interest earned, subtract the principal from the total amount:
- Interest = ₹ (1,425.76 - 1,000).
- This gives us: ₹ 425.76.
Example 14: Calculate the compound interest on ₹ 4,000 for 1½ years at 10% per year, compounded half-yearly.
Solution: The principal amount P is ₹ 4,000.
Since the interest is compounded half-yearly, the total number of compounding periods in 1½ years is 3.
The interest rate for each compounding period (which is 6 months) is calculated as follows:
10% divided by 2 equals 5% (or 0.05 in decimal).
Thus, the total amount A after 3 periods is calculated using the formula:A = P (1 + i)n
A = 4,000(1 + 0.05)3
A = 4,000 × 1.157625 = ₹ 4,630.50
The compound interest is calculated by subtracting the principal from the total amount:
Compound Interest = A - P
Compound Interest = ₹ 4,630.50 - ₹ 4,000
Compound Interest = ₹ 630.50
Finding Principal, Time, and Rate in Compound Interest
- The formula An = P(1 + i)n connects four variables: An, P, i, and n.
- Compound Interest (C.I.) is calculated as C.I. = P (1 + i)n - 1.
- With any three of these four variables known, the fourth can be calculated easily.
Example 15: How much principal will yield a compound interest of ₹ 1,640 at 5% per annum compounded annually for two years?
Solution:
- Since interest is compounded annually, n = 2 and i = 0.05.
- Using C.I. = P (1 + i)n - 1: 1,640 = P(1 + 0.05)2 - 1
- Solving gives P = ₹ 16,000.
Example 16: What annual interest rate compounded annually will double an investment in 7 years?
Solution:
- Let P be the principal, then An = 2P.
- From the formula: 2P = P(1 + i)7
- Thus, 21/7 = (1 + i).
- Calculating gives i = 0.10409, or an interest rate of 10.41% per annum.
Example 17: How long will ₹ 8,000 amount to ₹ 8,820 at 10% interest compounded half-yearly?
Solution:
- Principal P = ₹ 8,000 and i = 5% (or 0.05).
- Using An = P(1 + i)n: 8,820 = 8,000(1 + 0.05)n
- Simplifying gives n = 2, which means the time period is 1 year.
Example 18: What is the interest rate if ₹ 2,00,000 grows to ₹ 2,31,525 in 1.5 years with half-yearly compounding?
Solution:
- Here, P = ₹ 2,00,000 and the number of compounding periods n = 3.
- Applying the formula: 2,31,525 = 2,00,000(1 + i)3
- Solving leads to i = 0.05, which translates to an annual rate of 10%.
Example 19: If ₹ 16,000 is invested at 4% per annum compounded semi-annually, what will it amount to at the end of one year?
Solution:
- The total amount after one year is calculated using An = P(1 + i)n.
- With n = 2 and i = 2% (or 0.02): A2 = 16,000(1 + 0.02)2
- This results in P = ₹ 15,000 as the initial investment.
Example 20: If ₹ 16,000 at 10% compounded semi-annually results in ₹ 18,522, how long was it invested?
Solution:
- Given P = ₹ 16,000 and An = ₹ 18,522, with i = 5% (or 0.05).
- Using the formula: 18,522 = 16,000(1 + 0.05)n
- Solving provides n = 3, indicating an investment period of 3 half-years.
Example 21: A person deposits ₹ 800 at 6% interest compounded quarterly. After six months, he adds enough to invest ₹ 1,000 for six months at the same interest rate. What are the additional amount, maturity value, and total interest earned?
Solution:
- (a) The initial deposit earns interest for two quarters: i = 1.5% = 0.015 and n = 2.
- Compounded amount: 800(1 + 0.015)2 = ₹ 824.18.
- The additional amount invested is ₹ (1,000 - 824.18) = ₹ 175.82.
- (b) The new deposit earns interest for six months: i = 0.5% = 0.005 and n = 6.
- Maturity value: 1,000(1 + 0.005)6 = ₹ 1,030.38.
- (c) Total interest earned is ₹ (24.18 + 30.38) = ₹ 54.56.
Effective Interest Rate
Definition: The Effective Interest Rate (EIR) represents the true annual return on an investment or loan when interest is compounded more than once a year. It is always higher than the nominal interest rate when compounding occurs more frequently.
Formula: The effective interest rate can be calculated using the formula: E = (1 + i)ⁿ - 1 Where: E. Effective interest rate i = Nominal interest rate per period n = Number of compounding periods per year
Example: Let's say you invest ₹10,000 at a nominal interest rate of 6% per annum, compounded semi-annually. To calculate the effective interest rate:
- Convert the nominal rate to a decimal: 6% = 0.06
- Determine the number of compounding periods per year: Semi-annually means n = 2
- Apply the formula: E = (1 + 0.06/2)² - 1 E = (1 + 0.03)² - 1 E = (1.03)² - 1 E ≈ 0.0609 or 6.09%
Interpretation: In this example, the effective interest rate of 6.09% is higher than the nominal rate of 6% because the interest is compounded more frequently. This illustrates how compounding frequency can impact the overall return on an investment.
Examples of Effective Interest Rate:
Example 1: Term Deposit Scheme
A person invests ₹ 5,000 in a Term Deposit Scheme with an interest rate of 6% per annum compounded quarterly. To calculate the interest after one year and the effective rate of interest:
- Principal (P):. 5,000
- Interest Rate (i): 6% p.a. = 0.06 p.a. or 0.015 per quarter
- Number of Compounding Periods (n):.
Calculation:
- Compound Interest (I):. = P [ (1 + i/n) (nt) ] - P I
= ₹ 5,000 [ (1 + 0.015) 4 ] - 5,000. = ₹ 5,000 [ 1.06136355 - 1 ]. = ₹ 5,000 × 0.06136355. ≈ ₹ 306.82
Effective Rate of Interest (E):
- Using I = PEt: 306.82 = 5,000 × E × 1 E = 306.82 / 5000 E = 0.0613 or 6.13%
- Using E = (1 + i/n) ^ n - 1:. = (1 + 0.015) ^ 4 - 1 E = 1.0613 - 1 E = 0.0613 or 6.13%
Example 2: Bank Deposit
An amount of ₹ 20,000 is deposited in a bank for one year at an interest rate of 8% per annum compounded semi-annually. To find the amount of compound interest and effective rate of interest:
- Principal (P):. 20,000
- Interest Rate (i): 8% p.a. = 8/2 % semi-annually = 0.04
- Number of Compounding Periods (n):.
Calculation:
- Compound Interest (I):. = P [ (1 + i/n) (nt) ] - P I
= ₹ 20,000 [ (1 + 0.04) 2 ] - 20,000. = ₹ 20,000 [ 1.0816 - 1 ]. = ₹ 20,000 × 0.0816. = ₹ 1,632
Effective Rate of Interest (E):
- Using I = PEt: 1,632 = 20,000 × E × 1 E = 1,632 / 20,000 E = 0.0816 or 8.16%
- Using E = (1 + i/n) n - 1:. = (1 + 0.04) 2 - 1 E = 0.0816 or 8.16%
Example 3: Investment Comparison
Comparing an investment offering 3% per year compounded monthly with another offering 3.2% per year simple interest.
- Compounded Monthly:. = 3/12 = 0.25% = 0.0025 n = 12 E = (1 + 0.0025) 12 - 1 E = 1.0304 - 1 E = 0.0304 = 3.04%
Conclusion: Since the effective rate of interest (3.04%) is less than 3.2%, the simple interest option of 3.2% per year is the better investment.
Annuity
- An annuity is a financial concept that involves making or receiving regular, fixed payments over a specified period of time.
- To qualify as an annuity, the following criteria must be met:
- Constant Amount: The amount paid or received must remain the same throughout the duration of the annuity.
- Equal Time Intervals: The time intervals between consecutive payments or receipts must be consistent.
Regular Payments: Examples include life insurance premiums, rent, housing loans, and vehicle loans, where a fixed amount is paid regularly, such as monthly or annually.
Fixed Receipts: Instances like pensions or house rent, where a fixed amount is received regularly, also fall under annuities.
Perpetuity: This is a special type of annuity where payments or receipts occur indefinitely, making it impossible to calculate a future value. However, the present value of perpetuity can be determined.
Future Value and Present Value of Annuity: These concepts will be discussed later, focusing on the time value of money in relation to annuities.
Examples of Annuity:
Conclusion
An annuity involves regular, fixed payments or receipts over a specified period, with the same amount and time intervals. Perpetuity is a special case of annuity with indefinite payments or receipts.
Annuity regular and Annuity due/immediate
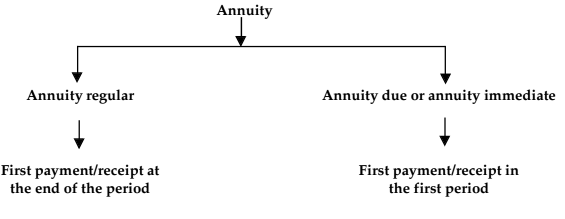
Types of Annuities
Annuities can be categorized into two types based on the timing of the first payment or receipt.
(1) Annuity Regular: In an annuity regular, the first payment or receipt occurs at the end of the first period. For example, consider the following scenario:
Year EndPayments/Receipts (₹)
- I 5,000
- II 5,000
- III 5,000
- IV 5,000
- V 5,000
In this case, the first payment or receipt takes place at the end of the first year, which is why it is classified as an annuity regular.
(2) Annuity Due or Annuity Immediate: An annuity due or annuity immediate occurs when the first receipt or payment is made today, at the beginning of the annuity. For instance, consider the following scenario:
In the Beginning ofPayment/Receipt (₹)
- I year 5,000
- II year 5,000
- III year 5,000
- IV year 5,000
- V year 5,000
In this example, the first receipt or payment is made at the beginning of the first year, which is why this type of annuity is called annuity due or annuity immediate.
Future Value
- Future value refers to how much money an investment will be worth at a later time. It represents the value of today's money after earning interest over time.
- For example, if you invest ₹1,000 in a fixed deposit with an interest rate of 7% per year, at the end of the first year, you will have ₹1,070.
- This total includes your original investment of ₹1,000 and an interest of ₹70.
- Thus, the future value of ₹1,000 invested for one year at 7% is ₹1,070.
- If you decide to invest that ₹1,070for another year, you will want to know how much you will have at the end of the second year.
- At the end of the first year, your amount was ₹1,070.
- If you reinvest this amount, you will calculate it as ₹1,070 multiplied by (1 + 0.07), which equals ₹1,144.90 at the end of the second year.
- Therefore, ₹1,144.90 is the future value of ₹1,000 invested for two years at 7%.
- To find the future value of a single cash investment, you can use the compound interest formula:
- A = P (1 + i)n
- In this formula:
- A = Total amount after interest
- P = Initial investment (principal)
- i = Interest rate per period (in decimal form)
- n = Number of compounding periods
The future value of a single cash flow can be calculated using a specific formula.
In this formula, you can replace A with future value (F) and P with single cash flow (C.F.).
The formula looks like this: F = C.F. (1 + i)n
Here, i represents the interest rate, and n is the number of periods.
This formula helps in understanding how much a single amount of money will grow over time when invested or saved at a certain interest rate.
Future Value of an Investment
Example 25:Consider an investment of ₹ 3,000 made for two years at an annual interest rate of 12%. Let's calculate the future value of this investment.
Solution: The formula for calculating future value is: F = C.F. (1 + i) n
where: F. Future value C.F.. Cash flow = ₹ 3,000
i. rate of interest = 0.12
n. time period = 2 years
Now, substituting the values into the formula:
F = ₹ 3,000 (1 + 0.12) 2= ₹ 3,000 × 1.2544= ₹ 3,763.20
Future Value of an Annuity
To calculate the future value of an annuity, let's consider an example where a constant amount of ₹ 1 is deposited at the end of each year for four years at an interest rate of 6%.
Example: Future Value of an Annuity
When ₹ 1 is deposited at the end of each year for four years at 6% interest, the future value can be calculated using compound interest.
- Year 1: The deposit of ₹ 1 will grow for three years:
A₃ = ₹ 1 (1 + 0.06)³ = ₹ 1.191 - Year 2: The deposit of ₹ 1 will grow for two years:
A₂ = ₹ 1 (1 + 0.06)² = ₹ 1.124 - Year 3: The deposit of ₹ 1 will grow for one year:
A₁ = ₹ 1 (1 + 0.06)¹ = ₹ 1.06 - Year 4: The deposit of ₹ 1 will not earn any interest: A₀ = ₹ 1
Total Future Value: The aggregate future value at the end of the fourth year is:
- ₹ (1.191 + 1.124 + 1.060 + 1.00) = ₹ 4.375
This calculation represents the future value of an annuity of ₹ 1 for four years at a 6% interest rate.
Formula for Future Value of Annuity
The future value of an annuity can be expressed using the formula:
A(n, i) = A × n × (1 + i)ⁿ - 1 / i
- A: Periodic payments (e.g., ₹ 1)
- n: Number of periods (e.g., 4 years)
- i: Interest rate (e.g., 6% or 0.06)
Extended Formula for n Periods
The formula can be extended for n periods as:
A(n, i) = A × (1 + i)⁰ + A × (1 + i)¹ + ... + A × (1 + i)ⁿ⁻¹
- A = ₹ 1 (or any periodic payment)
- This formula represents a geometric series with a common ratio of (1 + i).
Future Value of Annuity Formula
The future value of an annuity can be calculated using the formula:
A(n, i) = A × n × (1 + i)ⁿ - 1 / i
- A: Periodic payments
- n: Number of periods
- i: Interest rate per period
Examples of Future Value of Annuity
Example 1: Future Value of an Annuity with Annual Payments
Find the future value of an annuity of ₹ 500 made annually for 7 years at an interest rate of 14% compounded annually. Given that (1.14)⁷ = 2.5023.
Solution:
A(7, 0.14) = 500 × 7 × (1 + 0.14)⁷ - 1 / (0.14)
- Annual Payment (A) = ₹ 500
- Number of Years (n) = 7
- Interest Rate (i) = 14% = 0.14
- Future Value of Annuity:
- = 500 × (2.5023 - 1) / 0.14
- = ₹ 5,365.35
Example 2: Future Value of a Monthly Annuity
If ₹ 200 is invested at the end of each month in an account paying 6% interest per year compounded monthly, what is the future value of this annuity after the 10th payment? Given that (1.005)¹⁰ = 1.0511.
Solution:
A(10, 0.005) = 200 × 10 × (1 + 0.005)¹⁰ - 1 / 0.005
- Monthly Payment (A) = ₹ 200
- Number of Months (n) = 10
- Monthly Interest Rate (i) = 6% per annum = 6/12% per month = 0.005
- Future Value of Annuity after 10 Months:
- = 200 × (1.0511 - 1) / 0.005
- = 200 × 10.22
- = ₹ 2,044
Future Value of Annuity Due or Annuity Immediate
In an Annuity Due or Annuity Immediate, the first payment or receipt occurs today. This differs from a regular annuity, where the first payment is made at the end of the first period. The relationship between the future value of an annuity due and an ordinary annuity is as follows:
Future Value of an Annuity Due/Annuity Immediate. Future Value of an Ordinary Annuity × (1 + i)
Here, i represents the interest rate in decimal form.
Calculating the Future Value of Annuity Due
To calculate the future value of an annuity due, follow these two steps:
Step 1: Calculate the future value as if it were an ordinary annuity.
Step 2: Multiply the result by (1 + i).
Example: Suppose Z invests ₹10,000 every year starting from today for the next 10 years, with an interest rate of 8% per annum compounded annually. We want to calculate the future value of this annuity. Given that (1 + 0.08)10 = 2.15892500.
Solution:
Step 1: Calculate Future Value as Ordinary Annuity
- Future Value of the annuity as if it is an ordinary annuity:
- = ₹10,000 × [ (1 + 0.08)10 - 1 ] / 0.08
- = ₹10,000 × 14.4865625
- = ₹1,44,865.625
Step 2: Multiply by (1 + i)
- = ₹1,44,865.625 × (1 + 0.08)
- = ₹1,56,454.875
Present Value
Present value refers to the current worth of a sum of money that will be received or paid in the future, discounted at a specific interest rate.
Present Value: The present value (PV) is calculated using the formula: PV = A n / (1 + i) n where:
A n = Future amount
i = Interest rate (as a decimal)
n = Number of periods
Example Calculation: For instance, to find the present value of ₹1 to be received after two years at a 10% interest rate, the calculation would be: PV = 1 / (1 + 0.1) 2 = 1 / 1.21 ≈ 0.8264 This means that ₹0.83 today will grow to ₹1 in two years at a 10% annual interest rate.
Present Value of Larger Sums: For larger sums, such as ₹10,000 to be received after 5 years at a 9% interest rate, the present value can be calculated as: PV = 10,000 / (1 + 0.09) 5 = 10,000 / 1.5386 ≈ 6,499.42 This indicates that ₹6,499.42 today is equivalent to ₹10,000 in 5 years at a 9% annual interest rate.
Given Data
- Annual Payment (PMT): ₹1,000
- Number of Payments (n): 5 years
- Interest Rate (r): 10% or 0.10
Present Value Formula:
The present value (PV) of an annuity can be calculated using the formula: PV = PMT × [(1 - (1 + r)^-n) / r]
Calculation Steps
- Calculate the annuity factor: PV factor = (1 - (1 + 0.10)^-5) / 0.10
- Calculate the present value: PV = ₹1,000 × PV factor
Detailed Calculation1. Calculate the PV factor:
- (1 + 0.10)-5 = 0.620921
- 1 - 0.620921 = 0.379079
- PV factor = 0.379079 / 0.10 = 3.79079
2. Calculate the present value:
PV = ₹1,000 × 3.79079 = ₹3,790.79
ConclusionThe present value of receiving ₹1,000 a
- Annual Payment (PMT): ₹1,000
- Number of Payments (n): 5 years
- Interest Rate (r): 10% or 0.10
Present Value Formula:
The present value (PV) of an annuity can be calculated using the formula: PV = PMT × [(1 - (1 + r)^-n) / r]
Calculation Steps
- Calculate the annuity factor: PV factor = (1 - (1 + 0.10)^-5) / 0.10
- Calculate the present value: PV = ₹1,000 × PV factor
Detailed Calculation1. Calculate the PV factor:
- (1 + 0.10)^-5 = 0.620921
- 1 - 0.620921 = 0.379079
- PV factor = 0.379079 / 0.10 = 3.79079
2. Calculate the present value:
PV = ₹1,000 × 3.79079 = ₹3,790.79
ConclusionThe present value of receiving ₹1,000 at the end of each year for 5 years at a 10% interest rate is approximately ₹3,790.79.
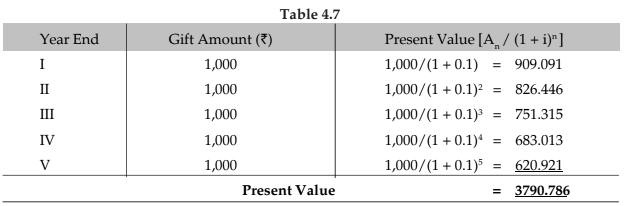
Thus the present value of annuity of ₹ 1,000 for 5 years at 10% is ₹ 3,790.79
It means if you want lump sum payment today instead of ₹ 1,000 every year you will get ₹ 3,790.79.
The above computation can be written in formula form as below.
The present value (V) of an annuity (A) is the sum of the present values of the payments.

We can extend above equation for n periods and rewrite as follows:
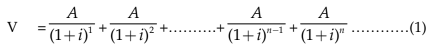
1 multiplying throughout by  we get
we get
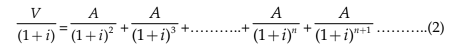
subtracting (2) from (1) we get

Consequently 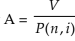 which is useful in problems of amortization.
which is useful in problems of amortization.
A loan with fixed rate of interest is said to be amortized if entire principal and interest are paid over equal periods of time by way of sequence of equal payment.
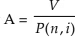 can be used to compute the amount of annuity if we have present value (V), n the P(n,i) number of time period and/the rate of interest in decimal.
can be used to compute the amount of annuity if we have present value (V), n the P(n,i) number of time period and/the rate of interest in decimal.
Examples on Present Value of Annuity
Example 32: Loan Repayment
A loan is being repaid with annual payments of ` 5,000 for ten years. If the interest rate is 14% per annum compounded annually, what is the original loan amount?
Solution:
- To find the loan amount (V), we use the formula: V = A × P(n, i) where: A. annual payment = ` 5,000 n. number of years = 10 i. interest rate = 0.14 (14%)
- P(n, i) is the present value factor, which can be found in tables or calculated using a formula. For this example, P(10, 0.14). 5.21611.
- Now, substituting the values: V = 5000 × P(10, 0.14)= 5000 × 5.21611≈ 26,080.55
Therefore, the loan amount is approximately ₹ 26,080.55.
Note: The value of P(10, 0.14) can be obtained from statistical tables or calculated using relevant formulas.
Example 33: TV Purchase Financing
Y purchased a TV for ₹ 13,000 by making an initial payment of ₹ 3,000 and agreeing to pay the remaining balance in equal annual installments over four years. If the interest rate on the unpaid amount is 14% compounded annually, what will be the amount of each annual payment?
Solution: In this scenario, the present value of the annuity is₹10,000 (calculated as ₹ 13,000 - ₹ 3,000 ). We need to determine the equal annual payment over a period of four years.
We use the formula: V = A × P(n, i) where: V. present value of the annuity A. annual payment P(n, i). present value factor n. number of years i. interest rate
- Rearranging the formula to find A. A = V / P(n, i)
- Substituting the values: A = 10,000 / P(4, 0.14)
- From tables, P(4, 0.14) ≈ 2.91371
- Now, calculating A: A ≈ 10,000 / 2.91371 ≈ 3,432.05
Therefore, each annual payment would be approximately ₹ 3,432.05.
Present Value of Annuity Due or Annuity Immediate
The present value of an annuity due or immediate for n years is equivalent to the present value of a regular annuity for (n-1) years plus an initial payment or receipt at the beginning of the period. To calculate the present value of an annuity due, follow these two steps:
- Step 1: Calculate the present value of the annuity as if it were a regular annuity for one period less.
- Step 2: Add the initial cash payment or receipt to the value obtained in Step 1.
Example 34: Suppose your mom decides to gift you ₹ 10,000 every year starting from today for the next five years. You deposit this amount in a bank as and when you receive and get 10% per annum interest rate compounded annually. What is the present value of this annuity?
Solution: It is an annuity immediate. For calculating value of the annuity immediate following steps will be followed:
Step 1: Present value of the annuity as if it were a regular annuity for one year less i.e. for four years
= ₹ 10,000 × P (4, 0.10)
= ₹ 10,000 × 3.16987
= ₹ 31,698.70
Step 2: Add initial cash deposit to the step 1 value
₹ (31,698.70+10,000) = ₹ 41,698.70
It is the fund credited for a specified purpose by way of sequence of periodic payments over a time period at a specified interest rate. Interest is compounded at the end of every period. Size of the sinking fund deposit is computed from A = P.A(n, i) where A is the amount to be saved, P the periodic payment, n the payment period.
Sinking Funds
It is the fund credited for a specified purpose by way of sequence of periodic payments over a time period at a specified interest rate. Interest is compounded at the end of every period. Size of the sinking fund deposit is computed from A = P.A(n, i) where A is the amount to be saved, P the periodic payment, n the payment period.Example 35: How much amount is required to be invested every year so as to accumulate ₹ 300000 at the end of 10 years if interest is compounded annually at 10%?
Solution: Here A = 3,00,000
n = 10
i = 0.1
Since A= PA (n, i)
300000 = P.A.(10, 0.1)
= P × 15.9374248
∴P = 3,00,000 / 15.9374248 = ₹ 18,823.62This value can also be calculated by the formula of future value of annuity regular. We know that
Applications
- Leasing is a financial agreement where the owner of an asset, known as the lessor, allows someone else, called the lessee, to use that asset for a specific period.
- The time period for which the asset can be used is referred to as the lease period.
- The lessee pays the lessor a fee, known as the lease rental, in exchange for using the asset during the lease period.
- This arrangement is similar to renting an asset.
- To determine if a lease agreement is beneficial for the lessor or the lessee, we can look at examples and specific terms involved in the lease.
Example 36: ABC Ltd. wants to lease out an asset costing ₹ 3,60,000 for a five year period. It has fixed a rental of ` 1,05,000 per annum payable annually starting from the end of first year. Suppose rate of interest is 14% per annum compounded annually on which money can be invested by the company. Is this agreement favourable to the company?
Solution: First we have to compute the present value of the annuity of ₹ 1,05,000 for five years at the interest rate of 14% p.a. compounded annually.
The present value V of the annuity is given by
V = A.P (n, i)
= 1,05,000 × P(5, 0.14)
= 1,05,000 × 3.43308 = ₹ 3,60,473.40
which is greater than the initial cost of the asset and consequently leasing is favourable to the lessor.
Example 37: A company is considering proposal of purchasing a machine either by making full payment of ₹ 4,000 or by leasing it for four years at an annual rate of ₹ 1,250. Which course of action is preferable if the company can borrow money at 14% compounded annually?
Solution: The present value V of annuity is given by
V = A.P (n, i)
= 1,250 × P (4, 0.14)
= 1,250 × 2.91371 = ₹ 3,642.11
which is less than the purchase price and consequently leasing is preferable.
Capital Expenditure (investment decision)
Capital expenditure means purchasing an asset (which results in outflows of money) today in anticipation of benefits (cash inflow) which would flow across the life of the investment. For taking investment decision we compare the present value of cash outflow and present value of cash inflows. If present value of cash inflows is greater than present value of cash outflows decision should be in the favour of investment. Let us see how do we take capital expenditure (investment) decision.Example 38: A machine can be purchased for ₹ 50000. Machine will contribute ₹ 12000 per year for the next five years. Assume borrowing cost is 10% per annum compounded annually. Determine whether machine should be purchased or not.
Solution: The present value of annual contribution
V = A.P(n, i)
= 12,000 × P(5, 0.10)
= 12,000 × 3.79079
= ₹ 45,489.48
which is less than the initial cost of the machine. Therefore machine must not be purchased.
Example 39: A machine with useful life of seven years costs ₹ 10,000 while another machine with useful life of five years costs ₹8,000. The first machine saves labour expenses of₹ 1,900 annually and the second one saves labour expenses of ₹ 2,200 annually. Determine the preferred course of action. Assume cost of borrowing as 10% compounded per annum.
Solution:
The present value of annual cost savings for the first machine
= ₹ 1,900 × P (7, 0.10)
= ₹ 1,900 × 4.86842
= ₹9,249.99
= ₹ 9,250
Cost of machine being ₹ 10,000 it costs more by ₹ 750 than it saves in terms of labour cost.
The present value of annual cost savings of the second machine
= ₹ 2,200 × P(5, 0.10)
= ₹ 2,200 × 3.79079
= ₹ 8,339.74
Cost of the second machine being₹ 8,000 effective savings in labour cost is ₹ 339.74. Hence the second machine is preferable.
Valuation of Bond
A bond is a debt security in which the issuer owes the holder a debt and is obliged to repay the principal and interest. Bonds are generally issued for a fixed term longer than one year.The bond issuer enters into contract with bondholder to pay interest.
Example 40: An investor intends purchasing a three year ₹ 1,000 par value bond having nominal interest rate of 10%. At what price the bond may be purchased now if it matures at par and the investor requires a rate of return of 14%?
Solution: Present value of the bond
Thus the purchase value of the bond is ₹ 907.125
Perpetuity
Perpetuity is an annuity in which the periodic payments or receipts begin on a fixed date and continue indefinitely or perpetually. Fixed coupon payments on permanently invested (irredeemable) sums of money are prime examples of perpetuities.
The formula for evaluating perpetuity is relatively straight forward. Two points which are important to understand in this regard are:.
(a) The value of the perpetuity is finite because receipts that are anticipated far in the future have extremely low present value (today’s value of the future cash flows).
(b) Additionally, because the principal is never repaid, there is no present value for the principal.
Therefore, the price of perpetuity is simply the coupon amount over the appropriate discount rate or yield.
Calculation of multi period perpetuity:
The formula for determining the present value of multi-period perpetuity is as follows:
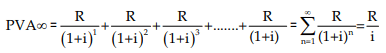 Where:
Where:
R = the payment or receipt each period
i = the interest rate per payment or receipt period
Example 41: Ramesh wants to retire and receive ₹ 3,000 a month. He wants to pass this monthly payment to future generations after his death. He can earn an interest of 8% compounded annually. How much will he need to set aside to achieve his perpetuity goal?
Solution:
R = ₹3,000
i = 0.08/12 or 0.00667
Substituting these values in the above formula, we get
PVA = ₹ 3,000 / 0.00667 = ₹ 4,49,775
If he wanted the payments to start today, he must increase the size of the funds to handle the first payment. This is achieved by depositing ₹ 4,52,775 (PV of normal perpetuity + perpetuity received in the beginning = 4,49,775 + 3,000) which provides the immediate payment of ₹ 3,000 and leaves ₹` 4,49,775 in the fund to provide the future ₹3,000 payments.
Calculation of Growing Perpetuity:
A stream of cash flows that grows at a constant rate forever is known as growing perpetuity.
The formula for determining the present value of growing perpetuity is as follows:
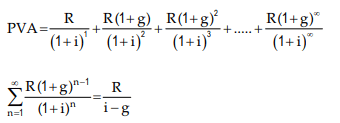
Example 42: Assuming that the discount rate is 7% per annum, how much would you pay to receive ₹ 50, growing at 5%, annually, forever?
Solution:
Where
R = Cash flow stream, i = interest rate or discount rate, g = growth rate in interest
Calculating Rate of Return:
(1) Calculating the rate of return provides important information that can be used for future investments. For example, if you invested in a stock that showed a substantial gain after several months of performance, you may decide to purchase more of that stock. If the stock showed a continual loss, it may be wise to conduct research to find a better-performing stock.
(2) Calculating the rate of return is that it allows you to gauge your investment and decision-making skills. Investments that create a gain or profit are great. However, if you continually make investments at a loss, then you may want to change your investment strategies. A great attribute of successful business people is knowing how and when to make investments, as is knowing when to change strategies. With a firm grasp of calculating the rate of return, you can manage and monitor your investments at various stages to determine the outcome of your investments. This leads to a higher level of confidence and the skills necessary to be a savvy investor.
Net Present Value Technique (NPV): The net present value technique is a discounted cash flow method that considers the time value of money in evaluating capital investments. An investment has cash flows throughout its life, and it is assumed that a rupee of cash flow in the early years of an investment is worth more than a rupee of cash flow in a later year.
The net present value method uses a specified discount rate to bring all subsequent net cash inflows after the initial investment to their present values (the time of the initial investment is year 0).
Determining Discount Rate
The discount rate, or desired rate of return, represents the return a firm could achieve by investing in the best alternative with equivalent risk. Since identifying the optimal alternative is challenging, organizations often use a different benchmark for the desired return. This benchmark may be a minimum rate that all capital projects must achieve, based on industry averages or other investment costs. Many firms utilize the Weighted Average Cost of Capital (WACC) that reflects the costs incurred or expected to be incurred when raising funds for investments. The net present value (NPV) of a project indicates the current value of the earnings from the investment after accounting for the cost of capital over time.
Net Present Value
Net present value = Present value of net cash inflow – Total net initial investmentSince it might be possible that some additional investment may also be required during the life time of the project then appropriate formula shall be:
Net present value = Present value of cash inflow – Present value of cash outflow
The steps to calculate net present value are:-
1. Determine the net cash inflow in each year of the investment.
2. Select the desired rate of return or discounting rate or Weighted Average Cost of Capital.
3. Find the discount factor for each year based on the desired rate of return selected.
4. Determine the present values of the net cash flows by multiplying the cash flows by respective the discount factors of respective period called Present Value (PV) of Cash flows
5. Total the amounts of all PVs of Cash Flows
Decision Rule:
- If NPV > 0 Accept the Proposal
- If NPV < 0
- Reject the Proposal
Example 43: Compute the net present value for a project with a net investment of ₹ 1,00,000 and net cash flows for year one is ` 55,000; for year two is ₹ 80,000 and for year three is ₹ 15,000. Further, the company’s cost of capital is 10%?
[PVIF @ 10% for three years are 0.909, 0.826 and 0.751]
Solution:
Recommendation: Since the net present value of the project is positive, the company should accept the project.
Nominal Rate of Return
- The nominal rate is the interest rate that is stated. For example, if a bank offers a 5% interest rate on a savings account each year, that 5% is the nominal interest rate.
- If you deposit `100 for one year, you will earn `5 in interest. However, at the end of the year, that Rs. 5 may not have the same value due to inflation, which reduces the purchasing power of money as prices for goods, services, and assets, like real estate, increase.
- The nominal interest rate is the simplest way to describe an interest rate. It is just the stated rate for a specific bond or loan and is based on simple interest, not accounting for any compounding periods.
- The real rate of return refers to the actual rate that a lender or investor gets after considering inflation. This means it is the interest rate that is higher than the inflation rate.
- To compare the real and nominal interest rates, you can use this formula:
- Nominal Rate of Return - Inflation = Real Rate of Return
- Nominal Interest Rate = Real Interest Rate + Inflation
Effective Rate:
It is the actual equivalent annual rate of interest at which an investment grows in value when interest is credited more often than once a year. If interest is paid m times in a year it can be found by calculating:
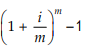
The chief advantage to knowing the difference between nominal, real and effective rates is that it allows consumers to make better decisions about their loans and investments. A loan with frequent compounding periods will be more expensive than one that compounds annually. A bond that only pays a 1% real interest rate may not be worth investors’ time if they seek to grow their assets over time. These rates effectively reveal the true return that will be posted by a fixed-income investment and the true cost of borrowing for an individual or business.
Effective and nominal interest rates allow banks to use the number that looks most advantageous to the consumer. When banks are charging interest, they advertise the nominal rate, which is lower and does not reflect how much interest the consumer would owe on the balance after a full year of compounding. On the other hand, with deposit accounts where banks are paying interest, they generally advertise the effective rate because it is higher than the nominal rate.
Compound Annual Growth Rate (CAGR)
Compound Annual Growth Rate (CAGR) is a business and investing specific term for the smoothed annualized gain of an investment over a given time periodit is not an accounting term, but remains widely used, particularly in growth industries or to compare the growth rates of two investments because CAGR dampens the effect of volatility of periodic returns that can render arithmetic means irrelevant. CAGR is often used to describe the growth over a period of time of some element of the business, for example revenue, units delivered, registered users, etc.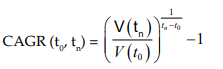
Where V(t0 ) = Beginning Period ; V( tn ) = End Period
Example: Suppose the revenues of a company for four years, V(t) in the above formula, have been

Calculate Compound annual Growth Rate.
Solution:
tn -t0 = 2016 - 2013 = 3
The CAGR revenues over the three-year period from the end of 2013 to the end of 20016 is
Applications: These are some of the common CAGR applications:
- Calculating average returns of investment funds.
- Demonstrating and comparing the performance of investment advisors.
- Comparing the historical returns of stocks with bonds or with a savings account.
- Forecasting future values based on the CAGR of a data series.
- Analyzing and communicating the behavior, over a series of years, of different business measures such as sales, market share, costs, customer satisfaction, and performance.
|
114 videos|164 docs|98 tests
|
FAQs on Mathematics of Finance Chapter Notes - Quantitative Aptitude for CA Foundation
| 1. What is the difference between simple interest and compound interest? |  |
| 2. How do lenders determine the interest rate for loans? |  |
| 3. What is the effective interest rate, and how is it different from the nominal interest rate? |  |
| 4. What is an annuity, and how does it relate to future and present value calculations? |  |
| 5. How do you calculate the future value of an investment or loan? |  |
|
114 videos|164 docs|98 tests
|

|
Explore Courses for CA Foundation exam
|

|






















