Rational and Irrational Numbers Chapter Notes | Mathematics Class 9 ICSE PDF Download
Introduction
Numbers are the building blocks of mathematics, and understanding their types opens up a fascinating world of patterns and logic. The chapter "Rational and Irrational Numbers" takes us on an exciting journey through the number system, where we explore how numbers can be categorised into real and imaginary, and further into rational and irrational. This exploration helps us understand why some numbers can be neatly expressed as fractions, while others, like the square root of a non-perfect square, surprise us with their infinite, non-repeating decimal expansions. By diving into this chapter, we’ll uncover the beauty of numbers and learn how to work with them in various mathematical operations, setting a strong foundation for more advanced concepts.
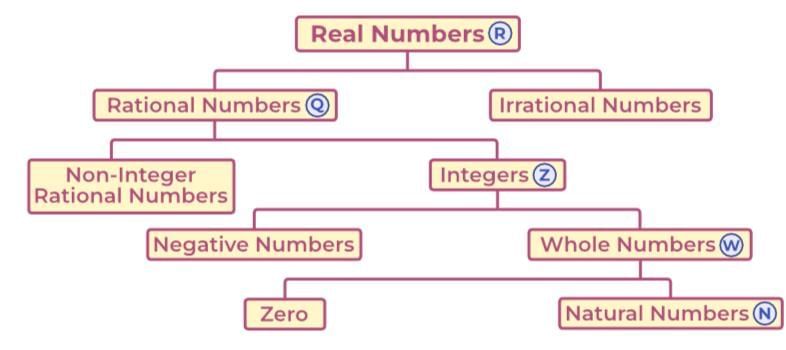
- The number system is divided into two main types: imaginary numbers and real numbers.
- Imaginary numbers arise from the square root of negative numbers, such as √(-4).
- Real numbers include all numbers that are not imaginary, like √4 = 2.
- This chapter focuses only on real numbers, which are further classified into rational and irrational numbers.
- Rational numbers can be expressed as fractions, while irrational numbers cannot.
Rational Numbers
- A rational number is expressed as a/b, where:
- b ≠ 0.
- a and b are integers with no common factors other than 1 (co-primes).
- b is usually positive, while a can be positive, negative, or zero.
- Every integer (positive, negative, or zero) and every decimal number (terminating or recurring) is a rational number.
- For every rational number a/b, its negative is -a/b, which equals a/(-b) or -(a/b).
- Two rational numbers a/b and c/d are equal if a × d = b × c.
- Comparison of rational numbers:
- a/b > c/d if a × d > b × c.
- a/b < c/d if a × d < b × c.
- The average of two rational numbers a and b, (a+b)/2, is a rational number lying between a and b.
- There are infinitely many rational numbers between any two rational numbers.
- For rational numbers a/b and c/d, (a+c)/(b+d) is a rational number lying between them.
- Since 3 < 5, find the average: (3+5)/2 = 4, so 3 < 4 < 5.
- Find averages again: (3+4)/2 = 7/2 = 3.5 and (4+5)/2 = 9/2 = 4.5.
- Thus, 3.5, 4, and 4.5 are three rational numbers between 3 and 5.
Method for Finding Rational Numbers Between Two Given Rational Numbers
To find n rational numbers between two rational numbers x and y (x < y):
- Calculate d = (y - x)/(n+1).
- The n rational numbers are: x + d, x + 2d, x + 3d, ..., x + nd.
- Since 2/3 < 5/6 (as 2 × 6 < 5 × 3), let x = 2/3, y = 5/6, n = 4.
- Calculate d = (5/6 - 2/3)/(4+1) = (5/6 - 4/6)/5 = (1/6)/5 = 1/30.
- Rational numbers are: 2/3 + 1/30 = 21/30 = 7/10, 2/3 + 2/30 = 22/30 = 11/15, 2/3 + 3/30 = 23/30, 2/3 + 4/30 = 24/30 = 4/5.
Alternative Method
- Find the LCM of the denominators of the given rational numbers.
- Convert both rational numbers to have the LCM as the denominator.
- Multiply the numerator and denominator of each by (n+1), where n is the number of rational numbers needed.
- Choose numbers with the new denominator and numerators between the converted numerators.
- LCM of denominators 3 and 6 is 6.
- Convert: 2/3 = 4/6, 5/6 = 5/6.
- Since n = 4, multiply by 4+1 = 5: 4/6 = 20/30, 5/6 = 25/30.
- Rational numbers between 20/30 and 25/30: 21/30 = 7/10, 22/30 = 11/15, 23/30, 24/30 = 4/5.
Properties of Rational Numbers (Q)
- The sum of two or more rational numbers is always a rational number.
- The difference of two rational numbers is always a rational number.
- The product of two or more rational numbers is always a rational number.
- The division of a rational number by a non-zero rational number is always a rational number.
- Rational numbers are closed under:
- Addition.
- Subtraction.
- Multiplication.
- Division (if divisor ≠ 0).
Decimal Representation of Rational Numbers
Rational numbers can be represented as:
- Terminating decimals (division ends with no remainder).
- Non-terminating recurring decimals (a digit or group of digits repeats).
Terminating decimals result from exact division, e.g., 1/8 = 0.125.
Non-terminating recurring decimals have a repeating digit or group, called the period.
Notation for recurring decimals:
- One repeating digit: Place a dot or bar over it, e.g., 0.333... = 0.3̅
- Two repeating digits: Place dots or bars over both, e.g., 0.295454... =
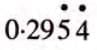
 to a rational number.
to a rational number.- Let x =
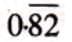 = 0.8282...
= 0.8282... - Since two digits repeat, multiply by 100: 100x = 82.8282...
- Subtract: 100x - x = 82.8282... - 0.8282... → 99x = 82 → x = 82/99.
Irrational Numbers
- Irrational numbers cannot be expressed as a/b, where a and b are integers and b ≠ 0.
- They are non-terminating, non-recurring decimals, e.g., √2, π.
- The product of a rational and an irrational number is irrational (if the rational number ≠ 0).
- The negative of an irrational number is irrational.
- The sum of a rational and an irrational number is irrational.
- The sum, difference, or product of two irrational numbers may or may not be irrational.
- √12 = √(2 × 2 × 3) = 2√3.
- Since 2 is rational and √3 is irrational, 2√3 is irrational.
- Thus, √12 is an irrational number.
Finding Irrational Numbers Between Two Numbers
For two positive numbers a and b (ab not a perfect square):
- Rational number between a and b: (a+b)/2.
- Irrational number between a and b: √(ab).
For irrational numbers √x and √y, √x > √y if x > y.
Comparing numbers with different roots requires making the indices the same.
- Since 2 × 3 = 6 is not a perfect square, one irrational number is √6.
- Between 2 and √6, another irrational number is √(2 × √6) = √(2√6).
- Thus, √6 and √(2√6) are two irrational numbers.
Alternative Method
- Express numbers as square roots, e.g., 2 = √4, 3 = √9.
- Choose numbers between 4 and 9 whose square roots are irrational, e.g., √5, √6.
Real Numbers (R)
- Real numbers are the union of rational (Q) and irrational (Q̅) numbers: R = Q ∪ Q̅.
- Rational numbers: Terminating or recurring decimals.
- Irrational numbers: Non-terminating, non-recurring decimals.
Surds (Radicals)
- A surd is a number of the form n√x, where x is a positive rational number, n is a positive integer, and n√x is irrational.
- Every surd is irrational, but not every irrational number is a surd (e.g., π is not a surd).
- The order of a surd n√x is n, where a is rational and n > 1.
- √27 = √(3 × 3 × 3) = 3√3, which is irrational.
- Since 27 is rational and √27 is irrational, √27 is a surd.
Rationalisation (For Surds of Order 2)
- Rationalisation is the process of multiplying a surd by its rationalising factor to make the product rational.
- Two surds are rationalising factors if their product is rational.
- The rationalising factor of a surd is not unique.
- √27 = 3√3.
- Multiply by √3: 3√3 × √3 = 3 × 3 = 9, which is rational.
- Thus, √3 is the least rationalising factor.
Simplifying an Expression by Rationalising Its Denominator
- To rationalise the denominator, multiply numerator and denominator by the rationalising factor of the denominator.
- For a denominator a + √b, the rationalising factor is a - √b (and vice versa).
- Simplify the resulting expression if necessary.
- Rewrite: 1/(√3 + √2 - 1) = 1/((√3 + √2) - 1).
- Rationalising factor: (√3 + √2) + 1.
- Multiply: [1 × (√3 + √2 + 1)]/[((√3 + √2) - 1)(√3 + √2 + 1)]
- = (√3 + √2 + 1)/(3 + 2 + 2√6 - 1) = (√3 + √2 + 1)/(4 + 2√6).
- Further rationalise: Multiply by (2 - √6)/(2 - √6) to get (√2 - 2 + √6)/4.
|
64 videos|136 docs|28 tests
|
FAQs on Rational and Irrational Numbers Chapter Notes - Mathematics Class 9 ICSE
| 1. What are rational numbers and how do they differ from irrational numbers? |  |
| 2. What are the properties of rational numbers? |  |
| 3. How can we represent rational numbers in decimal form? |  |
| 4. What are surds and how do you rationalise them? |  |
| 5. Why is it important to simplify expressions by rationalising the denominator? |  |
















