Rectilinear Figures Chapter Notes | Mathematics Class 9 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
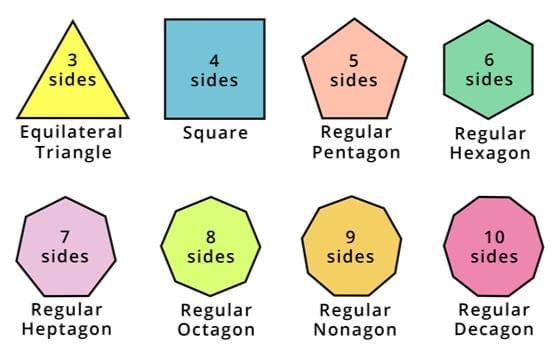
| Names of Polygons |

|
| Regular Polygon |

|
| Quadrilaterals |

|
| Special Kinds of Quadrilaterals |

|
| Diagonal Properties of Different Kinds of Parallelograms |

|
| Theorems |

|
Introduction
Embark on an exciting journey through the world of shapes and lines with the chapter on Rectilinear Figures! This chapter unveils the fascinating properties of polygons, especially quadrilaterals like parallelograms, rectangles, rhombuses, squares, and trapezoids. By exploring these straight-edged figures, you'll uncover the secrets of their angles, sides, and diagonals, making geometry both fun and understandable. Get ready to dive into a world where straight lines create captivating patterns and logical proofs!
- Rectilinear figures are shapes formed by straight lines.
- A plane figure enclosed by straight lines is called a rectilinear figure.
- A polygon is a closed shape with at least three straight sides.
- Example: A triangle is a rectilinear figure with three sides, and a quadrilateral has four sides.
Names of Polygons
Polygons are named based on their number of sides:
- Convex Polygon: All interior angles are less than 180°.
- Concave Polygon: At least one interior angle is greater than 180°.
- By default, a polygon is considered convex unless specified otherwise.
- The sum of the interior angles of a polygon with n sides = (2n - 4) × 90°.
- The sum of exterior angles of a polygon = 360° (or 4 right angles), regardless of the number of sides.
- Example: For a polygon with 12 sides:
Sum of interior angles = (2 × 12 - 4) × 90° = 20 × 90° = 1800°.
Given sum of interior angles = 5 × sum of exterior angles:
(2n - 4) × 90° = 5 × 360°
2n - 4 = 20
2n = 24
n = 12
So, the polygon has 12 sides.
Regular Polygon
- A regular polygon has all sides equal and all interior and exterior angles equal.
- Sum of interior angles of an n-sided polygon = (2n - 4) × 90°.
- Sum of exterior angles = 360°.
- At each vertex: Exterior angle + Interior angle = 180°.
- Each interior angle of a regular polygon = [(2n - 4) × 90°] / n.
- Each exterior angle of a regular polygon = 360° / n.
- If each exterior angle is x°, the number of sides = 360 / x.
- In a regular polygon, as the number of sides increases, each interior angle increases, and each exterior angle decreases.
- Example: If each interior angle of a regular polygon is 160°:
Each exterior angle = 180° - 160° = 20°.
Number of sides = 360° / 20° = 18.
For another polygon with sides = (2/3) × 18 = 12:
Each exterior angle = 360° / 12 = 30°.
Each interior angle = 180° - 30° = 150°.
Quadrilaterals
- A quadrilateral is a closed shape with four straight sides.
- It has four vertices and two diagonals (lines joining opposite vertices).
- Formula: Sum of the angles of a quadrilateral = 360°.
- Example: In a quadrilateral ABCD, the sum of angles A, B, C, and D is always 360°.
Special Kinds of Quadrilaterals
Trapezium
A trapezium has one pair of opposite sides parallel, and the other pair non-parallel.
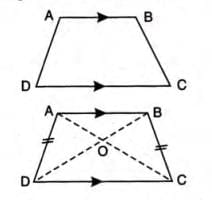 In an isosceles trapezium (non-parallel sides equal):
In an isosceles trapezium (non-parallel sides equal):
- Base angles are equal: ∠D = ∠C and ∠A = ∠B.
- Diagonals are equal: AC = BD.
- Diagonals intersect at a point O such that OA = OB and OC = OD.
Parallelogram
A parallelogram has both pairs of opposite sides parallel and equal.
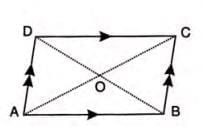 Properties:
Properties:
- Opposite sides are equal: AB = DC and AD = BC.
- Opposite angles are equal: ∠A = ∠C and ∠B = ∠D.
- Consecutive angles are supplementary: ∠A + ∠B = 180°, ∠B + ∠C = 180°, etc.
- Diagonals bisect each other: OA = OC and OB = OD.
- Each diagonal divides the parallelogram into two congruent triangles: △ABC ≅ △CDA and △ABD ≅ △CDB.
- Diagonals divide the parallelogram into four triangles of equal area.
Example: In parallelogram ABCD, if AB = 3x - 1 and DC = 2(x + 1):
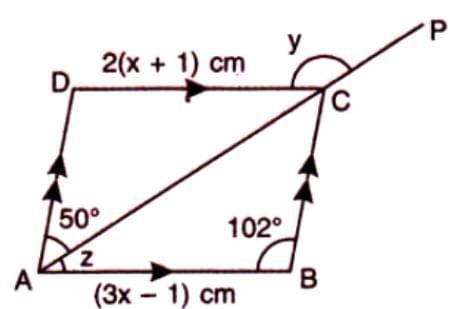 AB = DC
AB = DC
3x - 1 = 2(x + 1)
3x - 1 = 2x + 2
x = 3
Also, if ∠BCA = 50° and ∠ABC = 102°, then in △ABC:
z + ∠ABC + ∠BCA = 180°
z + 102° + 50° = 180°
z = 28°
Since AB // DC, ∠ACD = z = 28° (alternate angles).
On line ACP, ∠ACD + y = 180°
28° + y = 180°
y = 152°
Thus, x = 3, y = 152°, z = 28°.
Alternate Method:
∠DAB + ∠ABC = 180° (co-interior angles)
(50° + z) + 102° = 180°
z = 28°
Rectangle
A rectangle is a parallelogram with:
- Equal diagonals: AC = BD.
- Diagonals bisect each other: OA = OC and OB = OD.
- All angles equal to 90°.
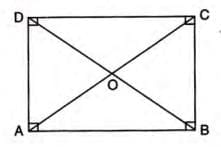
Example: In rectangle ABCD, diagonals AC and BD are equal, and each angle (∠A, ∠B, ∠C, ∠D) = 90°.
Rhombus
A rhombus is a parallelogram with all sides equal: AB = BC = CD = DA.
Properties:
- Diagonals bisect each other at 90°: ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°.
- Each diagonal bisects the angles at the vertices: AC bisects ∠A and ∠C; BD bisects ∠B and ∠D.
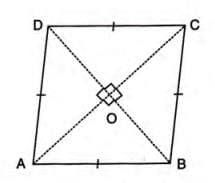
Example: In rhombus ABCD, if AB = 3x + 2 and AD = 4x - 4:
AB = AD
3x + 2 = 4x - 4
x = 6
If ∠DAB = 60°, then ∠ABC = 180° - 60° = 120° (co-interior angles).
Diagonal BD bisects ∠ABC: ∠ABD = 120° / 2 = 60°.
In △ABD, ∠DAB = ∠ABD = 60°, so third angle ∠ADB = 60°.
Thus, △ABD is equilateral, so BD = AB = 3x + 2 = 3 × 6 + 2 = 20.
If BD = y - 1, then y - 1 = 20, so y = 21.
Thus, x = 6, y = 21.
Square
A square is a parallelogram with:
- All sides equal.
- All angles equal to 90°.
- Equal diagonals.
- Diagonals bisect each other at 90°.
- Each diagonal bisects the angles at the vertices.
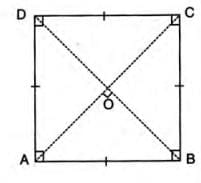
Example: In square ABCD, diagonals AC and BD are equal, and ∠AOB = 90°.
Diagonal Properties of Different Kinds of Parallelograms

Theorems
Theorem 11: Opposite Sides of a Parallelogram
Statement: In a parallelogram, both pairs of opposite sides are equal.
Proof Steps:
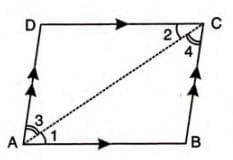
- Consider parallelogram ABCD, join diagonal AC.
- In △ABC and △CDA:
- ∠1 = ∠2 (alternate angles, AC cuts parallel sides AB and DC).
- ∠3 = ∠4 (alternate angles, AC cuts parallel sides AD and BC).
- AC = AC (common).
- △ABC ≅ △CDA (by ASA).
- AB = DC and AD = BC (by CPCTC).
Example: In parallelogram ABCD, if AB = DC and AD = BC, the proof confirms opposite sides are equal.
Theorem 12: Opposite Angles of a Parallelogram
Statement: In a parallelogram, both pairs of opposite angles are equal.
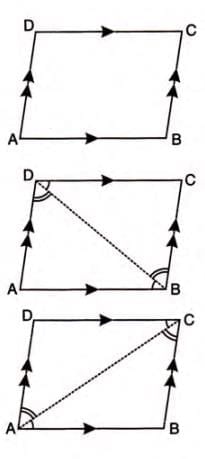 Proof Steps:
Proof Steps:
- Consider parallelogram ABCD, draw diagonal BD.
- Show △ABD ≅ △CDB, so ∠A = ∠C.
- Draw diagonal AC, show △ABC ≅ △CDA, so ∠B = ∠D.
- Thus, ∠A = ∠C and ∠B = ∠D.
Example: In parallelogram ABCD, opposite angles ∠A = ∠C and ∠B = ∠D are equal.
Theorem 13: Condition for a Parallelogram
Statement: If one pair of opposite sides of a quadrilateral is equal and parallel, it is a parallelogram.
Proof Steps:

- Consider quadrilateral ABCD with AB = DC and AB // DC, join AC.
- In △ABC and △CDA:
- ∠1 = ∠2 (alternate angles, AC cuts parallel sides AB and DC).
- AB = DC (given).
- AC = AC (common).
- △ABC ≅ △CDA (by SAS).
- ∠3 = ∠4 (by CPCTC).
- ∠3 and ∠4 are alternate angles, so AD // BC.
- Thus, ABCD is a parallelogram (opposite sides parallel).
Example: In quadrilateral ABCD, if AB = DC and AB // DC, it is a parallelogram.
Theorem 14: Diagonals Bisect a Parallelogram
Statement: Each diagonal of a parallelogram bisects the parallelogram into two congruent triangles.
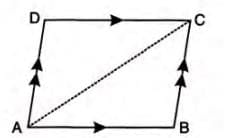 Proof Steps:
Proof Steps:
- Consider parallelogram ABCD, prove △ABC ≅ △CDA as in Theorem 11.
- Thus, △ABC = △CDA = 1/2 (area of parallelogram ABCD).
- Similarly, diagonal BD bisects the parallelogram.
Example: In parallelogram ABCD, diagonal AC divides it into △ABC and △CDA of equal area.
Theorem 15: Diagonals Bisect Each Other
Statement: The diagonals of a parallelogram bisect each other.
Proof Steps:
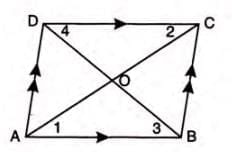
- Consider parallelogram ABCD with diagonals AC and BD intersecting at O.
- In △AOB and △COD:
- AB = DC (opposite sides of a parallelogram).
- ∠1 = ∠2 (alternate angles).
- ∠3 = ∠4 (alternate angles).
- △AOB ≅ △COD (by ASA).
- OA = OC and OB = OD (by CPCTC).
Example: In parallelogram ABCD, diagonals AC and BD intersect at O such that OA = OC and OB = OD.
Theorem 16: Diagonals of a Rhombus
Statement: The diagonals of a rhombus meet at right angles.
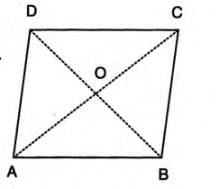 Proof Steps:
Proof Steps:
- Consider rhombus ABCD with diagonals AC and BD intersecting at O.
- AB = BC (sides of a rhombus are equal).
- OA = OC and OB = OD (diagonals of a parallelogram bisect each other).
- In △AOB and △COB:
- AB = CB, OA = OC, OB = OB.
- △AOB ≅ △COB (by SSS).
- ∠AOB = ∠BOC (by CPCTC).
- ∠AOB + ∠BOC = 180° (straight line).
- Thus, ∠AOB = ∠BOC = 90°.
Example: In rhombus ABCD, diagonals AC and BD intersect at 90°.
Theorem 17: Diagonals of a Rectangle
Statement: The diagonals of a rectangle are equal.
 Proof Steps:
Proof Steps:
- Consider rectangle ABCD with diagonals AC and BD.
- In △DAB and △CBA:
- AD = BC (opposite sides of a rectangle).
- AB = AB (common).
- ∠DAB = ∠CBA (each 90°).
- △DAB ≅ △CBA (by SAS).
- AC = BD (by CPCTC).
Example: In rectangle ABCD, diagonals AC = BD.
Theorem 18: Diagonals of a Square
Statement: The diagonals of a square are equal and meet at right angles.
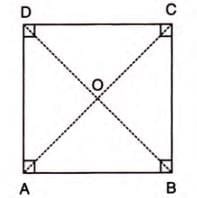 Proof Steps:
Proof Steps:
- Consider square ABCD with diagonals AC and BD intersecting at O.
- In △DAB and △CBA:
- AD = BC (sides of a square).
- ∠DAB = ∠CBA (each 90°).
- AB = AB (common).
- △DAB ≅ △CBA (by SAS).
- AC = BD (by CPCTC).
- In △AOB and △BOC:
- AB = BC, OA = OC, OB = OB.
- △AOB ≅ △BOC (by SSS).
- ∠AOB = ∠BOC, and ∠AOB + ∠BOC = 180°.
- Thus, ∠AOB = ∠BOC = 90°.
Example: In square ABCD, diagonals AC = BD and intersect at O with ∠AOB = 90°.
Solved example 1:
- Statement: The diagonals of a rhombus bisect the angles at the vertices they join.
- Proof Steps:
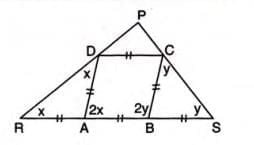
- Consider rhombus ABCD with diagonals AC and BD intersecting at point P.
- Since ABCD is a rhombus, AB = BS = BC = CD = DA (all sides are equal).
- Label angles: ∠DAR = ∠ADR = x (since RD is produced), and ∠ABC = ∠SBC = y.
- In △ABC, ∠ABC = y, so exterior ∠SBC = y, making ∠ABC = 2y (total angle at B).
- Since ABCD is a parallelogram, ∠DAB + ∠ABC = 180° (co-interior angles).
- So, 2x + 2y = 180°, hence x + y = 90°.
- In △RPS, ∠R + x + y = 180° (sum of angles in a triangle).
- Since x + y = 90°, ∠R = 180° - 90° = 90°.
- Thus, ∠R = ∠P = 90°, proving RD and SC meet at right angles when produced.
- Example: In rhombus ABCD, RABS is a straight line such that RA = AB = BS. Prove that RD and SC, when produced, meet at right angles (∠P = 90°). The proof above shows this using the properties of a rhombus and angle relationships.
Solved example 2:
- Statement:In a parallelogram, if a line from the midpoint of one side bisects an angle, then:
- BC = BE (side opposite the bisected angle equals the segment from the midpoint).
- CE bisects ∠C.
- ∠DEC = 90°.
- Proof Steps:
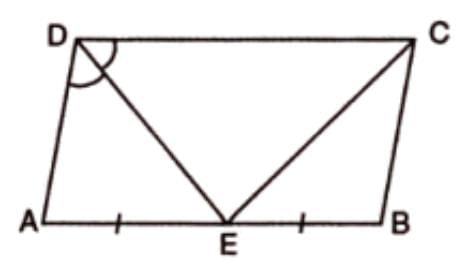
- Consider parallelogram ABCD, where E is the midpoint of AB, and DE bisects ∠D.
- Prove BC = BE:
- Since DE bisects ∠D, ∠CDE = ∠EDA (given).
- Also, ∠CDE = ∠DEA (alternate angles, since AB // DC).
- So, ∠DEA = ∠EDA (from above).
- In △DEA, since ∠DEA = ∠EDA, AD = AE (sides opposite equal angles).
- Since ABCD is a parallelogram, AD = BC (opposite sides).
- Also, AE = BE (E is midpoint of AB).
- Thus, BC = AD = AE = BE, so BC = BE.
- Prove CE bisects ∠C:
- Since BC = BE (from above), ∠BEC = ∠BCE (angles opposite equal sides in △BCE).
- Also, ∠BEC = ∠BCD (alternate angles, AB // DC).
- So, ∠BCE = ∠BCD, meaning CE bisects ∠BCD (i.e., ∠C).
- Prove ∠DEC = 90°:
- Since CE bisects ∠C, ∠DCE = 1/2 ∠BCD.
- Since DE bisects ∠D, ∠CDE = 1/2 ∠ADC.
- In △DEC, ∠DCE + ∠CDE + ∠DEC = 180° (sum of angles in a triangle).
- Since ∠BCD + ∠ADC = 180° (co-interior angles in parallelogram), 1/2 ∠BCD + 1/2 ∠ADC = 90°.
- Thus, ∠DCE + ∠CDE = 90°, so ∠DEC = 180° - 90° = 90°.
Solved example 3:
- Statement:In trapezium ABCD with AB // DC and AD = BC, prove:
- ∠A = ∠B (base angles are equal).
- ∠C = ∠D (base angles are equal).
- △ABC ≅ △BAD (triangles formed by diagonals are congruent).
- Diagonal AC = diagonal BD.
- Proof Steps:
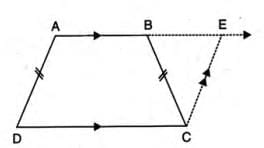
- Consider trapezium ABCD with AB // DC and AD = BC (isosceles trapezium).
- Draw CE parallel to DA, intersecting AB produced at point E.
- Prove ABCD is a parallelogram (temporary assumption):
- Since AB // DC (given) and CE // DA (by construction), ABCD is a parallelogram.
- So, AD = BC (given) and CE = AB (opposite sides of parallelogram).
- Prove ∠A = ∠B:
- In △ABE, AB = CE (from above) and AE = BE (since ABCE is a parallelogram).
- So, ∠ABE = ∠AEB (angles opposite equal sides).
- Since ∠ABE = ∠EBC (vertical angles), ∠ABC = ∠BCE (total angle at B).
- Also, ∠ABC = ∠EBC and ∠BCE = ∠BCD (alternate angles, AB // DC).
- Thus, ∠ABC = ∠BCD, so ∠ABC = ∠A (since ∠BCD = ∠A, co-interior angles).
- Prove ∠C = ∠D:
- Since ∠ABC = ∠A, we have ∠A + ∠D = 180° and ∠B + ∠C = 180° (co-interior angles).
- Since ∠A = ∠B, ∠C = ∠D (remaining angles).
- Prove △ABC ≅ △BAD:
- In △ABC and △BAD:
- AB = BA (common).
- BC = AD (given).
- ∠ABC = ∠BAD (proven above).
- So, △ABC ≅ △BAD (by SAS).
- Prove diagonal AC = diagonal BD:
- Since △ABC ≅ △BAD, AC = BD (corresponding sides of congruent triangles).
|
64 videos|136 docs|28 tests
|
FAQs on Rectilinear Figures Chapter Notes - Mathematics Class 9 ICSE
| 1. What are the characteristics of regular polygons? |  |
| 2. What are the different types of quadrilaterals and their properties? |  |
| 3. What are the special kinds of quadrilaterals and how do they differ from general quadrilaterals? |  |
| 4. What are the diagonal properties of different kinds of parallelograms? |  |
| 5. What theorems are important for understanding rectilinear figures in geometry? |  |














