Representing 3-D in 2-D Chapter Notes | Mathematics Class 8 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Polyhedron |

|
| Faces, Edges, and Vertices |

|
| Euler's Formula |

|
| More Polyhedrons (Polyhedra) |

|
| Net of a Solid |

|
Introduction
This chapter introduces students to the visualisation of two-dimensional (2-D) cross-sections of three-dimensional (3-D) objects. It focuses on helping students understand how 3-D shapes, like cubes, pyramids, and prisms, can be represented in 2-D. The chapter explores concepts like polyhedrons, their faces, edges, and vertices, Euler's formula, and nets of solids. By learning these concepts, students will develop skills to recognize and draw 2-D representations of 3-D objects, which is useful for understanding their structure and calculating properties like surface area.
Objectives
- Learn to visualise 2-D cross-sections of 3-D objects.
- Understand how 3-D shapes can be shown as 2-D diagrams.
- Focus on recognising and drawing 2-D cross-sections along a plane of a 3-D object.
- Explore different 3-D shapes like cubes, pyramids, and prisms through their 2-D representations.
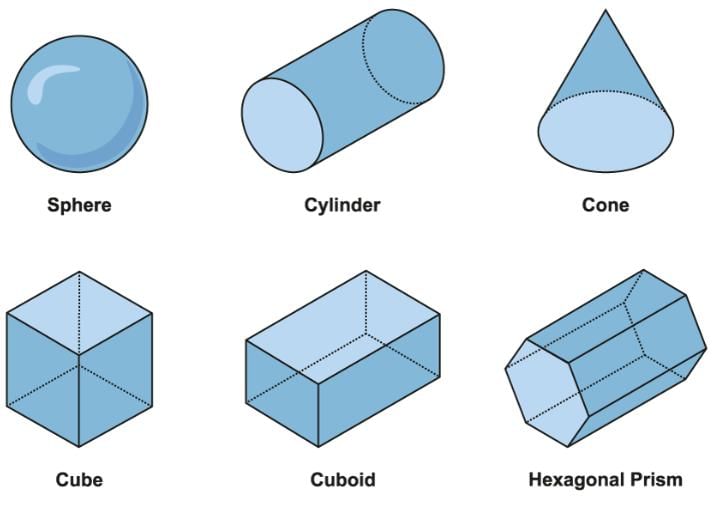
Polyhedron
- A polyhedron is a 3-D shape with flat faces and straight edges.
- Spheres, cylinders, and cones are not polyhedrons because they have curved surfaces, not flat polygonal regions.
- Polyhedra is the plural form of polyhedron.
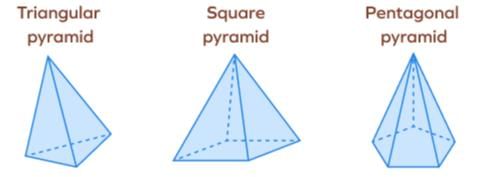
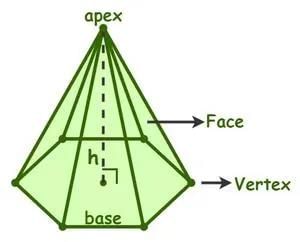
- Pyramids:
- A pyramid is a polyhedron with a polygon base and triangular lateral surfaces.
- In a right pyramid, the apex (top vertex) is directly above the center of the base, and the lateral surfaces are congruent triangles.
- Pyramids are named based on the shape of their base, e.g., a triangular pyramid has a triangle base.
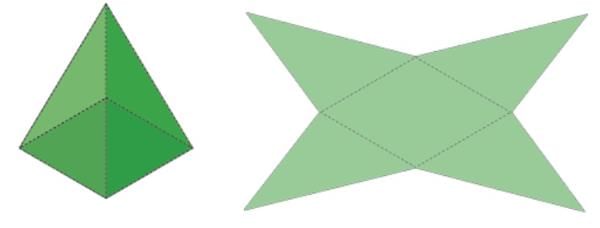
- A triangular pyramid is also called a tetrahedron, which has four triangular faces.
- A regular tetrahedron has equilateral triangle faces, with all sides equal and angles of 60°.
- Example:A tetrahedron has a triangular base and three triangular lateral faces, making a total of four faces, all equilateral triangles in a regular tetrahedron.
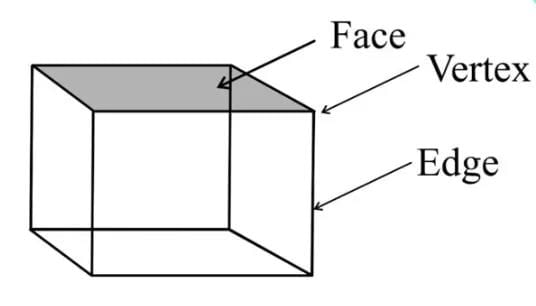
Faces, Edges, and Vertices
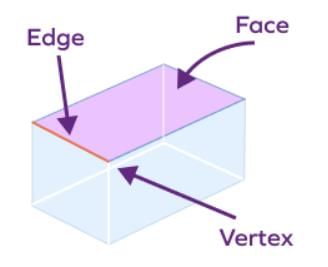
Faces (F):
- Faces are the flat polygonal surfaces that form a polyhedron.
- Each face is a polygon, like a triangle or square.
- Edges (E):
- Edges are the line segments where two faces of a polyhedron meet.
- Vertices (V):
- Vertices are the points where edges of a polyhedron intersect.
Example: A pyramid with a square base has five faces: one square base (ABCD) and four triangular faces (OAD, OBC, OAB, OCD). It has eight edges (OA, OB, OC, OD, AB, BC, CD, DA) and five vertices (O, A, B, C, D).
Euler's Formula
- Euler's formula applies to polyhedrons, which are closed 3-D shapes with flat faces and straight edges.
- The formula is: F + V - E = 2, where:
- F = Number of faces
- V = Number of vertices
- E = Number of edges
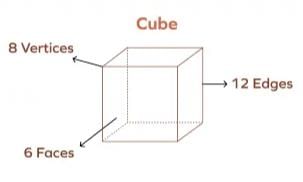
- This formula helps verify if a given set of faces, vertices, and edges forms a valid polyhedron.
- Example:For a pyramid with 5 faces (F = 5), 5 vertices (V = 5), and 8 edges (E = 8): F + V - E = 5 + 5 - 8 = 2. This satisfies Euler's formula, confirming it is a valid polyhedron.
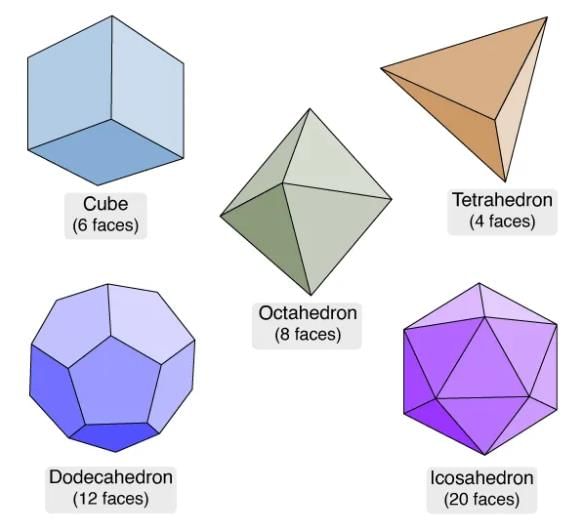
More Polyhedrons (Polyhedra)
- Cube:
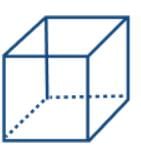
- A cube has 6 faces (all squares), 8 vertices, and 12 edges.
- Euler's formula: F + V - E = 6 + 8 - 12 = 2.
- Example:A cube has 6 square faces, 8 vertices, and 12 edges. Applying Euler's formula: 6 + 8 - 12 = 2, which is valid.
- Cuboid:
- A cuboid has 6 faces (all rectangles), 8 vertices, and 12 edges.
- Euler's formula: F + V - E = 6 + 8 - 12 = 2.
- Example:A cuboid has 6 rectangular faces, 8 vertices, and 12 edges. Applying Euler's formula: 6 + 8 - 12 = 2, which is valid.
- Triangular Prism:

- A triangular prism has 5 faces (2 triangles, 3 rectangles), 6 vertices, and 9 edges.
- Euler's formula: F + V - E = 5 + 6 - 9 = 2.
- Example:A triangular prism has 5 faces, 6 vertices, and 9 edges. Applying Euler's formula: 5 + 6 - 9 = 2, which is valid.
- Pentagonal Prism:

- A pentagonal prism has 7 faces (2 pentagons, 5 rectangles), 10 vertices, and 15 edges.
- Euler's formula: F + V - E = 7 + 10 - 15 = 2.
- Example:A pentagonal prism has 7 faces, 10 vertices, and 15 edges. Applying Euler's formula: 7 + 10 - 15 = 2, which is valid.
- Hexagonal Prism:
- A hexagonal prism has 8 faces (2 hexagons, 6 rectangles), 12 vertices, and 18 edges.
- Euler's formula: F + V - E = 8 + 12 - 18 = 2.
- Example:A hexagonal prism has 8 faces, 12 vertices, and 18 edges. Applying Euler's formula: 8 + 12 - 18 = 2, which is valid.
- Tetrahedron (Triangular Pyramid):

- A tetrahedron has 4 faces (all triangles), 4 vertices, and 6 edges.
- Euler's formula: F + V - E = 4 + 4 - 6 = 2.
- Example:A tetrahedron has 4 triangular faces, 4 vertices, and 6 edges. Applying Euler's formula: 4 + 4 - 6 = 2, which is valid.
- Rectangular Pyramid:
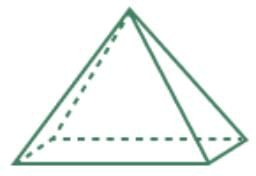
- A rectangular pyramid has 5 faces (1 rectangle, 4 triangles), 5 vertices, and 8 edges.
- Euler's formula: F + V - E = 5 + 5 - 8 = 2.
- Example:A rectangular pyramid has 5 faces, 5 vertices, and 8 edges. Applying Euler's formula: 5 + 5 - 8 = 2, which is valid.
- Square Pyramid:
- A square pyramid has 5 faces (1 square, 4 triangles), 5 vertices, and 8 edges.
- Euler's formula: F + V - E = 5 + 5 - 8 = 2.
- Example:A square pyramid has 5 faces, 5 vertices, and 8 edges. Applying Euler's formula: 5 + 5 - 8 = 2, which is valid.
- Pentagonal Pyramid:

- A pentagonal pyramid has 6 faces (1 pentagon, 5 triangles), 6 vertices, and 10 edges.
- Euler's formula: F + V - E = 6 + 6 - 10 = 2.
- Example:A pentagonal pyramid has 6 faces, 6 vertices, and 10 edges. Applying Euler's formula: 6 + 6 - 10 = 2, which is valid.
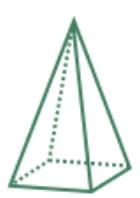
- Hexagonal Pyramid:
- A hexagonal pyramid has 7 faces (1 hexagon, 6 triangles), 7 vertices, and 12 edges.
- Euler's formula: F + V - E = 7 + 7 - 12 = 2.
- Example:A hexagonal pyramid has 7 faces, 7 vertices, and 12 edges. Applying Euler's formula: 7 + 7 - 12 = 2, which is valid.
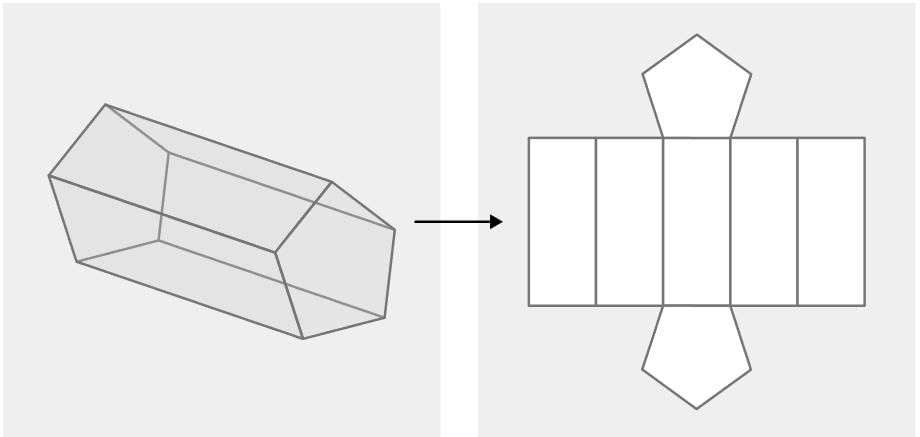
Net of a Solid
- A net is a 2-D shape that can be folded to form a 3-D solid.
- It shows all the faces of the solid laid out flat.
- A solid may have multiple possible nets.
- Steps to verify a net:
- Ensure the net has the same number of faces as the solid.
- Check that the shapes of the faces in the net match the solid’s faces.
- Visualise folding the net to ensure all sides fit together correctly.
- Nets are useful for finding the surface area of solids.
- Nets of a Cube:
- A cube has 11 possible nets, each with 6 square faces arranged differently.

- Example:A cube’s net consists of 6 squares arranged in a cross pattern or other configurations. When folded, these squares form the cube with all sides fitting together.
- Net of a Triangular Prism:
- Consists of 2 triangles and 3 rectangles.

- Example:A triangular prism’s net has 2 triangular faces and 3 rectangular faces, which can be folded to form the prism.
- Net of a Rectangular Pyramid:
- Consists of 1 rectangle and 4 triangles.
- Example:A rectangular pyramid’s net has 1 rectangular base and 4 triangular faces, which fold to form the pyramid.
- Net of a Cylinder:
- Consists of 2 circles and 1 curved rectangle.
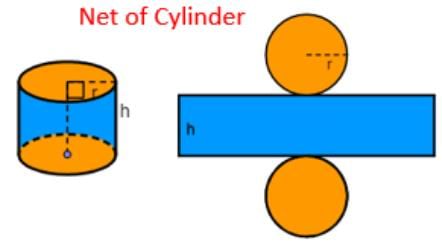
- Example:A cylinder’s net has 2 circular bases and 1 curved rectangular surface, which wraps around to form the cylinder.
- More Nets:
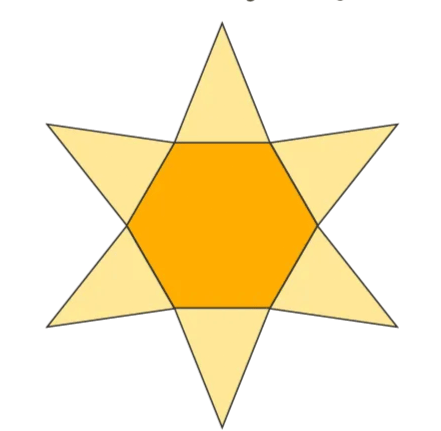
- Hexagonal Pyramid: 1 hexagon and 6 triangles.
- Tetrahedron: 4 triangles.

- Example:A square pyramid’s net has 1 square base and 4 triangular faces, which can be folded to form the pyramid.
|
23 videos|98 docs|14 tests
|
FAQs on Representing 3-D in 2-D Chapter Notes - Mathematics Class 8 ICSE
| 1. What is a polyhedron? |  |
| 2. How do you count the faces, edges, and vertices of a polyhedron? |  |
| 3. What is Euler's Formula and how is it applied to polyhedrons? |  |
| 4. What are some examples of different types of polyhedrons? |  |
| 5. What is a net of a solid and how is it used in geometry? |  |















