Sets, Relations and Functions Chapter Notes | Quantitative Aptitude for CA Foundation PDF Download
Chapter Overview

Definition of Sets
A set is a collection of distinct objects, considered as an object in its own right. The objects in a set are called the elements or members of the set.
Example. The set of all even numbers is a set. The elements of this set are all the even numbers, such as 2, 4, 6, 8, and so on.
Sets are usually denoted by capital letters, and their elements are denoted by lowercase letters. For example, the set of all even numbers can be denoted by E, and its elements can be denoted by e.
Example. A = {a, e, i, o, u} B = {2, 4, 6, 8, 10} C = {pqr, prq, qrp, rqp, qpr, rpq} D = {1, 3, 5, 7, 9} E = {1, 2}
Types of Sets
(a) Finite Set:. set is said to be finite if it contains a definite number of elements. For example, the set of all natural numbers less than 10 is a finite set, as it contains only 10 elements.
(b) Infinite Set:. set is said to be infinite if it contains an infinite number of elements. For example, the set of all natural numbers is an infinite set, as it contains an infinite number of elements.
(c) Equal Set: Two sets are said to be equal if they contain the same elements. For example, the set of all even numbers less than 10 and the set of all even numbers less than 10 are equal sets, as they contain the same elements.
(d) Subset:. set is said to be a subset of another set if all its elements are also elements of the other set. For example, the set of all even numbers less than 10 is a subset of the set of all even numbers, as all its elements are also elements of the set of all even numbers.
(e) Proper Subset:. set is said to be a proper subset of another set if it is a subset of the other set and its elements are not all elements of the other set. For example, the set of all even numbers less than 10 is a proper subset of the set of all even numbers, as it is a subset of the set of all even numbers but its elements are not all elements of the set of all even numbers.
(f) Universal Set: The set that contains all the elements of a particular problem is called the universal set. For example, the set of all natural numbers is a universal set, as it contains all the natural numbers.
(g) Singleton Set:. set that contains only one element is called a singleton set. For example, the set of all even numbers less than 10 is a singleton set, as it contains only one element.
(h) Empty Set or Null Set:. set that contains no elements is called an empty set or null set. For example, the set of all natural numbers less than 0 is an empty set, as it contains no elements.
(i) Power Set: The set of all subsets of a set is called the power set of the set. For example, the set of all subsets of the set of all even numbers less than 10 is called the power set of the set of all even numbers less than 10.
Representation of Sets
(i) Roster or Tabular Form: In this form, we list all the elements of the set within braces. For example, the set of all even numbers less than 10 can be represented as {2, 4, 6, 8}.
(ii) Set-Builder Form: In this form, we specify the property that the elements of the set satisfy. For example, the set of all even numbers less than 10 can be represented as {x : x is an even number and x < 10}.
Properties of Sets
(i) Commutative Property: The order of the elements in a set does not affect its properties. For example, the set {2, 4, 6} is the same as the set {6, 4, 2}.
(ii) Associative Property: The grouping of the elements in a set does not affect its properties. For example, the set {2, 4, 6} is the same as the set {2, 6, 4}.
(iii) Distributive Property: The distributive property states that the intersection of a set with the union of two other sets is the same as the union of the intersections of the set with each of the other sets. For example, A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
(iv) Idempotent Law: The idempotent law states that the union of a set with itself is the same as the set. For example, A ∪ A = A.
(v) Complement Law: The complement law states that the union of a set with its complement is the universal set. For example, A ∪ A' = U.
Operation on Sets
(i) Union of Sets: The union of two sets, A and B, is the set of all elements that are in either A or B or both. It is denoted by A ∪ B. For example, if A = {1, 2, 3} and B = {3, 4, 5}, then A ∪ B = {1, 2, 3, 4, 5}.
(ii) Intersection of Sets: The intersection of two sets, A and B, is the set of all elements that are in both A and B. It is denoted by A ∩ B. For example, if A = {1, 2, 3} and B = {3, 4, 5}, then A ∩ B = {3}.
(iii) Difference of Sets: The difference of two sets, A and B, is the set of all elements that are in A but not in B. It is denoted by A - B. For example, if A = {1, 2, 3} and B = {3, 4, 5}, then A - B = {1, 2}.
(iv) Complement of a Set: The complement of a set A is the set of all elements that are not in A. It is denoted by A'. For example, if A = {1, 2, 3} and the universal set U = {1, 2, 3, 4, 5}, then A' = {4, 5}.
Singleton Set: A set that has only one element is called a Singleton Set.
- For example, {1} is a singleton set where the only element is 1.
Equal Set: Two sets, A and B, are considered equal, written as A = B, if every element in A is also in B and vice versa.
- For example, if A = {2, 4, 6} and B = {2, 4, 6}, then we can say A = B.
Remarks:
- (I) The order of elements in two sets does not matter. Thus, {1, 2, 3} = {2, 1, 3} = {3, 2, 1}, etc.
- (II) Repeating elements in a set does not change its meaning. For instance, {x : x is a letter in the word "follow"} equals {f, o, l, w}.
Different Sets:
- Consider ∅, {0}, and 0 as different.
- ∅ is a set with no elements.
- {0} is a set with one element, which is 0.
- 0 itself is a number, not a set.
Universal Set: The set that includes all elements relevant to a specific problem is called the universal set, denoted by S.
- If P is a subset of S, then the complement of P, written as Pc (or P'), contains all elements in S that are not in P.
- This can also be represented as S - P or S ~ P.
- The formula can be expressed as S - P = {x : x ∈ S, x ∉ P}.
Examples:
- Let S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
- Let P = {0, 2, 4, 6, 8}
- Let Q = {1, 2, 3, 4, 5}
- Then:
- P' = {1, 3, 5, 7, 9}
- Q' = {0, 6, 7, 8, 9}
Set Operations:
- P ∪ Q = {0, 1, 2, 3, 4, 5, 6, 8}
- P ∩ Q = {2, 4}
- P ∪ Q' = {0, 2, 4, 6, 7, 8, 9}
- (P ∩ Q)' = {0, 1, 3, 5, 6, 7, 8, 9}
- P' ∪ Q' = {0, 1, 3, 5, 6, 7, 8, 9}
- P' ∩ Q' = {7, 9}
De Morgan's Laws:
- It can be observed that (P ∪ Q)' = P' ∩ Q' and (P ∩ Q)' = P' ∪ Q'.
Venn Diagrams
We may represent the above operations on sets by means of Euler - Venn diagrams.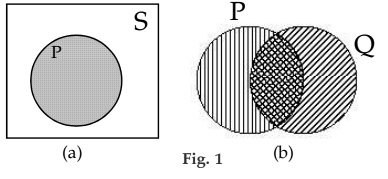
Thus Fig. 1(a) shows a universal set S represented by a rectangular region and one of its subsets P represented by a circular shaded region.
The un-shaded region inside the rectangle represents P'.
Figure 1(b) shows two sets P and Q represented by two intersecting circular regions. The total shaded area represents PUQ, the cross-hatched "intersection" represents P ∩ Q.
The number of distinct elements contained in a finite set A is called its cardinal number. It is denoted by n(A). For example, the number of elements in the set R = {2, 3, 5, 7} is denoted by n(R). This number is called the cardinal number of the set R.
If A and B are disjoint sets, then n(AUB) = n(A) + n(B) as n (A ∩ B) = 0
For three sets P, Q and R

When P, Q and R are disjoint sets
= n(P) + n(Q) + n(R)
Illustration: If A = {2, 3, 5, 7} , then n(A) = 4
Equivalent Set: Two finite sets A & B are said to be equivalent if n (A) = n(B).
Clearly, equal sets are equivalent but equivalent sets need not be equal.
Illustration: The sets A = {1, 3, 5} and B = {2, 4, 6} are equivalent but not equal.
Here n (A) = 3 = n (B) so they are equivalent sets. But the elements of A are not in B. Hence they are not equal though they are equivalent.
Power Set : The collection of all possible subsets of a given set A is called the power set of A, to be denoted by P(A).
Illustration: (i) If A = {1, 2, 3} then
P(A) = { {1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}, Φ }
(ii)If A = {1, {2}}, we may write A = {1, B} when B = {2} then
P(A) = { Φ , {1}, {B }, {1, B}} = { Φ , {1}, {{2}}, {1,{2}}}
Product of Sets
Ordered Pair : Two elements a and b, listed in a specific order, form an ordered pair, denoted by (a, b).Cartesian Product of sets : If A and B are two non-empty sets, then the set of all ordered pairs (a, b) such that a belongs to A and b belongs to B , is called the Cartesian product of A and B, to be denoted by A × B.
Thus, A × B = {(a, b) : a ∈ A and b ∈ B}
If A = Φ or B = Φ , we define A × B = Φ
Illustration: Let A = {1, 2, 3}, B = {4, 5}
Then A × B = { (1, 4), (1, 5), (2, 4) (2, 5), (3, 4), (3, 5) }
Example: If A × B = { ( 3, 2 ) , (3, 4) , (5, 2), (5, 4) } , find A and B.
Solution: Clearly A is the set of all first co-ordinates of A × B, while B is the set of all second co-ordinates of elements of A × B.
Therefore A = {3, 5} and B = {2 , 4}
Example: Let P = {1, 3, 6} and Q {3, 5}
The product set P × Q = {(1, 3), (1, 5), (3, 3), (3, 5), (6, 3), (6, 5)} .
Notice that n(P×Q) = n(P) × n(Q) and ordered pairs (3, 5) and (5, 3) are not equal.
and Q × P = {(3, 1), (3, 3), (3, 6), (5, 1), (5, 3), (5, 6)}
So P × Q ≠ Q × P; but n (P × Q) = n (Q × P).
Illustration: Here n(P) = 3 and n(Q ) = 2, n (P × Q) = 6. Hence n(P×Q) = n(P) × n(Q). and n(P × Q ) = n(Q × P) = 6.
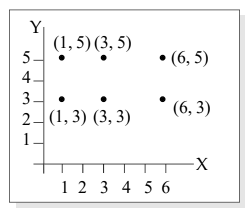 We can represent the product set of ordered pairs by plotting points in the XY plane.
We can represent the product set of ordered pairs by plotting points in the XY plane.
If X = Y = the set of all natural numbers, the product set XY represents an infinite equal lattice of points in the first quadrant of the XY plane.
Relations and Functions
Any subset of the product set X.Y is said to define a relation from X to Y and any relation from X to Y in which no two different ordered pairs have the same first element is called a function. Let A and B be two non-empty sets. Then, a rule or a correspondence f which associates to each element x of A, a unique element, denoted by f(x) of B , is called a function or mapping from A to B and we write f : ABThe element f(x) of B is called the image of x, while x is called the pre-image of f (x).
Domain & Range of a Function
Understanding Functions
- Function Definition: Let f be a function from set A to set B. Here, A is known as the domain of f, and B is called the co-domain.
- Range of Function: The set f(A) = {f(x) : x ∈ A} is called the range of f.
- Example: Consider A = {1, 2, 3, 4} and B = {1, 4, 9, 16, 25}. If we define f(x) = x², we get:
- f(1) = 1
- f(2) = 4
- f(3) = 9
- f(4) = 16
- Unique Mapping: Each element in A has a distinct image in B, confirming that f: A → B is a function. Therefore, the domain of f is {1, 2, 3, 4} and the range is {1, 4, 9, 16}.
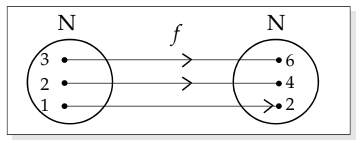
- Natural Numbers Example:
 Let N be all natural numbers. The function f(x) = 2xmaps:
Let N be all natural numbers. The function f(x) = 2xmaps: - f(1) = 2
- f(2) = 4
- f(3) = 6
- Domain and Range: Here, the domain of f is N = {1, 2, 3, ...} and the range is {2, 4, 6, ...}.
- Mapping Diagram: This function can be illustrated using a mapping diagram.
- One-One Function: A function f: A → B is one-one or injective if different elements in A map to different elements in B.
- Example: Let A = {1, 2, 3} and B = {2, 4, 6} with f(x) = 2x.
- Then f(1) = 2, f(2) = 4, and f(3) = 6. This shows that f is one-one.
- Important Note: For f: A → B, if x1 = x2, then f(x1) = f(x2). If f(x1) = f(x2), this implies x1 = x2 only if f is one-one.
- Onto Functions: A function f: A → B is onto or surjective if every element in B has at least one corresponding element in A.
- Condition: For each y ∈ B, there must be at least one x ∈ A such that y = f(x).
- Example: Let N be natural numbers and E be even natural numbers. The function f: N → E defined by f(x) = 2x is onto, since every element in E is of the form 2x.
- Bijection Function: A function that is both one-one and onto is termed bijective, also known as a one-to-one correspondence.
- Identity Function: For a non-empty set A, the function I: A → A defined by I(x) = x is called an identity function as it is one-one and onto.
- Into Functions: If there is even one element in B that has no pre-image in A, then f is considered an into function.
- Example: Let A = {2, 3, 5, 7} and B = {0, 1, 3, 5, 7}, with f(x) = x - 2. Here, f(2) = 0, f(3) = 1, f(5) = 3, and f(7) = 5.
- Since there is an element 7 in B that has no pre-image in A, f is an into function.
- Constant Function: A function f: A → B is called a constant function if all elements in A map to the same element in B.
- Example: If A = {1, 2, 3} and B = {5}, then f(x) = 5 for all x ∈ A.
- Equal Functions: Two functions f and g are equal if they have the same domain and f(x) = g(x) for all x.
- Composite Function: Given two functions n: X → Y and g: Y → Z, the composite function g(n(x)) is defined as g(n(1)) = 3.
- Inverse Function: If f is a one-one and onto function from set A to set B, then the inverse function f-1: B → A can be defined, where f-1(y) = x if and only if f(x) = y.
Different types of relations
Let S = {a, b, c, ….} be any set then the relation R is a subset of the product set S×S
i) If R contains all ordered pairs of the form (a, a) in S×S, then R is called reflexive. In a reflexive relation 'a' is related to itself .
For example, 'Is equal to' is a reflexive relation for a = a is true.
ii) If (a, b)∈R ⇒ (b, a)∈ R for every a, b∈S then R is called symmetric For example a∈b⇒ b = a. Hence the relation 'is equal to' is a symmetric relation.
iii) If (a, b)∈R and (b, c)∈R ⇒ (a, c) ∈ R for every a, b, c, ⇒S then R is called transistive. For example a =b, b=c ⇒ a=c. Hence the relation 'is equal to' is a transitive relation. A relation which is reflexive, symmetric and transitive is called an equivalence relation or simply an equivalence. 'is equal to' is an equivalence relation.
Similarly, the relation " is parallel to " on the set S of all straight lines in a plane is an equivalence relation.
Illustration: The relation "is parallel to" on the set S is
(1) reflexive, since a || a for a ∈ S
(2) symmetric, since a || b ⇒ b || a
(3) transitive, since a || b , b || c ⇒ a || c
Hence it is an equivalence relation.
Domain & Range of a relation : If R is a relation from A to B, then the set of all first coordinates of elements of R is called the domain of R,
- The set of all second elements in the pairs of a relation R is known as the range of R.
- The domain of R is defined as: Dom(R) = { a : (a, b) ∈ R } and the range of R is: Range(R) = { b : (a, b) ∈ R }.
- For example, let A = {1, 2, 3} and B = {2, 4, 6}. Then, the product set A × B is: A × B = {(1, 2), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 2), (3, 4), (3, 6)}.
- By definition, any subset of A × B represents a relation from A to B.
- Considering the relation: R = {(1, 2), (1, 4), (3, 2), (3, 4)}, we find: Dom(R) = {1, 3} and Range(R) = {2, 4}.
- From the product set X × Y = {(1, 3), (2, 3), (3, 3), (4, 3), (2, 2), (3, 2), (4, 2), (1, 1), (2, 1), (3, 1), (4, 1)}, different subsets define various relations:
- Is equal to: {(1, 1), (2, 2), (3, 3)}
- Is less than: {(1, 3), (2, 3), (1, 2)}
- Is greater than: {(4, 3), (3, 2), (4, 2), (2, 1), (3, 1), (4, 1)}
- Is greater than or equal to: {(4, 3), (3, 2), (4, 2), (2, 1), (3, 1), (4, 1), (1, 1), (2, 2), (3, 3)}
- Again, let A = {1, 2, 3} and B = {2, 4, 6}. For the relation: R = {(1, 2), (1, 4), (3, 4)}, we have: Dom(R) = {1, 3} and Range(R) = {2, 4}, which represents the relation Is less than.
- The identity relation is defined as: I = {(a, a) : a ∈ A}.
- For example, if A = {1, 2, 3}, then: I = {(1, 1), (2, 2), (3, 3)}.
- An inverse relation of R is defined as: R-1 = {(b, a) : (a, b) ∈ R}.
- It follows that: Dom(R-1) = Range(R) and Range(R-1) = Dom(R).
- For example, let A = {1, 2, 3} and R = {(1, 2), (2, 2), (3, 1), (3, 2)}. Here, R is a subset of A × A, which means it is a relation on A. We find: Dom(R) = {1, 2, 3} and Range(R) = {2, 1}. The inverse relation is: R-1 = {(2, 1), (2, 2), (1, 3), (2, 3)}. Thus, Dom(R-1) = {2, 1} = Range(R) and Range(R-1) = {1, 2, 3} = Dom(R).
- Consider the following relations on A = {1, 2, 3}:
- R1 = {(1, 1), (2, 2), (3, 3), (1, 2)} is reflexive and transitive but not symmetric, since (1, 2) is in R1 but (2, 1) is not.
- R2 = {(1, 1), (2, 2), (1, 2), (2, 1)} is symmetric and transitive but not reflexive, as (3, 3) is not in R2.
- R3 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 2)} is reflexive and symmetric but not transitive, because (1, 2) and (2, 3) are in R3, but (1, 3) is not.
Problems and solution using Venn Diagram
1. Out of a group of 20 teachers in a school, 10 teach Mathematics, 9 teach Physics and 7 teach Chemistry. 4 teach Mathematics and Physics but none teach both Mathematics and Chemistry. How many teach Chemistry and Physics? How many teach only Physics ?
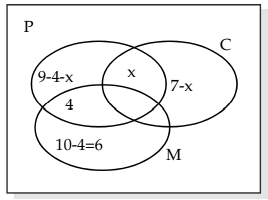
Solution:
Let x be the no. of teachers who teach both Physics & Chemistry.
9 – 4 – x + 6 + 7 – x + 4 + x = 20
or 22 – x = 20
or x = 2
Hence, 2 teachers teach both Physics and Chemistry and 9 – 4 – 2 = 3 teachers teach only Physics.
2. A survey shows that 74% of the Indians like grapes, whereas 68% like bananas.
What percentage of the Indians like both grapes and bananas?
Solution: Let P & Q denote the sets of Indians who like grapes and bananas respectively. Then n(P ) = 74, n(Q) = 68 and n(P ∪ Q) = 100.
We know that n( P ∩ Q) = n(P) + n(Q) – n( P ∪ Q )
= 74 + 68 – 100
= 42.
Hence, 42% of the Indians like both grapes and bananas.
3. In a class of 60 students, 40 students like Maths, 36 like Science, and 24 like both the subjects. Find the number of students who like
(i) Maths only
(ii) Science only
(iv) neither Maths nor Science
(iii) either Maths or Science
Solution: Let M = students who like Maths and S = students who like Science
Then n( M) = 40, n(S) = 36 and n (M ∩ S ) = 24
Hence,
(i) n(M) – n(M ∩ S) = 40 – 24 = 16 = number of students like Maths only.
(ii) n( S ) – n(M ∩ S) = 36 – 24 = 12 = number of students like Science only.
(iii) n(M∪ S) = n(M) + n(S) – n(M ∪ S) = 40 + 36 – 24 = 52 = number of students who like either Maths or Science.
(iv) n(M ∪ S)c = 60 – n(M ∪ S ) = 60 – 52 = 8 = number of students who like neither Maths nor Science.
|
114 videos|164 docs|98 tests
|
FAQs on Sets, Relations and Functions Chapter Notes - Quantitative Aptitude for CA Foundation
| 1. What is a set and how is it defined in mathematics? |  |
| 2. How are Venn diagrams used to represent sets? |  |
| 3. What is the product of sets and how is it calculated? |  |
| 4. What are the different types of relations in mathematics? |  |
| 5. How do you determine the domain and range of a function? |  |
|
114 videos|164 docs|98 tests
|

|
Explore Courses for CA Foundation exam
|

|
 Let N be all natural numbers. The function f(x) = 2xmaps:
Let N be all natural numbers. The function f(x) = 2xmaps: 
















