Sets Chapter Notes | Mathematics Class 8 ICSE PDF Download
Introduction
Sets are a fundamental concept in mathematics, serving as the building blocks for organizing and understanding collections of objects. In this chapter, we explore the concept of sets, their representation, types, and operations. We learn how to define sets clearly, represent them in different forms, and perform operations like union, intersection, and difference. The chapter also covers subsets, proper subsets, universal sets, complement sets, and properties like distributive laws and De Morgan's laws. Additionally, it introduces Venn diagrams to visualize relationships between sets, providing a comprehensive understanding of how sets work and their applications in solving problems.
Set
- A set is a collection of clearly defined objects, such as numbers, names, or items.
- Objects must be specific for the collection to qualify as a set.
- Example: The collection of students with heights between 135 cm and 160 cm is a set because it is well-defined.
- Counter example: The collection of "tall students" is not a set because "tall" is subjective and not clearly defined.
Elements
- Elements or members are the individual objects that make up a set.
- Sets are usually denoted by capital letters (e.g., A, B, V).
- Elements are written inside curly braces { } and separated by commas.
- Examples:
- Set A = {John, Geeta, Amit, Rohit} represents a set of names.
- Set V = {a, e, i, o, u} represents the vowels of the English alphabet.
- The symbol ∈ means "belongs to," e.g., a ∈ V means "a" is an element of set V.
- The symbol ∉ means "does not belong to," e.g., b ∉ V means "b" is not an element of set V.
Representation of a Set
Sets can be represented in two main ways: Roster Form and Set-Builder Form.
Roster (or Tabular) Form
- In Roster Form, all elements of the set are listed inside curly braces { }, separated by commas.
- Examples:
- Set A = {2, 5, 7, 9, 15} lists the numbers directly.
- Set of integers Z = {…, -2, -1, 0, 1, 2, 3, …}.
- Set of whole numbers W = {0, 1, 2, 3, 4, …}.
- Set of natural numbers N = {1, 2, 3, 4, …}.
- The order of elements does not matter, e.g., {a, b, c} is the same as {b, a, c}.
- Each element is written only once, e.g., {2, 3, 3, 2, 4} is simplified to {2, 3, 4}.
- Example: The set of letters in "ALLAHABAD" is {a, l, h, b, d}, with no duplicates.
Set-Builder Form (Rule Method)
- In Set-Builder Form, a rule or formula describes the elements of the set without listing them.
- Format: {x : condition on x}, read as "the set of all x such that the condition holds."
- Examples:
- A = {x : x ∈ N and x < 7} describes natural numbers less than 7, which is {1, 2, 3, 4, 5, 6}.
- Set A = {2, 3, 4, 5} can be written as {x : x ∈ N, 2 ≤ x < 6} or {x : x ∈ N, 1 < x ≤ 5}.
- Set C = {1, 3, 5, 7, 9, 11} can be written as {x : x = 2n-1, n ∈ N, n ≤ 6} or {x : x = 2n+1, n ∈ W, n ≤ 5}.
- Set D = {2, 4, 6, 8} can be written as {x : x = 2n, n ∈ N, n ≤ 4}.
Cardinal Number of a Set
- The cardinal number of a set is the number of elements it contains, denoted by n(A).
- Examples:
- For A = {c, d, f}, n(A) = 3.
- For B = {2, 4, 5, 6}, n(B) = 4.
Types of Sets
Sets can be classified based on the number and nature of their elements.
Finite Set
- A set with a limited number of elements is called a finite set.
- Examples:
- The set of boys in a class.
- {x : x is a member of a particular family}.
- {3, 4, 5, …, 100} has 98 elements.
Infinite Set
- A set with an unlimited number of elements is called an infinite set.
- Examples:
- {x : x is a living thing}.
- {x : x ∈ W and x > 1000}.
Singleton or Unit Set
- A set with exactly one element is called a singleton or unit set.
- Examples:
- {x : x is President of India}.
- The set of whole numbers between 6 and 8 is {7}.
- {x : 2x - 1 = 3} is {2}.
Empty or Null Set
- A set with no elements is called an empty or null set, denoted by Ø (pronounced "oe").
- Examples:
- The set of odd numbers between 7 and 9 is Ø.
- {x : x ∈ N and x < 1} is Ø.
- The cardinal number of the empty set is 0, i.e., n(Ø) = 0.
Note:
- {0} is not empty because it contains the element 0.
- {Ø} is not empty because it contains the empty set as an element.
Joint or Overlapping Sets
- Two sets are joint or overlapping if they have at least one element in common.
- Example: A = {5, 7, 9, 11} and B = {6, 9, 12, 15} are overlapping because 9 is common.
Disjoint Sets
- Two sets are disjoint if they have no elements in common.
- Examples:
- A = {5, 7, 9, 11} and B = {4, 6, 8, 10} are disjoint.
- A = {students of Sophia Girls' School} and B = {students of St. Mary's Academy} are disjoint.
Equivalent Sets
- Two sets are equivalent if they have the same number of elements, denoted by A ↔ B.
- Example: A = {a, b, c} and B = {x, y, z} are equivalent because n(A) = n(B) = 3.
Equal Sets
- Two sets are equal if they contain exactly the same elements.
- Example: A = {1, 2, 3, 4, 5} and B = {x : x ∈ N and x < 6} are equal because they have identical elements.
Note: Equal sets are always equivalent, but equivalent sets are not necessarily equal.
Subset
- A set A is a subset of set B if every element of A is also in B, denoted by A ⊆ B.
- A ⊆ B is read as "A is a subset of B" or "A is contained in B."
- Examples:
- A = {5, 6, 7} and B = {2, 3, 4, 5, 6, 7}, so A ⊆ B.
- If A = {students of a school} and B = {class VIII students of the school}, then B ⊆ A.
- If P = {even natural numbers} and Q = {multiples of 4}, then Q ⊆ P.
- Every set is a subset of itself, e.g., A ⊆ A.
- The empty set Ø is a subset of every set, e.g., Ø ⊆ A.
- If A ⊆ B and B ⊆ A, then A = B.
Proper Subset
- A set A is a proper subset of set B if all elements of A are in B and B has at least one element not in A, denoted by A ⊂ B.
- A ⊂ B is read as "A is a proper subset of B."
- Examples:
- A = {5, 6, 7} and B = {3, 5, 6, 7, 8}, so A ⊂ B.
- The set of natural numbers N is a proper subset of whole numbers W, i.e., N ⊂ W.
Number of Subsets and Proper Subsets of a Given Set
- For a set with n elements:
- The number of subsets is 2n.
- The number of proper subsets is 2n - 1.
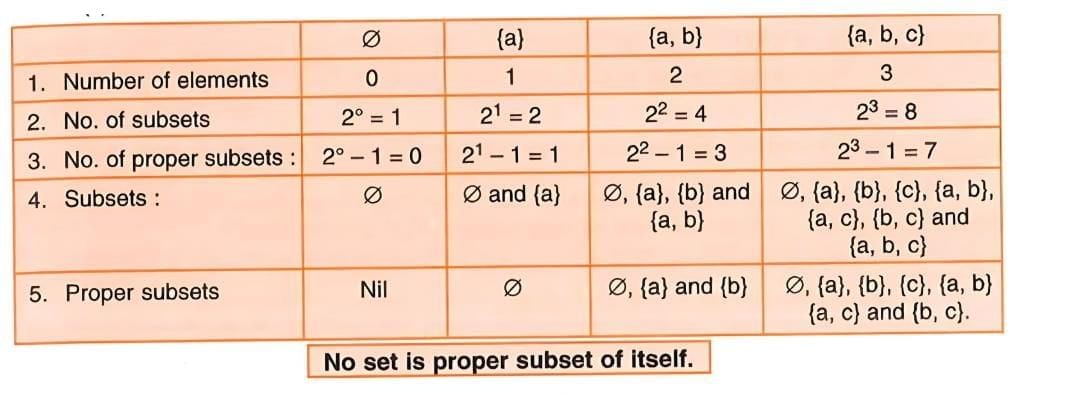
- Examples:
- For a set with 0 elements (Ø), number of subsets = 20 = 1, proper subsets = 0.
- For {a}, number of subsets = 21 = 2 (Ø, {a}), proper subsets = 1 (Ø).
- For {a, b}, number of subsets = 22 = 4 (Ø, {a}, {b}, {a, b}), proper subsets = 3 (Ø, {a}, {b}).
- For {a, b, c}, number of subsets = 23 = 8 (Ø, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}), proper subsets = 7 (all except {a, b, c}).
- No set is a proper subset of itself.
Super Set
- If A is a subset of B, then B is a super set of A, denoted by B ⊇ A.
- B ⊇ A is read as "B is a super set of A."
Universal Set
- A universal set contains all sets under consideration as its subsets, denoted by ξ or U.
- Examples:
- For A = {5, 6, 7, 8}, B = {1, 3, 5, 7}, C = {4, 6, 8, 10}, a universal set could be {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. The choice of a universal set is not unique.
- For A = {2, 4, 6, 7}, B = {3, 5, 7, 9, 11}, C = {0, 4, 8, 12, 16}, possible universal sets include {x : x ∈ W and x ≤ 16}, {x : x ∈ W}, or {x : x ∈ Z, 0 ≤ x < 17}.
- For D = {students of class 9}, possible universal sets include {students of the school} or {students of the town}.
Complement Set
- The complement of a set A, denoted A', is the set of all elements in the universal set ξ that are not in A.
- Examples:
- If ξ = {1, 2, 3, 4, 5, 6} and A = {2, 3, 5}, then A' = {1, 4, 6}.
- If ξ = {x : x ∈ N} and A = {even natural numbers}, then A' = {odd natural numbers}.
- A set and its complement are disjoint, meaning they have no common elements.
- The complement of the empty set is the universal set, i.e., Ø' = ξ.
- The complement of the universal set is the empty set, i.e., ξ' = Ø.
Set Operations
Union of Two Sets
- The union of sets A and B, denoted A ∪ B, includes all elements that are in A, in B, or in both.
- Examples:
- If A = {5, 6, 7} and B = {6, 8}, then A ∪ B = {5, 6, 7, 8}.
- If E = {numbers divisible by 2} and F = {numbers divisible by 3}, then E ∪ F = {numbers divisible by 2 or 3 or both}.
- Union is commutative: A ∪ B = B ∪ A.
- Union is associative: A ∪ (B ∪ C) = (A ∪ B) ∪ C.
- A is a subset of A ∪ B, i.e., A ⊂ (A ∪ B).
- If A ⊂ B, then A ∪ B = B.
- The union of a set and its complement is the universal set: A ∪ A' = ξ.
- The union of a set and the empty set is the set itself: A ∪ Ø = A.
- The union of a set and the universal set is the universal set: A ∪ ξ = ξ.
Intersection of Two Sets
- The intersection of sets A and B, denoted A ∩ B, includes all elements common to both A and B.
- Examples:
- If A = {5, 6, 7} and B = {6, 8}, then A ∩ B = {6}.
- If E = {numbers divisible by 2} and F = {numbers divisible by 3}, then E ∩ F = {numbers divisible by 6}.
- Intersection is commutative: A ∩ B = B ∩ A.
- Intersection is associative: A ∩ (B ∩ C) = (A ∩ B) ∩ C.
- A ∩ B is a subset of A and B: (A ∩ B) ⊂ A and (A ∩ B) ⊂ B.
- If A and B are disjoint, then A ∩ B = Ø.
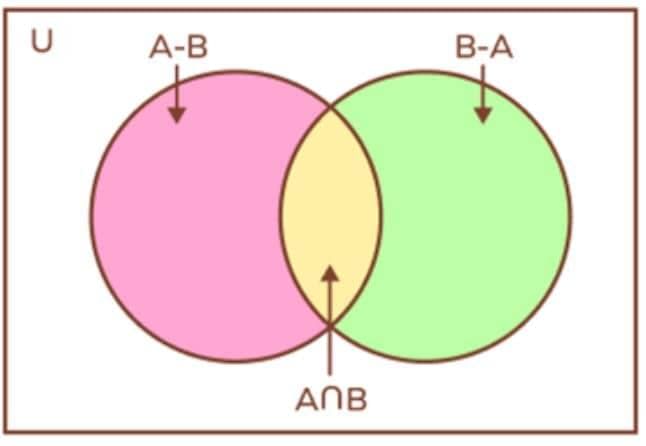
Difference of Two Sets
- The difference of sets A and B, denoted A - B or A \ B, is the set of elements that are in A but not in B.
- It is also written as A - B = {x : x ∈ A and x ∉ B}.
- Examples:
- If A = {5, 6, 7} and B = {6, 8}, then A - B = {5, 7}.
- If A = {1, 2, 3, 4} and B = {2, 4, 6}, then A - B = {1, 3}.
- The difference is not commutative: A - B ≠ B - A.
- Example: For the above sets, B - A = {6}.
- If A and B are disjoint, then A - B = A.
- If A ⊆ B, then A - B = Ø.
Distributive Laws
Distributive laws describe how union and intersection operations distribute over each other.
- First Distributive Law: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
- This means the union of A with the intersection of B and C is the same as the intersection of the unions of A with B and A with C.
- Second Distributive Law: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
- This means the intersection of A with the union of B and C is the same as the union of the intersections of A with B and A with C.
De Morgan's Laws
De Morgan's laws relate the complement of unions and intersections of sets.
- First De Morgan's Law:(A ∪ B)' = A' ∩ B'.
- This means the complement of the union of A and B is the intersection of their complements.
- Second De Morgan's Law:(A ∩ B)' = A' ∪ B'.
- This means the complement of the intersection of A and B is the union of their complements.
- Example: If ξ = {1, 2, 3, 4, 5}, A = {1, 2}, B = {2, 3}, then (A ∪ B)' = {4, 5} = A' ∩ B', and (A ∩ B)' = {1, 3, 4, 5} = A' ∪ B'.
Cardinal Property
- The cardinal property helps calculate the number of elements in the union of two sets.
- Formula: n(A ∪ B) = n(A) + n(B) - n(A ∩ B).
- This accounts for elements counted twice in A and B by subtracting the number of common elements.
- Example: If n(A) = 20, n(B) = 25, and n(A ∩ B) = 10, then n(A ∪ B) = 20 + 25 - 10 = 35.
- For three sets: n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(A ∩ C) + n(A ∩ B ∩ C).
Venn Diagram
- A Venn diagram is a visual tool to represent sets and their relationships using circles within a rectangle (the universal set).
- Each circle represents a set, and the rectangle represents the universal set ξ.
- Overlapping circles indicate common elements (intersection).
- Example: For A = {5, 6, 7} and B = {6, 8}, the Venn diagram shows 6 in the overlapping region, 5 and 7 in A’s circle, and 8 in B’s circle.
- Union (A ∪ B) is represented by the entire area covered by both circles.
- Intersection (A ∩ B) is the overlapping area.
- Complement (A') is the area outside A’s circle but within the universal set.
- Difference (A - B) is the part of A’s circle not overlapping with B.
Using Venn Diagram to Show Relationship Between Sets
- Venn diagrams illustrate relationships like subsets, unions, intersections, and differences.
- For overlapping sets A and B, the diagram shows:
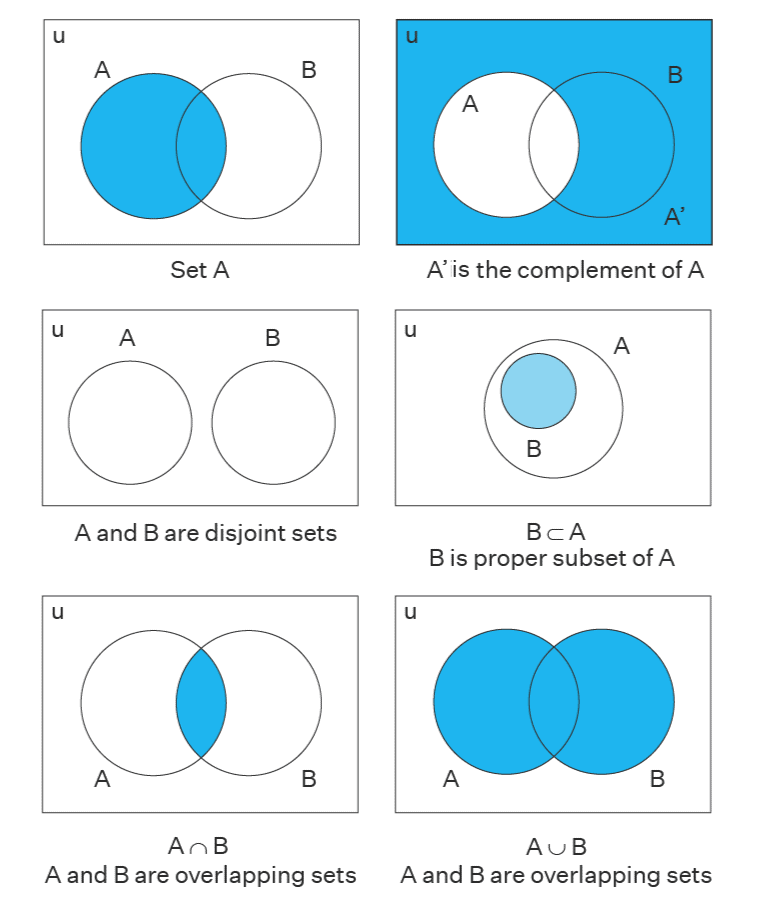
- A ∩ B as the common region.
- A ∪ B as the combined region of both circles.
- (A ∩ B)' as the area outside the common region but within ξ.
- (A ∪ B)' as the area outside both circles but within ξ.
- A' ∩ B as the part of B’s circle not in A.
- For disjoint sets, circles do not overlap, and A ∩ B = Ø.
- For subsets, one circle (A) is completely inside another (B) if A ⊆ B.
- A - B as the part of A’s circle not in B.
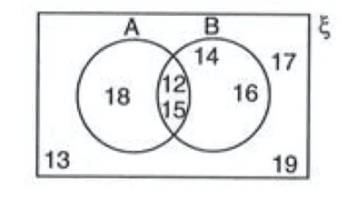
- Example: If ξ = {12, 13, 14, 15, 16, 17, 18, 19}, A = {12, 15, 18}, B = {12, 14, 15, 16}, the Venn diagram shows 12 and 15 in the overlapping region, 18 in A’s circle, and 14 and 16 in B’s circle.
|
23 videos|98 docs|14 tests
|
FAQs on Sets Chapter Notes - Mathematics Class 8 ICSE
| 1. What is a set in mathematics? |  |
| 2. How do you determine the cardinal number of a set? |  |
| 3. What is the difference between a subset and a proper subset? |  |
| 4. How do you find the number of subsets of a given set? |  |
| 5. What is a universal set and a complement set? |  |




















