Weaving Mats
You may have seen woven baskets of different kinds. If you look closely, you will notice different weaving patterns on each basket.
We will try weaving some mats with paper strips.
You will need - A coloured paper (30 cm long and 20 cm wide) and eight paper strips of two different colours (3 cm wide and longer than 20 cm).
(a) Take a coloured paper 30 cm long and 20 cm wide.
(b) Fold the coloured paper in half along the longer side.
(c) Draw vertical lines at equal distances from the closed end and cut slits, leaving a gap of 3 cm at the top.
(d) Carefully unfold the paper. There will be no cuts in the paper at the top and the bottom.
(e) Now cut 8 paper strips of 3 cm width in 2 colours and of length slightly longer than 20 cm.
(f) Take one colour strip and weave it across the slits, going 1 under and 1 over, and again 1 under and 1 over. Repeat it for the first row.
(g) Take one more strip of another colour and weave it across the slits, going 1 over and 1 under, and again 1 over and 1 under. Repeat it for the second row.
(h) Weave all the strips in the same alternating pattern. Neatly fold any extra strip ends behind the mat. Your mat is ready!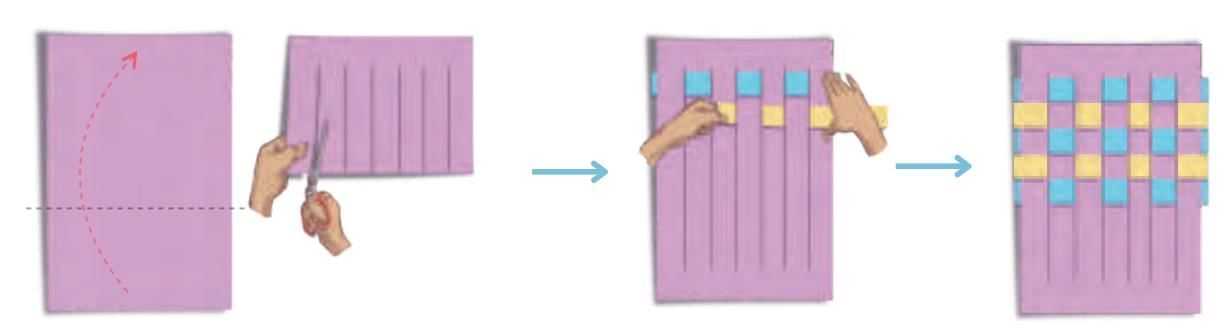

Just as numbers and colours can form patterns, we can also create beautiful repeating designs by weaving strips of paper into mats.
Patterns
- A pattern is something that repeats in the same way again and again, and by knowing its rule, we can predict what comes next.
- Patterns can be made with colours, shapes, or numbers, like red–blue–red–blue or 2, 4, 6, 8.
- We can see patterns all around us in daily life, such as in clothes, tiles, zebra stripes, flower petals, or honeycombs.
- Patterns are useful because they help us organise information, solve problems easily, and make predictions.
Different Types of Shapes
1. Square
- A square has 4 equal sides.
- All 4 angles are 90° (right angles).
- It looks like a perfect box.
- Examples: Floor tiles, a chessboard, a carrom board.
2. Rectangle 
- A rectangle has 4 sides.
- Opposite sides are equal, and all angles are 90°.
- It is longer in one direction.
- Examples: Doors, windows, books.
3. Triangle 
- A triangle has 3 sides and 3 angles.
- The sides and angles can be equal or unequal.
- It is the simplest closed shape.
- Examples: Pyramids, road signboards.
4. Rhombus
- A rhombus has 4 equal sides.
- Angles are not 90°.
- It looks like a “slanted square.”
- Examples: Diamond shapes on kites, quilt designs.
5. Parallelogram
- A parallelogram has 4 sides.
- Opposite sides are equal and parallel, but the angles are not 90°.
- It looks like a “slanted rectangle.”
- Examples: Slanted roof designs, some windows.
6. Trapezium
- A trapezium has 4 sides.
- One pair of opposite sides is parallel, and the other pair is not.
- Examples: Trapezoid tables, roof edges.
7. Circle
- A circle has no sides and no corners.
- It is a perfect round shape.
- The angle around it is 360°.
- Examples: Wheels, bangles, coins.
8. Pentagon 
- A pentagon has 5 sides and 5 angles.
- The sides may or may not be equal.
- Examples: Pentagon building, star designs.
9. Hexagon
- A hexagon has 6 sides and 6 angles.
- Often, all sides are equal.
- Examples: Honeycombs, hexagonal tiles.
10. Octagon
- An octagon has 8 sides and 8 angles.
- Often used in road signs.
- Examples: Stop sign, star patterns.
Key Idea:- Shapes are different because of their sides and angles.
- Squares and rectangles have right angles, while shapes like rhombus and parallelogram have slanted angles.
- Circles are special because they have no sides but are still a closed shape.
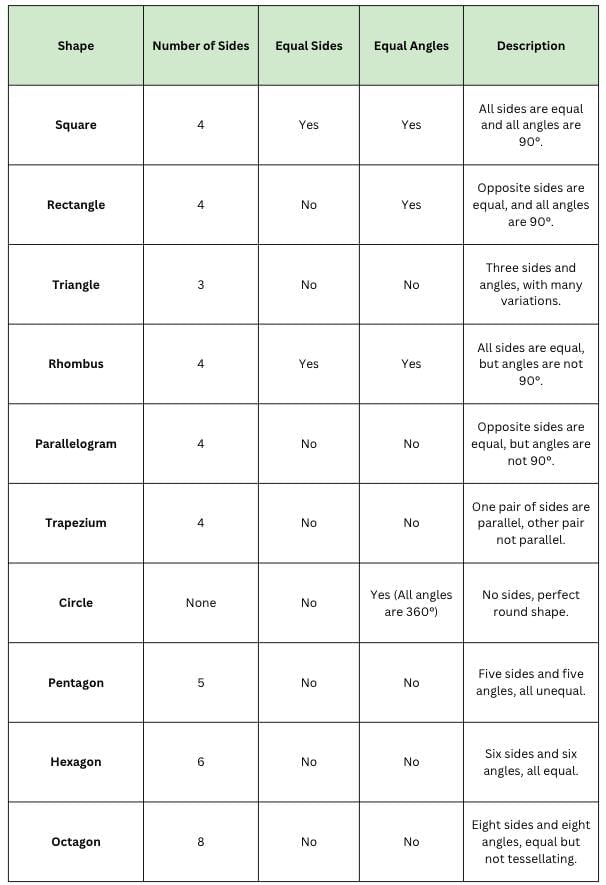
Tiling and Tessellation
- Tiling: Using shapes (like tiles) to cover a surface without gaps or overlaps.
- Regular Shapes: Shapes with equal sides, like squares, triangles, and pentagons.
- Pentagons: A regular pentagon has 5 equal sides.
- When we place 3 pentagons around a point, there’s a space left.
- Pentagons cannot tessellate because they don’t fit together perfectly—they leave gaps.
- Tessellation happens when shapes fit together without any gaps or overlaps, like squares or triangles.
Find Out
Can regular triangles fit together at a point without any gap? How many of them fit together? Do you see that regular triangles fit around a point as shown here?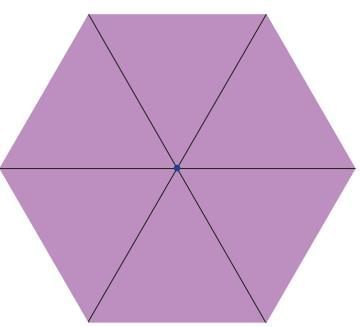
Regular triangles, when fitted around a point, leave no gaps, and there is no overlap.
Triangles with all equal sides are also called equilateral triangles. Therefore, equilateral triangles tessellate.
Sol:
- Yes! Equilateral triangles (triangles with all equal sides) fit together perfectly around a point without any gaps or overlaps.
- Exactly 6 equilateral triangles fit together around a point. When placed correctly, they create a tessellating pattern with no empty spaces.
Can five squares fit together around a point without any gaps or overlaps? Why or why not?

Sol:
- Yes, squares (4-sided shapes) also fit together perfectly around a point without gaps or overlaps. You will need 4 squares to fit together around a point.
- No, 5 squares cannot fit together at a point because there isn’t enough space to align them without leaving gaps.
Can regular hexagons (6-sided shapes with equal sides) fit together around a point without any gaps or overlaps? Try and see (a sample hexagon is given at the end of the book). How many fit together at a point?
Sol: Yes, regular hexagons (6-sided shapes) fit together perfectly around a point, with 3 hexagons fitting together at each point without any gaps or overlaps.
Here is a tessellating pattern with more than one shape.
What shapes have been used in this pattern? _____________, _____________.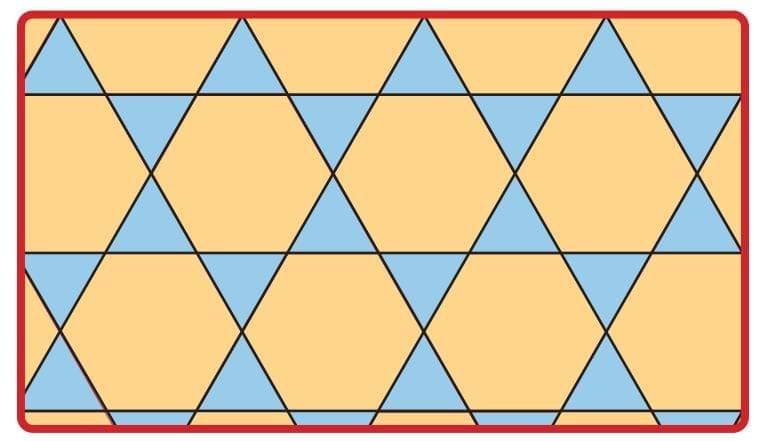
Sol: Triangles, Regular Hexagon
A regular octagon means a shape with eight equal sides. Do regular octagons fit together without any gaps or overlaps? Try drawing the same and check
Sol: Regular octagons do not tessellate.
Because:
The angles inside an octagon are too big to fit together perfectly at the corners.
When you place octagons next to each other, they leave gaps because their angles don’t match up to fill the space completely.
A rhombus is a shape with all equal sides.
What shapes are coming together at the marked points? Are the same set of shapes coming together at these points?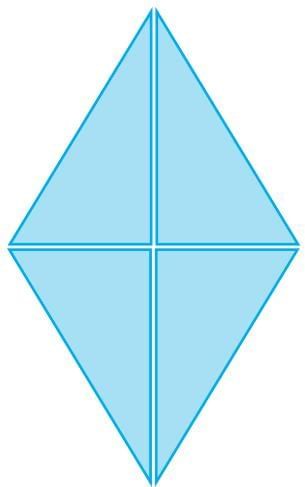
Sol:
- At the marked points, we can see rhombuses and triangles coming together.
- Yes, the same set of shapes (rhombuses and triangles) is repeating at each marked point. This means the pattern is consistent and repeating.
- Rhombuses have equal sides, and when divided into four triangles, the angles of the triangles match up perfectly with each other. This helps the shapes fit together neatly without any gaps.
- The equal sides and angles of rhombuses and triangles allow them to fill a surface by repeating without leaving any empty spaces. This is why tessellation works — the shapes fit together perfectly and create a pattern.
Types of Triangles
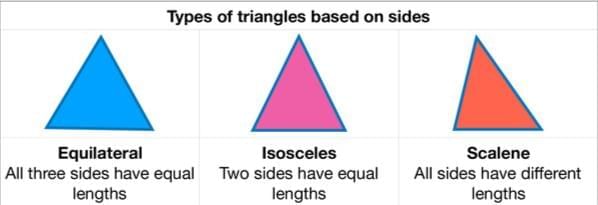
- Equilateral Triangle
- All three sides are equal.
- All three angles are the same and are always 60°.
- Example: A perfect triangle with all sides the same length.
- Isosceles Triangle
- Two sides are equal, and the third side is different.
- The two angles opposite the equal sides are also equal.
- Example: A triangle with two sides of the same length and one different.
- Scalene Triangle
- All three sides are different lengths.
- All three angles are also different.
- Example: A triangle with no equal sides or angles.
Try This
Quadrilaterals whose opposite sides are equal are called parallelograms.
What types of angles do quadrilaterals A and B have? Which angles are equal in each of the above parallelograms?
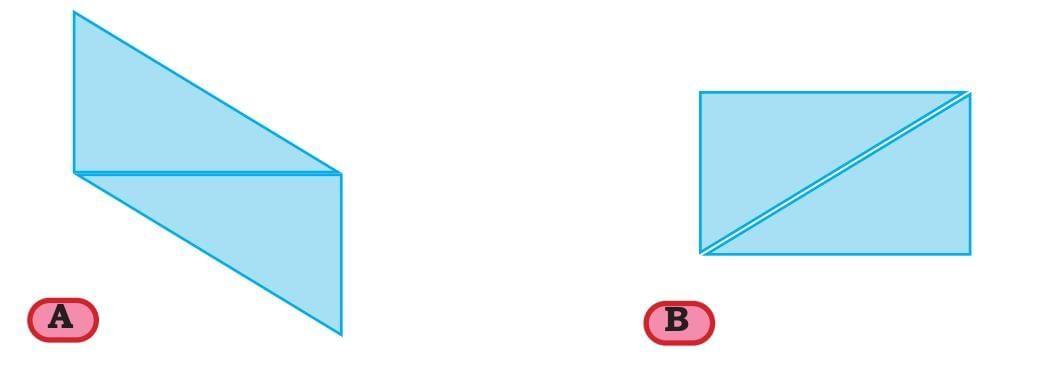
In parallelogram A, opposite angles are equal.
In parallelogram B, all angles are equal and are right angles. Such a parallelogram is called a rectangle.
A rectangle is a special type of parallelogram.
Tangram
- A Tangram is a puzzle made of 7 flat pieces (called tans) that can be rearranged to form different shapes and figures.
- Observing Angles and Sides
When you look at the Tangram pieces, you can see how the angles of each piece fit together to form new shapes.
The triangles have different angles, while the square and parallelogram have right angles.
The pieces may have equal sides or unequal sides, depending on their shape. - Using Tangram Pieces to Make Figures
You can rearrange the 7 pieces to make different shapes.
For example: a bird or a fish. - Tangrams help develop spatial thinking, which means understanding how shapes fit together and how they can be rearranged.
- Why is Tangram Fun?
Tangram puzzles are fun because you can create many different things using the same 7 pieces.
It also helps you practice problem-solving and creativity as you figure out how to arrange the pieces into new shapes.
Observe and Answer
Look at the tangram set given. Cut out all the shapes. Name them.
 (a) How are they the same or different from each other?
(a) How are they the same or different from each other?
(b) What do you notice about the angles of each of the shapes?
(c) What do you notice about the sides of each of the shapes?
Now, use some or all of the pieces of your tangram set to make the following shapes. There may be more than one way to do it.
Sol:
A standard Tangram has 7 pieces:
- 2 Large right-angled isosceles triangles
- 1 Medium right-angled isosceles triangle
- 2 Small right-angled isosceles triangles
- 1 Square
- 1 Parallelogram
(a) Same:
- All the shapes are polygons.
- Many are right-angled isosceles triangles (triangles with one right angle and two equal sides).
- Altogether, they fit perfectly into a large square.
Different:- Some shapes are triangles, one is a square, and one is a parallelogram.
- Their sizes vary (small, medium, and large triangles).
- The parallelogram is the only piece without right angles.
(b)
- Triangles: Each has a right angle (90°) and two 45° angles.
- Square: All four angles are right angles (90°).
- Parallelogram: Opposite angles are equal, not all right angles.
(c)
- Triangles: Two equal sides (isosceles).
- Square: All four sides equal.
- Parallelogram: Opposite sides equal and parallel.
Using Tangram Pieces to Make Given Shapes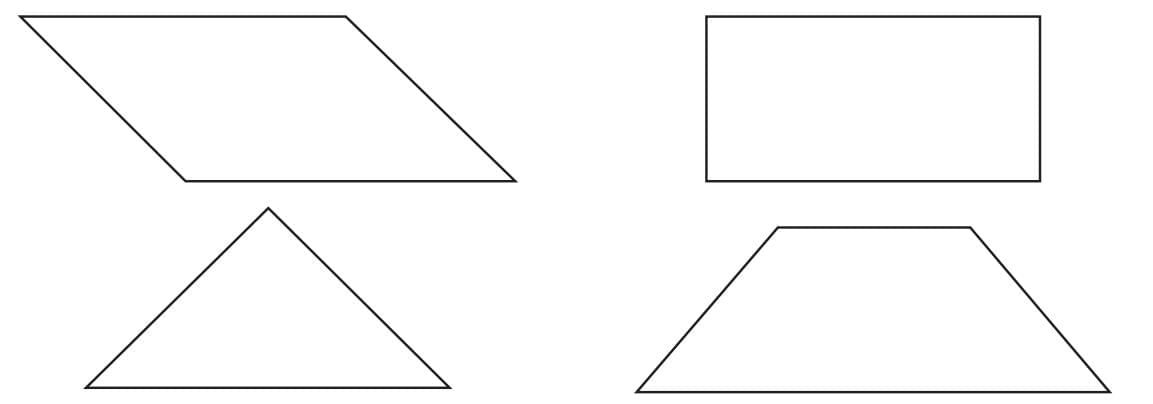
- Parallelogram (top left):
- Can be made using the parallelogram piece itself OR by combining triangles.
- Square (top right):
- Can be made using the square piece directly, or by joining two small triangles.
- Triangle (bottom left):
- Can be made using any of the triangle pieces (small, medium, or large).
- Trapezium (bottom right):
- Can be made by combining two or more triangle pieces.
Kites
- A kite is a four-sided shape with two pairs of adjacent sides that are equal in length.
- The adjacent sides are the sides that are next to each other.
- The diagonals of a kite cross each other at right angles (90°), and one diagonal bisects the other.
- The angles between the unequal sides of the kite are equal.
- You can make a kite shape by folding a square piece of paper diagonally and bringing the opposite corners together.
- Kites are also seen in real life, like the flying kites or diamond shapes.
- The name "kite" comes from the kite shape seen in flying kites!
Make your own kite shape.
(a) Start with a square piece of paper.
(b) Take one corner of the paper and fold it towards the opposite corner, creating a sharp crease along the diagonal.
(c) Open and fold the corner A inwards, aligning the edge with the crease you just made.
(d) Repeat on the other side, folding the other corner B inwards to align with the crease at the centre. 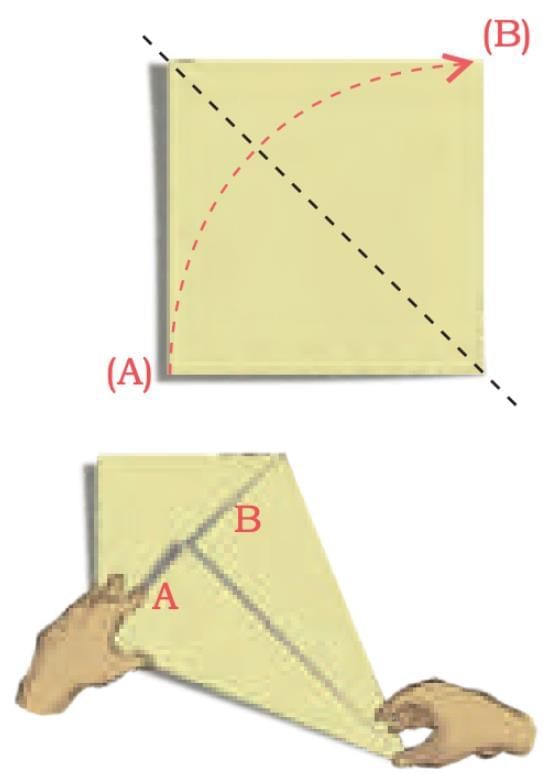 You have a kite shape! What shapes do you see in the kite
You have a kite shape! What shapes do you see in the kite
Sol: The kite shape is a quadrilateral made of two triangles and a central quadrilateral (square/diamond) formed by the folds.
Circles
- A circle is a shape with no straight sides, and every point on the circle is equidistant from the centre.
- The distance from the centre of the circle to any point on the circle is called the radius.
- The longest distance across the circle, passing through the centre, is called the diameter. The diameter is twice the length of the radius.
- The circumference is the distance around the edge of the circle.
- Circles are round and have no corners or edges.
- Every circle has 360° angles, meaning the entire angle around the circle adds up to 360 degrees.
- Pi (π) is a special number used to calculate the circumference and area of a circle.
Play with Circles
(a) Draw a circle with a compass and mark its centre.
(b) Draw its diameter. Mark the endpoints of the diameter.
(c) Draw another diameter of the circle and mark the endpoints.
(d) Now join the four points.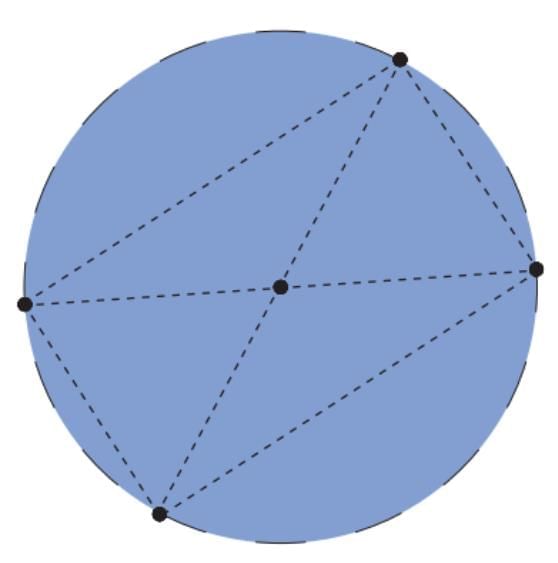 What shape is formed? Check the sides of the quadrilateral and the angles obtained.
What shape is formed? Check the sides of the quadrilateral and the angles obtained.
Try with a different pair of diameters.
What do you notice about the shape that is formed?
Is it possible to create a 4-sided shape other than a rectangle through this process?
Sol: What Shape is Formed?- When you join the four points, you get a quadrilateral ACBD.
- This quadrilateral is a rectangle (in some cases, a square if the diameters are perpendicular and equal divisions).
Checking the Sides:- Opposite sides are equal (AB = CD and AC = BD).
- The figure is symmetric about both diameters.
Checking the Angles:- Each interior angle is 90°.
- So the quadrilateral is a rectangle (and sometimes a square if the diameters are perpendicular).
Trying with Different Pairs of Diameters:- No matter which diameters you draw, the figure formed is always a rectangle (or a square).
- This is because diameters always pass through the centre, and opposite points on a circle are always symmetric.
Can a 4-sided Shape Other Than a Rectangle Be Formed? No.
- Any quadrilateral formed by joining the endpoints of two diameters of a circle will always be a rectangle (or a square as a special case).
- It cannot be any other quadrilateral like a trapezium, parallelogram (non-rectangle), or rhombus.
Cube
- A cube is a 3D shape with 6 square faces (flat surfaces).
- All the faces of a cube are equal in size and shape, and all angles are 90°.
- A cube has 12 edges (the sides where two faces meet) and 8 vertices (corners where edges meet).
- The length, width, and height of a cube are all the same, making it a regular shape.
- A cube is like a box—you can think of dice as an example of a cube.
- Surface Area of a cube is the area of all 6 faces added together.
- Volume of a cube is found by multiplying the length, width, and height (since all are equal, it's simply side³).
Cube Connections
Here are some big, solid cube frames. How many small cubes have been removed from each cube?
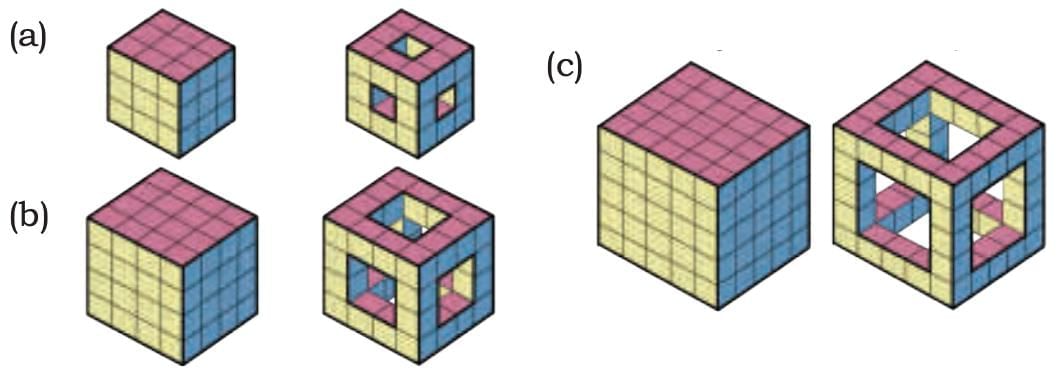
Sol: (a) First set- The cube is 4 × 4 × 4.
- Total small cubes = 64.
- From each face, 1 cube is removed from the centre.
- There are 6 faces, so 6 cubes are removed.
(b) Second set- The cube is 6 × 6 × 6.
- Total small cubes = 216.
- From each face, 4 cubes are removed (a 2 × 2 square in the centre).
- 6 faces × 4 cubes = 24 cubes removed.
(c) Third set- The cube is 8 × 8 × 8.
- Total small cubes = 512.
- From each face, 16 cubes are removed (a 4 × 4 square in the centre).
- 6 faces × 16 cubes = 96 cubes removed.
Icosahedron and Dodecahedron
- An icosahedron is a 3D shape with 20 triangular faces. All its faces are equilateral triangles, meaning all sides are equal.
- A dodecahedron is a 3D shape with 12 pentagonal faces. Each of its faces is a regular pentagon, meaning all sides and angles are equal.
- Both icosahedron and dodecahedron are types of Platonic solids, which means their faces are made up of identical regular polygons.
- An icosahedron has 30 edges and 12 vertices.
- A dodecahedron has 30 edges and 20 vertices.
- These shapes can be made by folding a 2D net into a 3D solid, and they have a special symmetry in geometry.
Let us find out
Use the nets provided at the end of the book to make icosahedron and dodecahedron models.
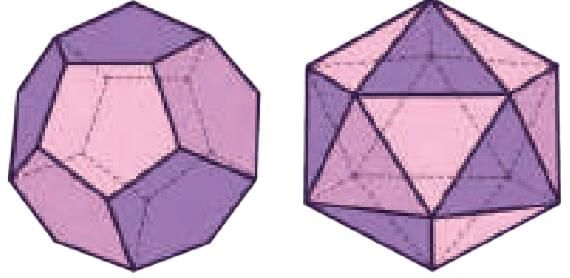
1. What shapes do you see in an icosahedron and a dodecahedron?
Icosahedron: ........ Dodecahedron: ........
2. Do all the faces look the same?
Icosahedron: ........ Dodecahedron: ........
3. How many faces meet at a vertex (point)?
Icosahedron: ........ Dodecahedron: ........
4. Do the same number of faces meet at each vertex?
Icosahedron: ........ Dodecahedron: ........
5. How many edges do you see?
Icosahedron: ........ Dodecahedron: ........
Sol:
1. Icosahedron: Triangles
Dodecahedron: Pentagons
2. Icosahedron: Yes
Dodecahedron: Yes
3. Icosahedron: 5
Dodecahedron: 3
4. Icosahedron: Yes
Dodecahedron: Yes
5. Icosahedron: 30
Dodecahedron: 30
How did you count them such that you do not miss out any edge or count an edge twice?
Sol: I counted by looking at one face at a time and then checking how many new edges appeared as I moved around the shape. I also remembered that every edge belongs to exactly two faces, so I did not count the same edge twice.
Can you think of any other solid shapes that have faces that look the same?
Sol: Yes. A cube has 6 square faces that are all the same. A tetrahedron has 4 triangular faces that are all the same. An octahedron has 8 triangular faces that are all the same.
Do the same number of faces meet at each common vertex?
Sol: Yes. In both the icosahedron and the dodecahedron, the same number of faces meet at every vertex. That is why they are called regular solids.
You can also build some 3-D shapes using straws or ice-cream sticks and clay or play-dough. Which shapes did you make?
Sol: I made a cube, a triangular prism, and a pyramid using straws and clay.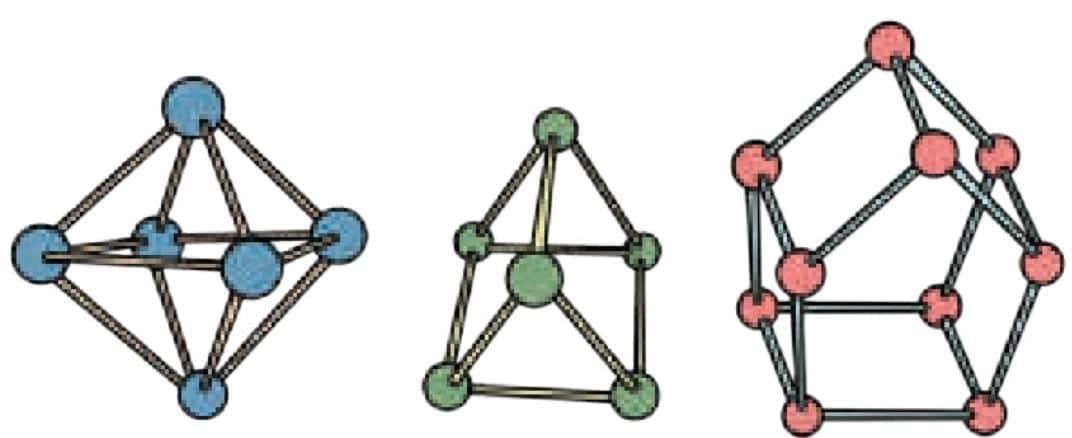
 What shape is formed? Check the sides of the quadrilateral and the angles obtained.
What shape is formed? Check the sides of the quadrilateral and the angles obtained. 
























 (a) How are they the same or different from each other?
(a) How are they the same or different from each other?
 You have a kite shape! What shapes do you see in the kite
You have a kite shape! What shapes do you see in the kite






















